《Keras深度学习：入门、实战与进阶》之回归问题实例：波士顿房价预测

news2024/9/20 17:54:39

本文摘自《Keras深度学习：入门、实战与进阶》。
在这里插入图片描述

本节将要预测20世纪70年代中期波士顿郊区房屋价格的中位数。这个数据是1978年统计收集的，数据集中的每一行数据都是对波士顿周边或城镇房价的描述，包含以下14个特征和506条数据。
 CRIM：城镇人均犯罪率。
 ZN：住宅用地所占比例。
 INDUS：城镇中非住宅用地所占比例。
 CHAS：虚拟变量，用于回归分析。
 NOX：环保指数。
 RM：每栋住宅的房间数。
 AGE：1940年以前建成的自住单位的比例。
 DIS：距离5个波士顿的就业中心的加权距离。
 RAD：距离高速公路的便利指数。
 TAX：每一万美元的不动产税率。
 PTRATIO：城镇中教师和学生的比例。
 B：城镇中黑人的比例。
 LSTAT：地区中有多少房东属于低收入人群。
 MEDV：自住房屋房价中位数。
通过Keras API把波士顿房屋价格数据集导入到R中，并查看测试集和训练集的样本数量。

> library(keras)
> # 1. 导入数据
> boston_housing <- dataset_boston_housing()
> c(train_data, train_labels) %<-% boston_housing$train
> c(test_data, test_labels) %<-% boston_housing$test
> cat('训练样本数量:',length(train_labels),'\n',
+     '测试样本数量:',length(test_labels))
训练样本数量: 404 
测试样本数量: 102

这个数据集比MNIST数据集小很多：它一共有506个样本，分为404个训练样本和102个测试样本。
在对数据集做缺失值插补和特征预处理之前，让我们观察训练集中各列数据的描述统计分析。skimr软件包提供了一个很好的解决方案，可以显示每列的关键描述统计信息。skim()函数会生成包含每一列的描述统计的数据框，并包含一个直方图，可以直观查看数值变量的数据分布情况。

> # 添加列名称
> library(tibble)
> column_names <- c('CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 
+                   'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT')
> train_df <- as_tibble(train_data)
> colnames(train_df) <- column_names
> # 对数据进行描述统计分析
> if(!require(skimr)) install.packages("skimr")
> skimmed <- skim(train_df)
> skimmed

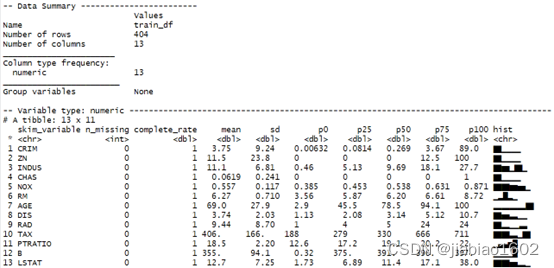
在这里插入图片描述
train_data一共有404行13列，13列均为数值变量，最后一部分是各数值变量的描述统计分析。n_missing是统计各变量的样本缺失数量，此数据各变量均为0，说明无数据缺失；complete_rate是数据完整度，此数据各变量均为1；mean、sd、p0、p25、p50、p75、p100依次为均值、标准差、最小值、第一四分位数、中位数、第三四分位数、最大值统计指标，可见各变量间存在尺度不一致情况，需要在建模前进行数据标准化处理；最后一列是数据分布的直方图可视化展示。
从描述统计分析结果可知，输入变量中的各列数据范围差异比较大。在建模前，需先对数据集进行标准化处理。此案例使用scale()函数进行Z-Score标准化，处理后训练集中各列数据符合标准正态分布，即均值为0，标准差为1。

> # 对train_data进行标准化
> train_data <- scale(train_data)

接着使用对训练集标准化后得到的各列均值和标准差对测试集数据进行数据处理。

> col_means_train <- attr(train_data, "scaled:center") 
> col_stddevs_train <- attr(train_data, "scaled:scale")
> test_data <- scale(test_data, center = col_means_train, scale = col_stddevs_train)

最后，将标准化后的因变量和自变量进行合并，形成包含标签的训练及测试数据集。

> all_train_data=cbind(train_data,train_labels)
> all_test_data=cbind(test_data,test_labels)
> all_train_data=as.data.frame(all_train_data)
> all_test_data=as.data.frame(all_test_data)
> colnames(all_train_data) <- c(column_names,'MEDV')
> colnames(all_test_data) <- c(column_names,'MEDV')

经过上一小结的数据预处理，训练集和测试集已经达到深度学习建模要求。本小节将利用全连接神经网络进行模型构建、模型训练及模型预测等工作。
让我们建立一个序贯模型，该模型具有两个全连接的隐藏层，神经元数量均为64，采用ReLU激活函数。因为这是一个回归问题，不需要将预测结果进行分类转换，所以输出层不设置激活函数，直接输出数值。
模型定义完成后，需要对模型进行编译，编译模型是为了使模型能够有效地使用Keras封装的数值计算。Keras可以根据后端自动选择最佳方式来训练模型，并进行预测。编译时，必须指定训练模型时所需的一些属性。训练一个神经网络模型，意味着找到最好的权重集来对这个问题作出预测。
编译模型时，必须指定用于评估一组权重的损失函数（loss）、用于搜索网络不同权重的优化器（optimizer），以及希望在模型训练期间收集和报告的可选指标。在这个例子中，采用Adam优化器，均方误差（MSE）作为损失函数。同时采用平均绝对误差（MAE）来评估模型的性能，值越小代表模型的性能越好。

> # 构建模型函数
> build_model <- function() {
+   
+   model <- keras_model_sequential() %>%
+     layer_dense(units = 64, activation = "relu",
+                 input_shape = dim(train_data)[2]) %>%
+     layer_dense(units = 64, activation = "relu") %>%
+     layer_dense(units = 1)
+   
+   model %>% compile(
+     loss = "mse",
+     optimizer = optimizer_rmsprop(),
+     metrics = list("mean_absolute_error")
+   )
+   
+   model
+ }

模型编译完成后，就可以用于计算了。在使用模型预测新数据前，需要先对模型进行训练。模型通过调用fit方法来实现。训练过程将采用epochs参数，对数据集进行固定次数的迭代，因此必须指定epochs参数大小进行模型训练，还需要设置在执行神经网络中的权重更新的每个批次中所用实例的个数（batch_size，默认为32）。
在这个例子中，将运行一个较小的epochs参数150，batch_size使用默认的32，且我们设置一个回调函数，如果经过20次训练周期后验证集的损失函数没有明显改善，将自动停止训练。

> # 设置回调函数的停止条件
> early_stop <- callback_early_stopping(monitor = "val_loss", patience = 20)
> # 训练模型
> mlp_model <- build_model()
> history <- mlp_model %>% fit(
+   train_data,
+   train_labels,
+   epochs = 150, 
+   validation_split = 0.2,
+   verbose = 0,
+   callbacks = early_stop
+ )
> plot(history)

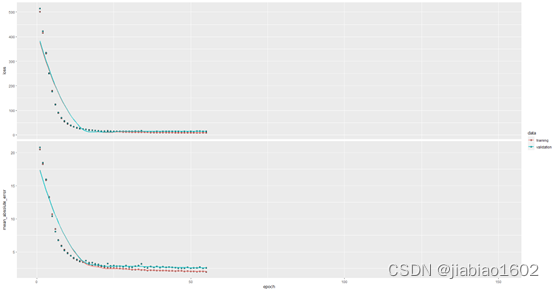
在这里插入图片描述
模型在经过50多次训练周期后停止了训练。通过以下命令可以查看模型的训练周期。

> cat('模型训练周期的次数为：','\n',length(history$metrics$val_loss))
模型训练周期的次数为： 
 55

利用callback_early_stopping回调函数后，训练模型在55次训练周期后停止了训练。因为模型的验证集的损失函数值在最后20次的训练周期均没有再改善，所以停止训练。
因为回调函数参数min_delta默认值为0，所以当出现训练周期为35时的验证集的损失函数值均大于后面20次训练周期的验证集的损失函数值，模型停止训练。以下代码查看当训练周期为35时的验证集损失函数值，并计算最后20次训练周期与其的差值。

> cat('epoch为35时的验证集损失函数值：','\n',
+     history$metrics$val_loss[35])
epoch为35时的验证集损失函数值： 
 13.57665
> diff <- history$metrics$val_loss[36:55] - history$metrics$val_loss[35]
> round(diff,1)
 [1] 0.1 0.4 0.0 1.0 0.1 0.7 0.6 1.0 0.8 1.4 0.9 0.0 0.7 0.1 0.6 0.4 1.8 2.2 0.7 1.1

因为回调函数参数restore_best_weights默认值为FALSE, 则模型将会使用在训练的最后一步获得的权重值。
最后，利用训练好的模型对测试样本的房价进行预测，并计算与实际值的平均绝对误差值（MAE）。

> # 对测试样本进行预测
> test_predictions <- mlp_model %>% 
+   predict(test_data)
> # 查看平均绝对误差
> mae <- mean(abs(all_test_data$MEDV-test_predictions))
> paste0('测试集上的平均绝对误差: $',
+        sprintf("%.f", mae * 1000))
[1] "测试集上的平均绝对误差: $3043"