2023.2.3
CNN中出现一些新的概念:填充、步幅 等,此外各层中传递的数据是有形状的,与之前的全连接层神经网络完全不同;
一、全连接层存在的问题:
全连接层神经网络使用了Affine层,在相邻的神经元全部连接在一起,输出数量可以自己任意决定;
就是这样的结构导致数据的形状被忽略了,图像通常是(通道,高,长)的3维数据,比如MNIST数据集图像,通常是(1,28,28),但是在全连接神经网络中却被排列成(1,784)的形状作为输入。
3维图像,这个形状中应该含有重要的空间信息。比如,空间上临近的像素为相似的值、RGB的各个通道之间分别有密切的关联性、相距较远的像素之间关联等,3维形状中可能隐匿有值提取的本质模式。但是,因为全连接层对于这样的“忽略”,将全部输入数据作为相同的神经元(同一维度的神经元)处理,所以无法使用与形状相关的信息。
CNN中,有时将卷积层的输入输出数据称为 特征图 。 其中,卷积层输入被称为 输入特征图,卷积层输出 称为 输出特征图。
二、卷积运算:
卷积层处理的就是卷积运算。卷积运算相当于图像处理中的“滤波器运算”。(滤波器也被称为 卷积核)
例子:卷积运算图例,来源于教材;

对于输入数据,卷积运算以一定的间隔划定滤波器的窗口并应用。这里所说的窗口时指例子中3×3的灰色部分。如图将各个位置的 卷积核 和输入的对应元素相乘,然后在求和(有时将这个计算称为 乘积累加运算)。然后,将这个结果保存到输出的对应位置。将这过程所有位置都进行一遍,就能得到卷积运算的输出。
在全连接神经网络中,除了权重参数,还存在偏置。CNN中,滤波器的参数就对应之前的权重,也存在偏置。(图例来源于教材)

向滤波器中加上偏置,这个值也会加到滤波器的其他元素上。
三、填充:
在进行卷积层处理之前,有时要向输入数据的周围填入固定的数据(比如 0),这称为 填充 (Padding)。
上个图例中,填充值为0,所以大小为4×4的图像与3×3的卷积核进行卷积运算,得到的输出特征图的大小是2×2。
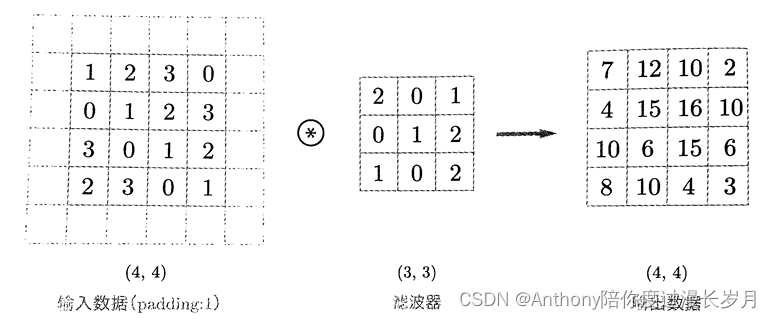
而现在填充值为1,4×4的图像与3×3的卷积核进行卷积运算,得到的输出特征图的大小是4×4.
所以,使用填充的主要目的是为了调整输出大小。这在进行重复地多次地卷积运算的深度网络中也是一个问题。如果填充值为0,每次卷积运算都会压缩空间,那么到某个时候输出大小就有可能变为1,导致无法在应用卷积运算。为了避免出现这样的情况,就要使用填充,将保持空间大小不变的情况下将数据传递给下一层。
四、步幅:
应用滤波器(卷积核)的位置间隔为 步幅 (Stride)。
之前的例子的步幅是都是1,如果将步幅设置为2,则应用滤波器的窗口间隔为2,例子来源于教材;

对输入大小为(7×7)的数据,以步幅为2应用滤波器,输出大小为(3×3)
可以观察到,增大步幅后,输出大小会变小。而增大填充后,输出大小会保存或者变大。
用公式表达:假设输入大小为(H,W),滤波器(卷积核)的大小为(FH,FW),输出大小为(OH,OF);
当OH和OW的值无法除尽时,需要采取相应报错对策,有时因为不同的深度学习神经网络,回想最接近的整数四舍五入,不进行报错二继续学习;
五、3维数据的卷积运算:
2维形状是(高,长),3维形状是(通道,高,长)
通道方向上有多个特征图,会按通道进行输入数据和滤波器的卷积运算,并将结构相加,从而得到输出。
例子:(来源于教材)

但是,需要注意的是,在3维数据的卷积运算中,输入数据和滤波器的通道数要设置成相同的值。
六、结合方块思考:
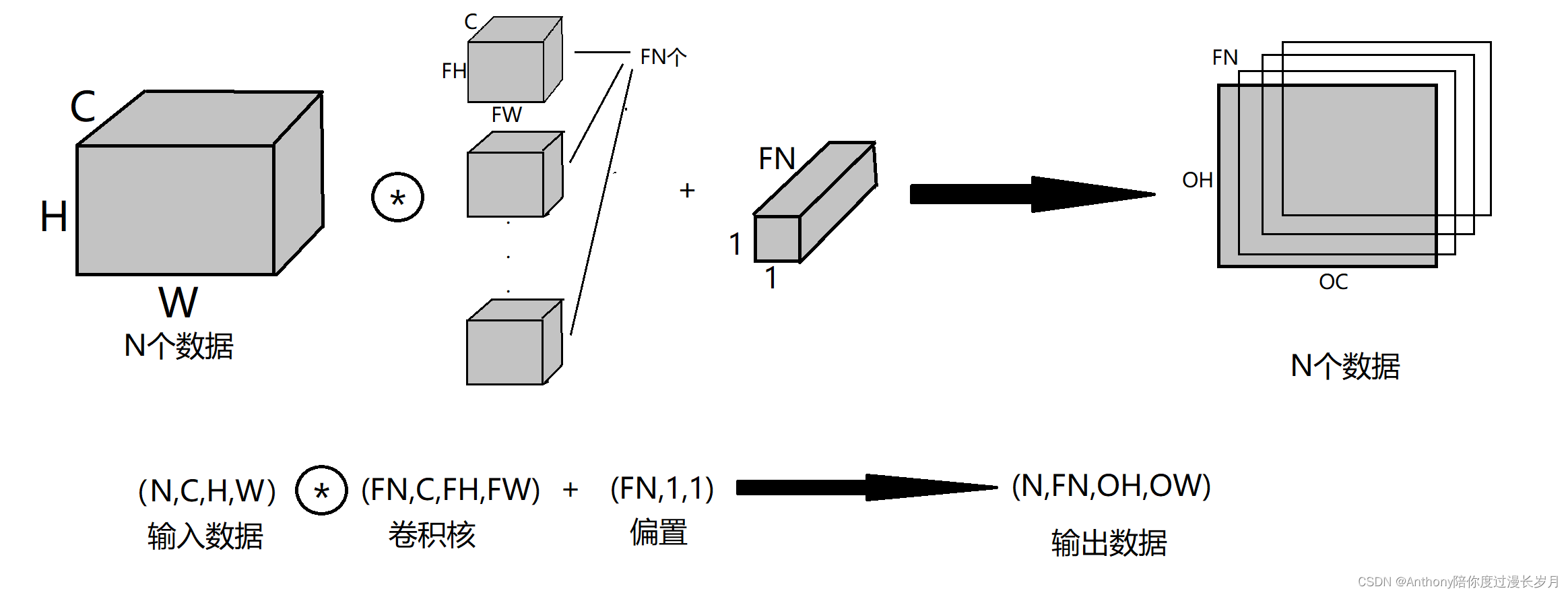
将数据和滤波器比作长方体来考虑3维卷积;(channel,height,width)→(c,h,w)

像这个例子输出的是一张特征图,n个卷积核就会输出n张特征图,

输入数据通过FN个滤波器以后,输出的特征图也变成了FN个。如果将这FN个特征图汇集在一起,就可以得到形状为(FN,OH,OW)的“方块”,他传递给下一层就是CNN的处理流。
有关于卷积运算,我们也要考虑滤波器(卷积核)的数量,比如写作(output_channel,input_channel,height,width)的书写顺序。
卷积运算核全连接层一样存在偏置:

这里的偏置的形状是(FN,1,1)最后的输出数据也要加上偏置值。另外,不同形状的方块相加时,可以基于Numpy的广播功能轻松实现。
七、批处理:
神经网络的推理处理中,进行了将数据打包的批处理,之前的全连接层神经网络的实现也使用了批处理,通过批处理,还能实现按粗粒高效化和学习时对mini-batch的对应;
同理,卷积运算也能够进行对应的批处理。为此,需要将各层传递的数据保存成4维数据。
保存形式(形状):(batch_num,channel,height,width)的顺序保存数据。
如图将N个数据进行卷积运算,批处理将N次的处理汇总成1次进行;