从零开始的数模（十一）微分方程建模

news2024/11/10 23:11:31

目录

一、概念

1.1什么是微分方程建模

1.2使用场合

二、基于python的微分方程建模

2.1scipy.integrate.odeint() 函数

​编辑2.2案例

​编辑

三、基于MATLAB的微分方程建模

四、偏微分方程的求解

一、概念

1.1什么是微分方程建模


微分方程建模是数学模型的重要方法，因为许多实际问题的数学描述将导致求解微分方程的定解问题。所以微分方程求解就显得格外重要啦。

如何把实际问题转化为微分方程呢？
1.根据诗级要求确定要研究的晾（自变量、未知函数、必要的参数等）并且确定坐标系。
2.找出这些量所满足的基本规律（物理的、几何的、化学的或者生物学的）。
3.运用这些规律列出方程和定解条件。

列方程的方式
1.按规律直接列方程。
2.微元分析法与任意区域上取积分的方法。
3.模拟近似法。

1.2使用场合

1.2.1

例题

1.2.2例题2

 

1.2.3

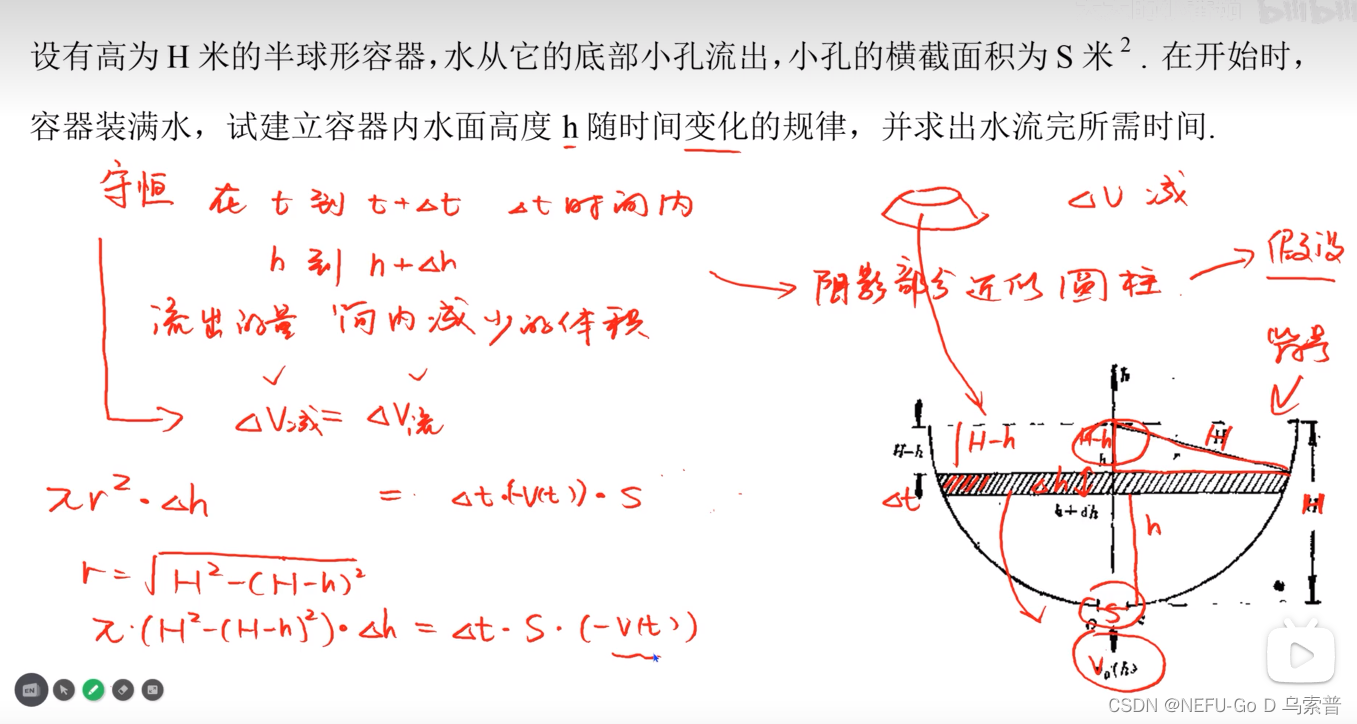
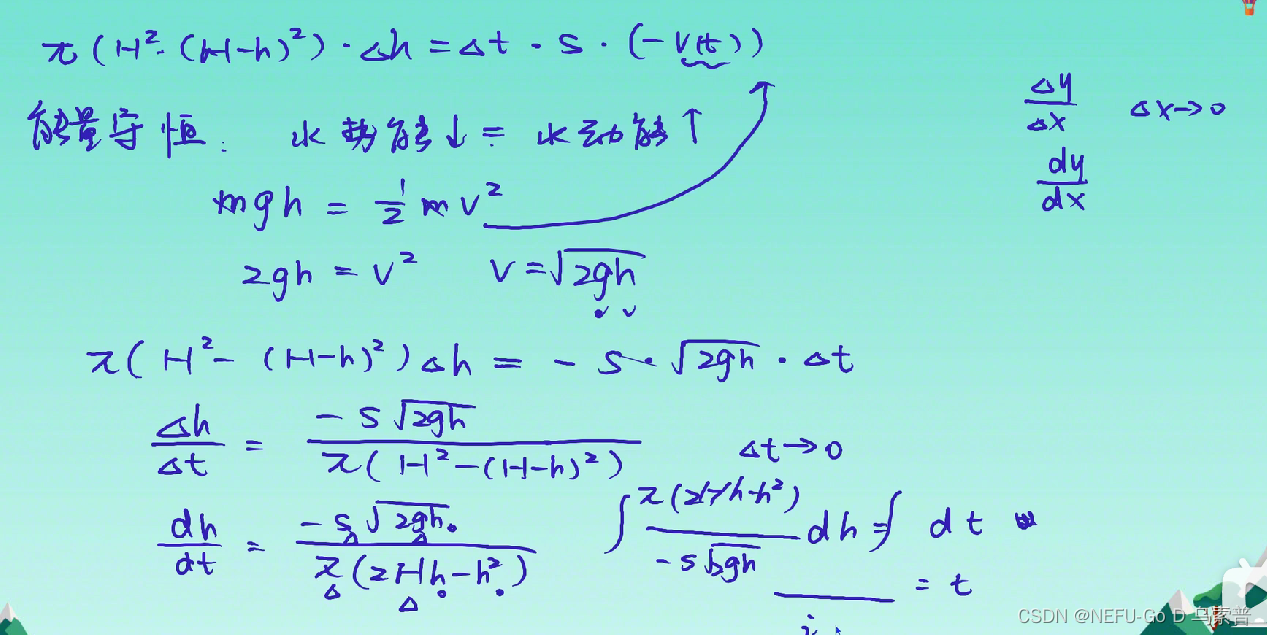 1.2.4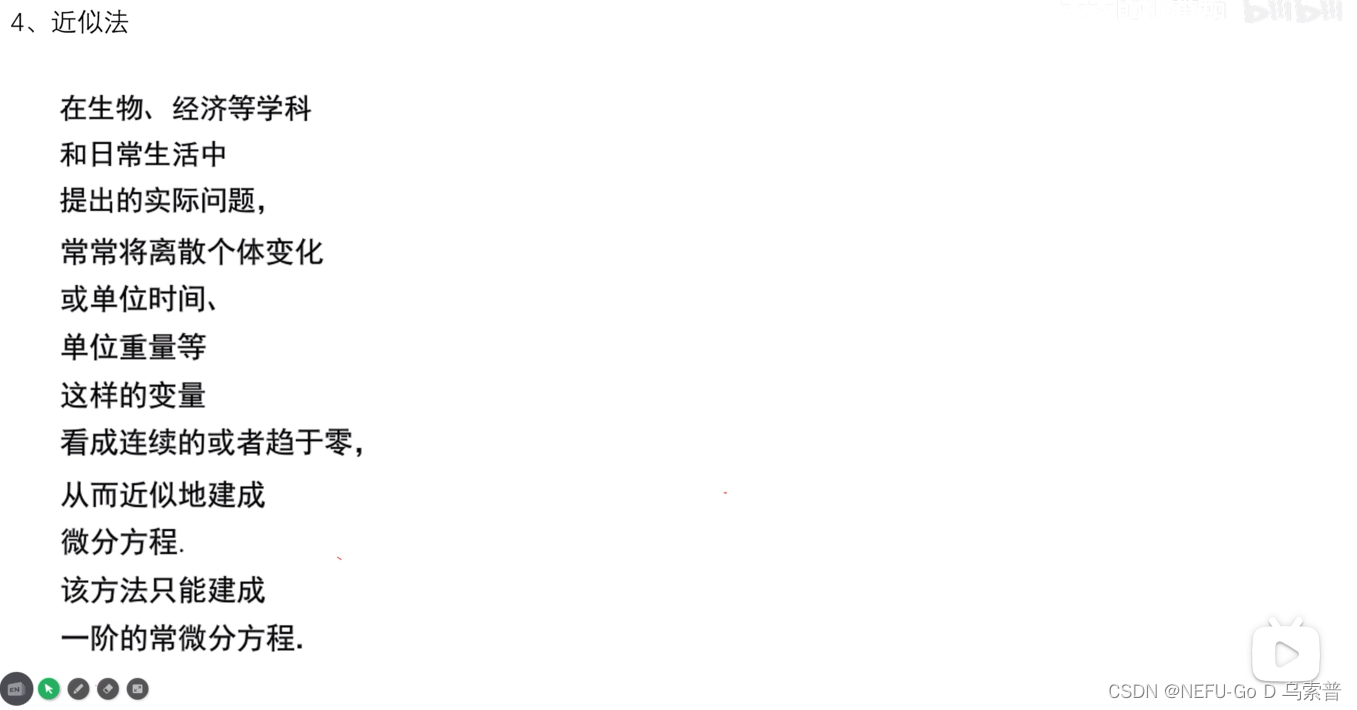

二、基于python的微分方程建模

我们的选择是 Python 常用工具包三剑客：Scipy、Numpy 和 Matplotlib：

Scipy 是 Python 算法库和数学工具包，包括最优化、线性代数、积分、插值、特殊函数、傅里叶变换、信号和图像处理、常微分方程求解等模块。有人介绍 Scipy 就是 Python 语言的 Matlab，所以大部分数学建模问题都可以用它搞定。
Numpy 提供了高维数组的实现与计算的功能，如线性代数运算、傅里叶变换及随机数生成，另外还提供了与 C/C++ 等语言的集成工具。
Matplotlib 是可视化工具包，可以方便地绘制各种数据可视化图表，如折线图、散点图、直方图、条形图、箱形图、饼图、三维图，等等。
顺便说一句，还有一个 Python 符号运算工具包 SymPy，以解析方式求解积分、微分方程，也就是说给出的结果是微分方程的解析解表达式。很牛，但只能求解有解析解的微分方程，所以，你知道就可以了。

2.1scipy.integrate.odeint() 函数

SciPy 提供了两种方式求解常微分方程：基于 odeint 函数的 API 比较简单易学，基于 ode 类的面向对象的 API 更加灵活。

scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)

 

odeint 的主要参数：

求解标准形式的微分方程（组）主要使用前三个参数：

2.2案例

 

# 1. 求解微分方程初值问题(scipy.integrate.odeint)
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt

def dy_dt(y, t):  # 定义函数 f(y,t)
    return np.sin(t**2)

y0 = [1]  # y0 = 1 也可以
t = np.arange(-10,10,0.01)  # (start,stop,step)
y = odeint(dy_dt, y0, t)  # 求解微分方程初值问题

# 绘图
plt.plot(t, y)
plt.title("scipy.integrate.odeint")
plt.show()

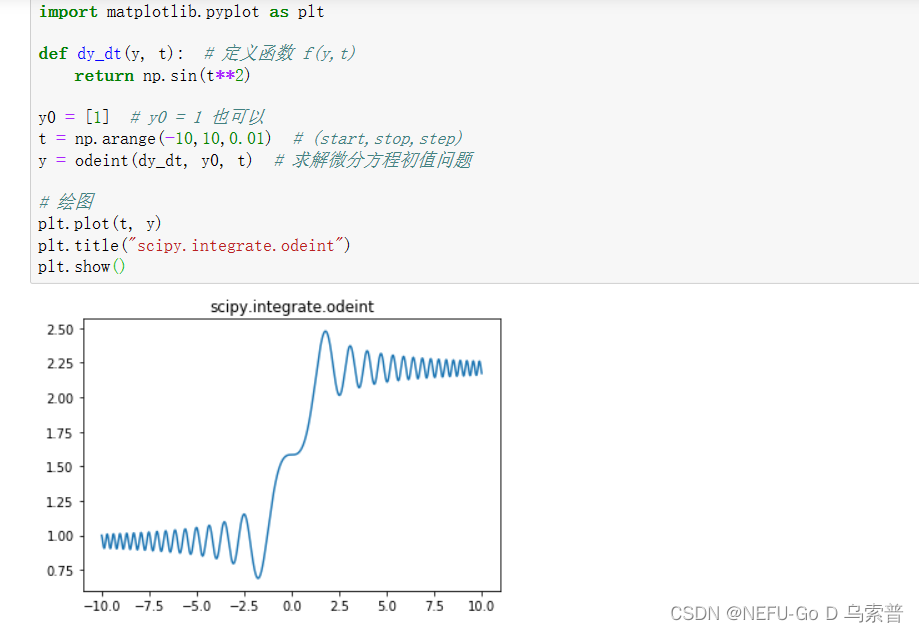
 案例2：Scipy 求解一阶常微分方程组

# 2. 求解微分方程组初值问题(scipy.integrate.odeint)
from scipy.integrate import odeint    # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 导数函数, 求 W=[x,y,z] 点的导数 dW/dt
def lorenz(W,t,p,r,b):  # by youcans
    x, y, z = W  # W=[x,y,z]
    dx_dt = p*(y-x)  # dx/dt = p*(y-x), p: sigma
    dy_dt = x*(r-z) - y  # dy/dt = x*(r-z)-y, r:rho
    dz_dt = x*y - b*z  # dz/dt = x*y - b*z, b;beta
    return np.array([dx_dt,dy_dt,dz_dt])

t = np.arange(0, 30, 0.01)  # 创建时间点 (start,stop,step)
paras = (10.0, 28.0, 3.0)  # 设置 Lorenz 方程中的参数 (p,r,b)

# 调用ode对lorenz进行求解, 用两个不同的初始值 W1、W2 分别求解
W1 = (0.0, 1.00, 0.0)  # 定义初值为 W1
track1 = odeint(lorenz, W1, t, args=(10.0, 28.0, 3.0))  # args 设置导数函数的参数
W2 = (0.0, 1.01, 0.0)  # 定义初值为 W2
track2 = odeint(lorenz, W2, t, args=paras)  # 通过 paras 传递导数函数的参数

# 绘图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2], color='magenta') # 绘制轨迹 1
ax.plot(track2[:,0], track2[:,1], track2[:,2], color='deepskyblue') # 绘制轨迹 2
ax.set_title("Lorenz attractor by scipy.integrate.odeint")
plt.show()

 案例3：Scipy 求解高阶常微分方程

# 3. 求解二阶微分方程初值问题(scipy.integrate.odeint)
# Second ODE by scipy.integrate.odeint
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt

# 导数函数，求 Y=[u,v] 点的导数 dY/dt
def deriv(Y, t, a, w):
    u, v = Y  # Y=[u,v]
    dY_dt = [v, -2*a*v-w*w*u]
    return dY_dt

t = np.arange(0, 20, 0.01)  # 创建时间点 (start,stop,step)
# 设置导数函数中的参数 (a, w)
paras1 = (1, 0.6)  # 过阻尼：a^2 - w^2 > 0
paras2 = (1, 1)  # 临界阻尼：a^2 - w^2 = 0
paras3 = (0.3, 1)  # 欠阻尼：a^2 - w^2 < 0

# 调用ode对进行求解, 用两个不同的初始值 W1、W2 分别求解
Y0 = (1.0, 0.0)  # 定义初值为 Y0=[u0,v0]
Y1 = odeint(deriv, Y0, t, args=paras1)  # args 设置导数函数的参数
Y2 = odeint(deriv, Y0, t, args=paras2)  # args 设置导数函数的参数
Y3 = odeint(deriv, Y0, t, args=paras3)  # args 设置导数函数的参数
# W2 = (0.0, 1.01, 0.0)  # 定义初值为 W2
# track2 = odeint(lorenz, W2, t, args=paras)  # 通过 paras 传递导数函数的参数

# 绘图
plt.plot(t, Y1[:, 0], 'r-', label='u1(t)')
plt.plot(t, Y2[:, 0], 'b-', label='u2(t)')
plt.plot(t, Y3[:, 0], 'g-', label='u3(t)')
plt.plot(t, Y1[:, 1], 'r:', label='v1(t)')
plt.plot(t, Y2[:, 1], 'b:', label='v2(t)')
plt.plot(t, Y3[:, 1], 'g:', label='v3(t)')
plt.axis([0, 20, -0.8, 1.2])
plt.legend(loc='best')
plt.title("Second ODE by scipy.integrate.odeint")
plt.show()

案例四求微分方程的通解

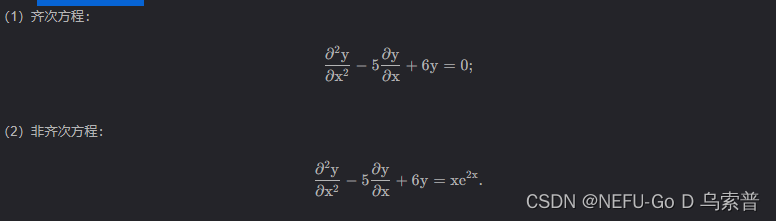
from sympy import *

x = symbols('x'); y = symbols('y',cls=Function)
eq1 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)
eq2 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)-x*exp(2*x)
print("齐次方程的解为：",dsolve(eq1,y(x)))
print("非齐次方程的解为：",dsolve(eq2,y(x)))

 案例五

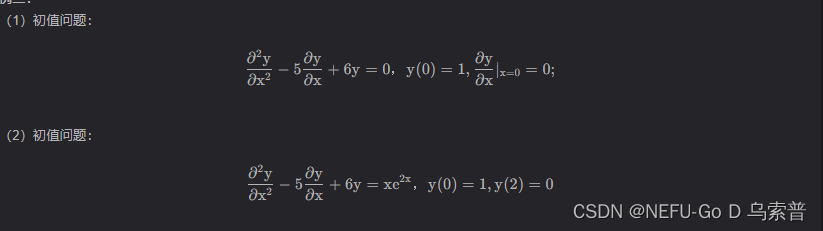
from sympy import *

x = symbols('x'); y = symbols('y',cls=Function)
eq1 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)
eq2 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)-x*exp(2*x)
print("初值问题的解为：{}".format(dsolve(eq1,y(x),ics={y(0):1,diff(y(x),x).subs(x,0):0})))
y2 = dsolve(eq2,y(x),ics={y(0):1,y(2):0})
print("边值问题的解为：{}".format(y2))

案例六

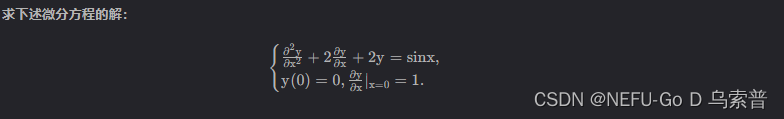
from sympy.abc import x
from sympy import Function, diff, dsolve, sin

y = Function('y')
eq = diff(y(x),x,2)+2*diff(y(x),x)+2*y(x)-sin(x)  # 定义方程
con = {y(0): 0,diff(y(x), x).subs(x,0): 1}        # 定义初值条件
y = dsolve(eq, ics=con)
print(y)

 案例七求下述微分方程的解：

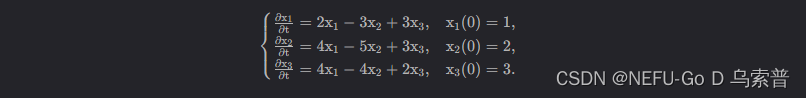
import sympy as sp

t = sp.symbols('t')
x1,x2,x3 = sp.symbols('x1,x2,x3', cls=sp.Function)
eq = [x1(t).diff(t)-2*x1(t)+3*x2(t)-3*x3(t),
      x2(t).diff(t)-4*x1(t)+5*x2(t)-3*x3(t),
      x3(t).diff(t)-4*x1(t)+4*x2(t)-2*x3(t),
      ]
con = {x1(0):1, x2(0):2, x3(0):3}
s = sp.dsolve(eq,ics=con)
print(s)

案例八


from matplotlib.font_manager import FontProperties
from scipy.integrate import odeint
from sympy.abc import t
import numpy as np
import matplotlib.pyplot as plt

my_font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)

def Pfun(y, x):
    y1,y2 = y;
    return np.array([y2, -2*y1-2*y2])
x = np.arange(0, 10, 1.0)              # 创建时间点
sol1 = odeint(Pfun, [0.0, 1.0], x)     # 求数值解

plt.plot(x, sol1[:, 0],'r*',label="数值解")
plt.plot(x, np.exp(-x)*np.sin(x),'g', label="符号解曲线")
plt.legend(prop=my_font)  # 表示添加图例，并且用特有的 prop=my_font
plt.savefig("例八")
plt.show()

三、基于MATLAB的微分方程建模

人口模型

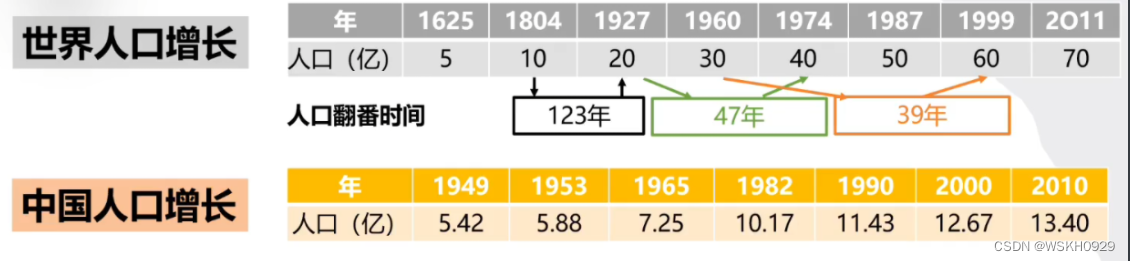
在这里插入图片描述

在这里插入图片描述

 Matlab代码：

% 人口增长-指数增长模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 250;
% 定义并初始化参数
x = zeros(1,n);
x(1,1) = 5.42; % 初始化人口数(亿)
r = 0.018; % 人口增长率
% 开始迭代
for t = 2:n
    x(1,t) = x(1,1)*exp(r*t);
end
% 绘图
plot(1:1:n,x);
legend('人口增长曲线');
xlabel('迭代次数');
ylabel('人口数（亿） ');
grid on;

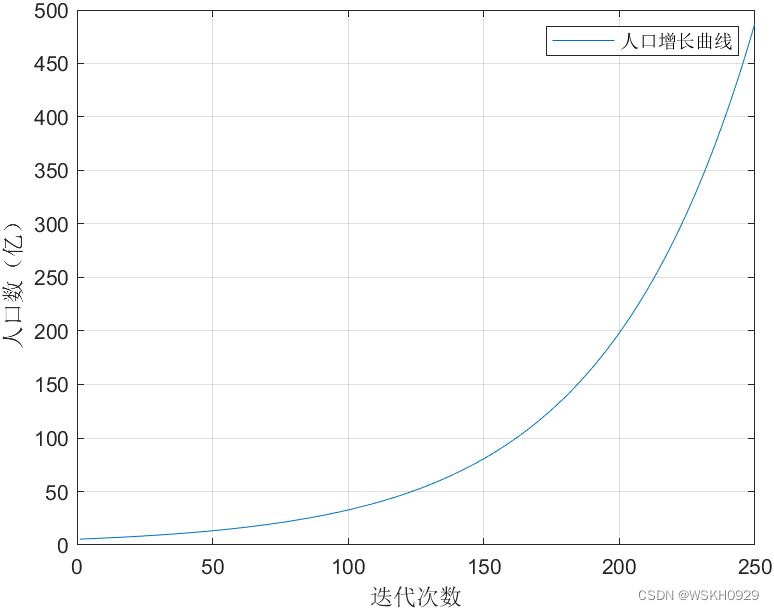
在这里插入图片描述

 

 

% 人口增长-阻滞增长模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 500;
% 定义并初始化参数
x = zeros(1,n);
x(1,1) = 5.42; % 初始化人口数(亿)
r = 0.018; % 初始人口增长率
xm = 100; % 最大人口数
% 开始迭代
for t = 2:n
    x(1,t) = xm/(1+(xm/x(1,1)-1)*exp(-r*t));
end
% 绘图
plot(1:1:n,x);
legend('人口增长曲线');
xlabel('迭代次数');
ylabel('人口数（亿） ');
grid on;

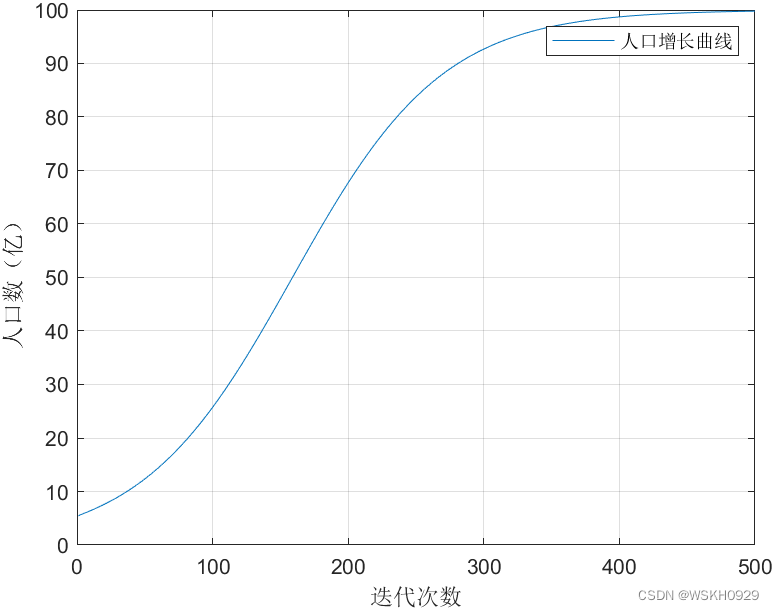
在这里插入图片描述

 

% 传染病SI模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 100;
% 定义并初始化状态E(s,i)
E = zeros(2,n);
E(1,1) = 0.99; % 初始健康者比例
E(2,1) = 0.01; % 初始感染者比例
% 初始化参数
L = 0.5; % 病人日接触率
% 开始迭代
for t = 1:n-1
    E(2,t+1) = E(2,t) + L*E(2,t)*(1-E(2,t));
    E(1,t+1) = 1 - E(2,t+1);
end
% 绘图
s = E(1,:); % 健康者比例数据
i = E(2,:); % 感染者比例数据
plot(s,'DisplayName','s');hold on;
plot(i,'DisplayName','i');
legend('健康者比例','感染者比例');
xlabel('迭代次数');
ylabel('比例');
grid on;
hold off;

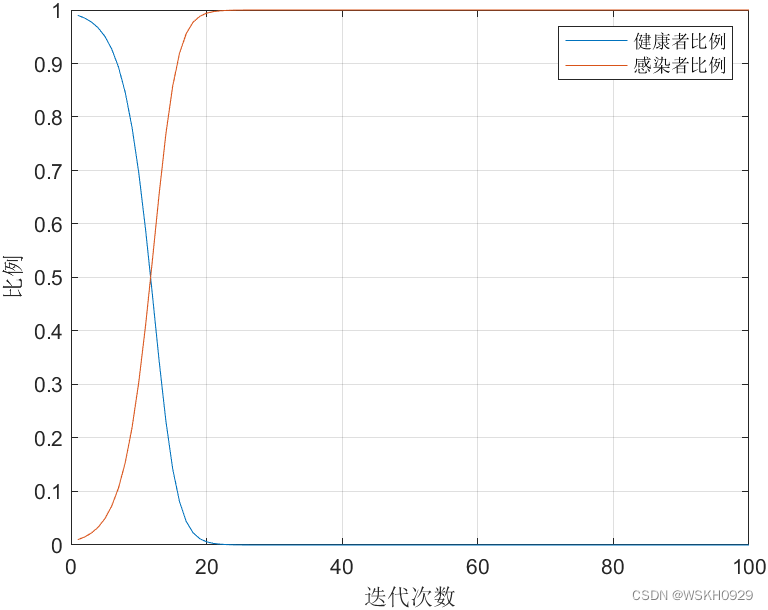
 在这里插入图片描述

SI模型的缺点在于，没有考虑病人可以被治愈的情况，导致最后所有健康者都会变为感染者，不太符合实际情况 

% 传染病SIS模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 100;
% 定义并初始化状态E(s,i)
E = zeros(2,n);
E(1,1) = 0.99; % 初始健康者比例
E(2,1) = 0.01; % 初始感染者比例
% 初始化参数
L = 0.5; % 病人日接触率
M = 0.2; % 病人日治愈率
% 开始迭代
for t = 1:n-1
    E(2,t+1) = E(2,t) + L*E(2,t)*(1-E(2,t))-M*E(2,t);
    E(1,t+1) = 1 - E(2,t+1);
end
% 绘图
s = E(1,:); % 健康者比例数据
i = E(2,:); % 感染者比例数据
plot(s,'DisplayName','s');hold on;
plot(i,'DisplayName','i');
legend('健康者比例','感染者比例');
xlabel('迭代次数');
ylabel('比例');
grid on;
hold off;

在这里插入图片描述

SIS模型作为SI模型的升级版，考虑了病人被治愈的情况，但同时，SIS模型没有考虑病人被治愈后，可能会产生抗体，而不会被再次感染的情况，不太符合某些传染病的模拟

% 传染病SIR模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 100;
% 定义并初始化状态E(s,i,r)
E = zeros(3,n);
E(1,1) = 0.99; % 初始健康者比例
E(2,1) = 0.01; % 初始感染者比例
E(3,1) = 1 - E(1,1) - E(2,1); % 初始免疫者比例(假设一开始没有免疫者)
% 初始化参数
L = 0.5; % 病人日接触率
M = 0.1; % 日治愈率
% 开始迭代
for t = 1:n-1
    E(1,t+1) = E(1,t) - L*E(1,t)*E(2,t);
    E(2,t+1) = E(2,t) + L*E(1,t)*E(2,t) - M*E(2,t);
    E(3,t+1) = 1 - E(1,t+1) - E(2,t+1);
end
% 绘图
s = E(1,:); % 健康者比例数据
i = E(2,:); % 感染者比例数据
r = E(3,:); % 免疫者比例数据
plot(s,'DisplayName','s');hold on;
plot(i,'DisplayName','i');
plot(r,'DisplayName','r');
legend('健康者比例','感染者比例','免疫者比例');
xlabel('迭代次数');
ylabel('比例');
grid on;
hold off;

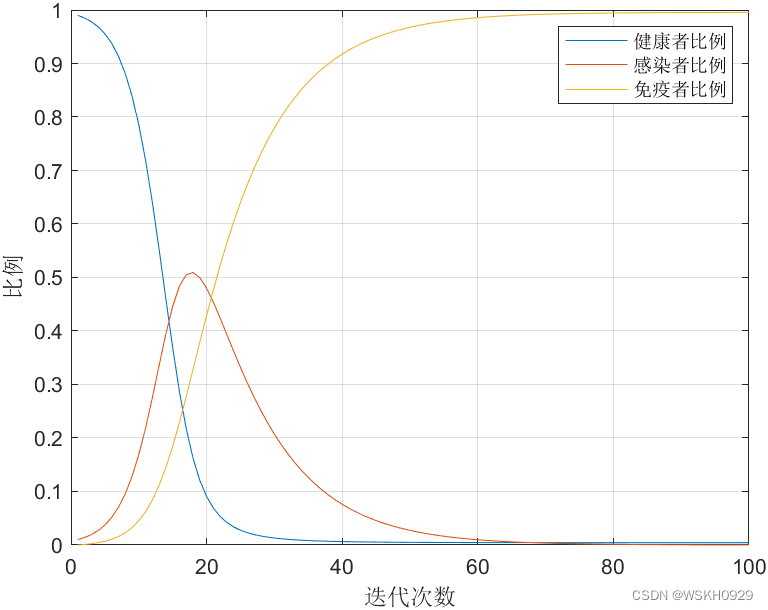
在这里插入图片描述

可以看到，在SIR模型中，随着时间的推移，感染者人数先上升，达到一个峰值后，再下降，最后下降为0，所有人都成为免疫者

四、偏微分方程的求解

 例题

 

例题

 

 

 

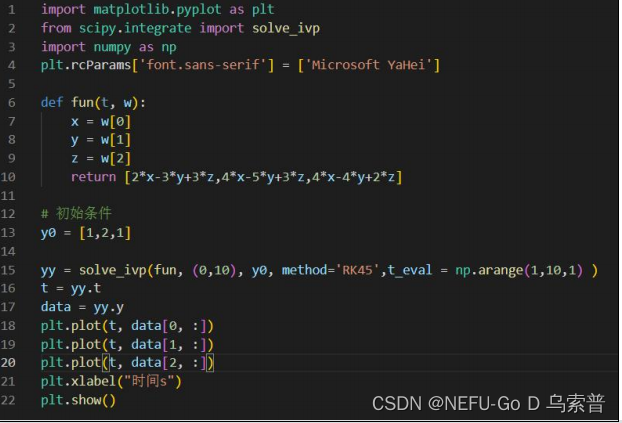
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
import numpy as np
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']

def fun(t, w):
    x = w[0]
    y = w[1]
    return [-x**3-y,-y**3+x]

# 初始条件
y0 = [1,0.5]

yy = solve_ivp(fun, (0,100), y0, method='RK45',t_eval = np.arange(0,100,1) )
t = yy.t
data = yy.y
plt.plot(t, data[0, :])
plt.plot(t, data[1, :])
plt.xlabel("时间s")
plt.show()

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/196883.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

AcWing 1081. 度的数量（数位DP）

AcWing 1081. 度的数量（数位DP）

AcWing 1081. 度的数量&#xff08;数位DP&#xff09;一、问题二 、数位DP三、解析1、题意理解2、题目分析三、代码一、问题 二 、数位DP 这道题是一道数位DP的题目&#xff0c;其实数位DP更像我们在高中阶段学过的排列组合问题中的分类讨论。 数位DP顾名思义就是按照数字的…
阅读更多...
B/S端界面控件DevExtreme v22.2新功能 - 如何在日历中显示周数？

B/S端界面控件DevExtreme v22.2新功能 - 如何在日历中显示周数？

DevExtreme拥有高性能的HTML5 / JavaScript小部件集合&#xff0c;使您可以利用现代Web开发堆栈&#xff08;包括React&#xff0c;Angular&#xff0c;ASP.NET Core&#xff0c;jQuery&#xff0c;Knockout等&#xff09;构建交互式的Web应用程序&#xff0c;该套件附带功能齐…
阅读更多...
LeetCode-1145. 二叉树着色游戏【深度优先搜索，二叉树】

LeetCode-1145. 二叉树着色游戏【深度优先搜索，二叉树】

LeetCode-1145. 二叉树着色游戏【深度优先搜索&#xff0c;二叉树】题目描述&#xff1a;解题思路一&#xff1a;深度优先搜索分别计算x的左子树lsz和右子树rsz的节点个数。那么除去x与其左右子树的父子树的节点个数为n-1-lsz-rsz。贪心的&#xff0c;那么二号玩家其实可以占据…
阅读更多...
Java基础学习笔记（十八）—— 转换流、对象操作流

Java基础学习笔记（十八）—— 转换流、对象操作流

转换流、对象操作流1 转换流1.1 构造方法1.2 指定编码读写2 对象操作流2.1 对象操作流概述2.2 对象序列化流2.3 对象反序列化流2.4 案例1 转换流 1.1 构造方法 转换流就是来进行字节流和字符流之间转换的 InputStreamReader&#xff1a;是从字节流到字符流的桥梁&#xff0c;…
阅读更多...
Linux（八）线程概念

Linux（八）线程概念

1、线程的本质 线程就是一个进程内部的控制序列 是CPU进行执行调度的基本单元。&#xff08;调度一段代码的执行是通过线程完成的&#xff09; 一个进程中至少有一个线程&#xff08;所以进程与线程的数量关系是 一对一 或 一对多&#xff09; 2、为什么把线程称为LWP LWP…
阅读更多...
数学建模之熵权法（SPSSPRO与MATLAB）

数学建模之熵权法（SPSSPRO与MATLAB）

数学建模之熵权法&#xff08;SPSSPRO与MATLAB&#xff09;一、基本原理对于某项指标&#xff0c;可以用熵值来判断某个指标的离散程度&#xff0c;其信息熵值越小&#xff0c;指标的离散程度越大(表明指标值得变异程度越大&#xff0c;提供的信息量越多)&#xff0c;该指标对综…
阅读更多...
Maxout 激活函数与 Max-Feature-Map (MFM)

Maxout 激活函数与 Max-Feature-Map (MFM)

前言 最近在读 A Light CNN for Deep Face Representation With Noisy Labels 提到 maxout 激活函数&#xff0c;虽然很好理解&#xff0c;激活的时候选取最大值即可&#xff0c;但是具体细节看了看相关的资料反倒混淆了。参考了一个相关的视频&#xff0c;大致屡清楚为什么说…
阅读更多...
技术周 | qemu网络收发包流程

技术周 | qemu网络收发包流程

通常我们使用qemu创建虚拟机时&#xff0c;会使用下面的选项指定虚拟网卡设备的类型&#xff0c;以及桥接、tap设备参数等&#xff0c;如下&#xff1a; -device选项用于给虚拟机分配虚拟设备&#xff0c;如磁盘设备、网卡设备等 -netdev选项用于配置虚拟设备的后端&#xff0…
阅读更多...
MACD底背离选股公式以及技术指标公式

MACD底背离选股公式以及技术指标公式

今天介绍MACD底背离选股公式&#xff0c;整体来说编写难度比较大&#xff0c;按照MACD底背离的定义&#xff0c;需要分别找到2个价格波段低点以及快线DIF的2个低点&#xff0c;并进行比较&#xff0c;最终实现选股。 一、MACD底背离选股公式&#xff08;平替版&#xff09; 首先…
阅读更多...
ES6 简介（一）

ES6 简介（一）

文章目录ES6 简介&#xff08;一&#xff09;一、 概述1、 导读2、 Babel 转码器2.1 是什么2.2 配置文件 .babelrc2.3 命令行转码2.4 babel-node2.5 babel/register2.6 polyfill2.7 浏览器环境二、 变量1、 let2、 const3、 ES6 声明变量4、 顶层对象的属性5、 globalThis 对象…
阅读更多...
TCP协议面试灵魂12 问（二）

TCP协议面试灵魂12 问（二）

为什么不是两次&#xff1f; 根本原因: 无法确认客户端的接收能力。 分析如下: 如果是两次&#xff0c;你现在发了 SYN 报文想握手&#xff0c;但是这个包滞留在了当前的网络中迟迟没有到达&#xff0c;TCP 以为这是丢了包&#xff0c;于是重传&#xff0c;两次握手建立好了…
阅读更多...
机器视觉高速发展催热人工智能市场，深眸科技深度布局把握新机遇

机器视觉高速发展催热人工智能市场，深眸科技深度布局把握新机遇

曾经&#xff0c;冰箱侧身的标签、空调背面不显眼的小螺丝、微波炉角落里的型号编码等质量检测&#xff0c;是工业生产线中最费人工、最难检测的“老大难”。这主要是因为我国家电行业长期以混产为主要生产方式&#xff0c;一条生产线上可能有几十种型号的钣金件产品同时经受质…
阅读更多...
文档存储Elasticsearch系列--2 ES内部原理

文档存储Elasticsearch系列--2 ES内部原理

前言&#xff1a;ES作为nosql 的数据存储&#xff0c;为什么它在承载PB级别的数据的同时&#xff0c;又可以对外提高近实时的高效搜索&#xff0c;它又是通过什么算法完成对文档的相关性分析&#xff1b;又是怎么保证聚合的高效性&#xff1b; 1 ES 分布式文档存储&#xff1a…
阅读更多...
人工智能导论——谓词公式化为子句集详细步骤

人工智能导论——谓词公式化为子句集详细步骤

在谓词逻辑中&#xff0c;有下述定义&#xff1a; 原子&#xff08;atom&#xff09;谓词公式是一个不能再分解的命题。 原子谓词公式及其否定&#xff0c;统称为文字&#xff08;literal&#xff09;。PPP称为正文字&#xff0c;P\neg PP称为负文字。PPP与P\neg PP为互补文字。…
阅读更多...
MySQL实战作业示例：从离线文件生成数据库

MySQL实战作业示例：从离线文件生成数据库

前言 MySQL实战的课后作业&#xff0c;作业内容具体见 https://bbs.csdn.net/topics/611904749 截至时间是 2023年2月2日&#xff0c;按时提交的同学有一位。确实这次的作业非常有挑战性&#xff0c;作业用到的内容没有百分之百的学过&#xff0c;需要大家进行深入而有效的搜索…
阅读更多...
【MyBatis】高级映射多对一,一对多和延迟加载

【MyBatis】高级映射多对一,一对多和延迟加载

数据库准备:1. 多对一:多个学生对应一个班级(学生表是主表, 班级表是副表)多种实现方式, 常见的包括三种第一种方式&#xff1a; 一条sql语句, 级联属性映射// StudentMapper.xml // 一条sql语句, 级联属性映射 <resultMap id"studentResultMap" type"Studen…
阅读更多...
Java当中的AQS

Java当中的AQS

一、什么是AQS AQS的全称是:AbstractQueuedSynchronizer AQS是java当中的一个抽象类&#xff0c;用来构建锁和同步器。 例如我们常见的ReentrantLock&#xff0c;Semaphore等等都是通过AQS来构建的。 AQS的原理 如果被请求的共享资源没有被占用&#xff0c;那么就把请求资源…
阅读更多...
spring boot集成xxl job

spring boot集成xxl job

目录 1.xxl job介绍 2.搭建说明 (1)配置调度中心 (2)配置执行器 (3).执行 1.xxl job介绍 官网地址:分布式任务调度平台XXL-JOB XXL-JOB是一个分布式任务调度平台&#xff0c;其核心设计目标是开发迅速、学习简单、轻量级、易扩展。 2.搭建说明 环境搭建主要分为两个部分…
阅读更多...
《深入浅出计算机组成原理》学习笔记 Day19

《深入浅出计算机组成原理》学习笔记 Day19

冒险和预测&#xff08;三&#xff09;乱序执行参考乱序执行 尽管代码生成的指令是顺序的&#xff0c;但是如果后面的指令和前面的指令独立&#xff0c;完全不需要等待前面的指令运算完成&#xff0c;可以先执行。 这种解决方案称为乱序执行&#xff08;Out-of-Order Executi…
阅读更多...
程序加载与运行过程中的资源分配与管理

程序加载与运行过程中的资源分配与管理

目录 程序的加载 程序的内存空间 程序入口地址 BSS段初始化 程序运行过程中的堆栈管理 栈内存管理 变量的作用域&#xff1a; 栈溢出攻击原理 Linux堆内存管理 查看进程内存布局 内存分配器 内存块合并 top chunk 程序的运行分两种情况&#xff1a;一种是在有操作…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023