数学建模之熵权法（SPSSPRO与MATLAB）

一、基本原理

对于某项指标，可以用熵值来判断某个指标的离散程度，其信息熵值越小，指标的离散程度越大(表明指标值得变异程度越大，提供的信息量越多)，该指标对综合评价的影响（即权重）就越大，如果某项指标的值全部相等，则该指标在综合评价中不起作用。因此，可利用信息熵这个工具，计算出各个指标的权重，为多指标综合评价提供依据。

指标的值变化会直接影响因素的变化，变化量越大，说明指标对于因素的变化作用也应该是越明显的。

二、分析

1、适用范围:

可用于任何评价问题中的确定指标权重;
可用于剔除指标体系中对评价结果贡献不大的指标
注意:确定权重前需要确定指标对目标得分的影响方向，对非线性的指标要进行预处理或者剔除。

2、优点:

能深刻反映出指标的区分能力，进而确定权重
是―种客观赋权法，相对主观赋权具有较高的可信度和精确度算法简单

3、缺点:

不够智能，没有考虑指标与指标之间的影响，如:相关性、层级关系等若无业务经验指导，权重可能失真
对样本的依赖性较大，随着建模样本不断变化，权重会发生一定波动

4、关键点

研究：评价类问题
依据：利用信息熵计算各个指标的权重
目的：为多指标综合评价提供依据。

三、补充数学概念

1.正向指标：

指标值越大，则评价就越好。与此相对的是负向指标。
举例：场均得分----越大越好----正向指标，场均失误----越小越好----负向指标。

2.信息量

计算公式：I（x）=-ln(p(x))

公式推导：
<越有可能发生的事情包含的信息量越小>
将信息量用字母I表示，概率用p表示，那么我们可以将它们建立一个函数关系：

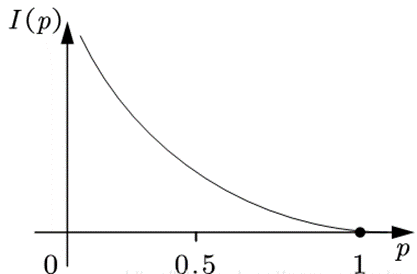
假设 x 表示事件 X 可能发生的某种情况，p(x)表示该事件发生的概率，那么I(p)=−ln(p(x)) ，因为 0⩽p(x)⩽1 ，所以I(x)⩾0 。
说明：此处的I(p)=−ln(p(x)),其中的对数是以e为下标的，也可将2作为下标，对此，目前没有统一要求。

3.信息熵

事件X的信息熵H(X)如下:

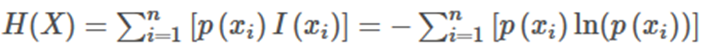
从公式可以看出，信息熵本质上就是对信息量的期望，且式中唯一的未知数是事件x的概率。

四、案例分析

编号	语文	数学	英语	总分
甲	90	10	60	160
乙	70	30	60	160
丙	10	90	60	160
订	80	20	60	160

这四个同学谁的综合成绩最好？

1、数据标准化

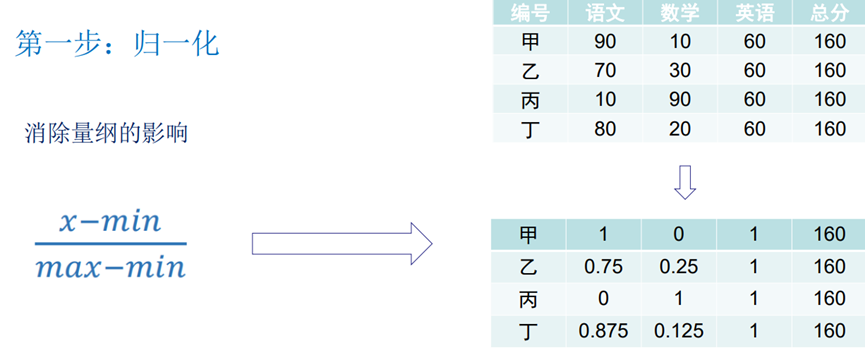
SPSSPRO操作：

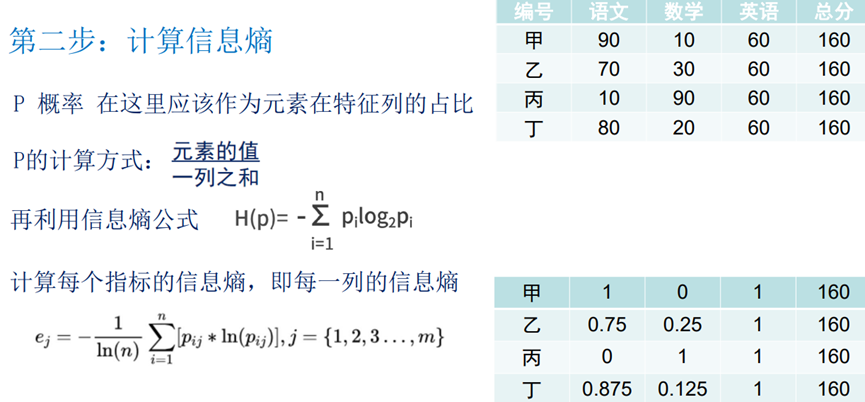
2、计算信息熵

熵权法
项	信息熵值e	信息效用值d	权重(%)
语文_min-max标准化	0.788	0.212	31.97
数学_min-max标准化	0.549	0.451	68.03

3、确定权重

综合得分表

行索引	综合评价	排名
1	0.31973321396603943	4
2	0.4098666069830197	2
3	0.6802667860339606	1
4	0.36479991047452953	3

4、Matlab代码：

disp('输入矩阵A');
A=input('A=');
%%D=max(A);
%%归一化%%
[n,m] = size(A);
minguiyi=repmat(min(A),n,1);
maxguiyi=repmat(max(A),n,1);
B=(A-minguiyi) ./ (maxguiyi-minguiyi);
% disp('归一化结果为 B=  ');
% disp(B);
%%计算信息熵%%
C=B./repmat(sum(B),n,1);
% disp(' P的矩阵为 P=  ');
% disp(C);%%C是概率矩阵
 
for i = 1:n
    for j =1:m
        ifC(i,j) == 0
           D(i,j)=0;
            
        else
           D(i,j) = C(i,j)*log(C(i,j));
        end
    end
end
E=-sum(D)/log(n);%%每一列的信息熵
 
%%计算每个指标的信息效用值%%
F=1-E;
%%权重的计算；
sq=F/sum(F,2);
 
%%加上权重比较%%
A_=sum(A.*repmat(sq,n,1),2);
disp('加权结果为:');
disp(A_);