- 层序遍历 10
- 226.翻转二叉树
- 101.对称二叉树 2
102.二叉树的层序遍历
力扣题目链接
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。

接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:

var levelOrder =function(root){
if(!root) return []
const queue = [root]
const res = []
while(queue.length){
//level用来存储每一层的节点值
const level = []
const len = queue.length
for(let i = 0; i < len; i++){
const node = queue.shift()
level.push(node.val)
//queue用来存储下一层的节点
if(node.left) queue.push(node.left)
if(node.right) queue.push(node.right)
}
res.push(level)
}
return res
}
//代码随想录答案
var levelOrder = function(root) {
//二叉树的层序遍历
let res = [], queue = [];
queue.push(root);
if(root === null) {
return res;
}
while(queue.length !== 0) {
// 记录当前层级节点数
let length = queue.length;
//存放每一层的节点
let curLevel = [];
for(let i = 0;i < length; i++) {
let node = queue.shift();
curLevel.push(node.val);
// 存放当前层下一层的节点
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
//把每一层的结果放到结果数组
res.push(curLevel);
}
return res;
};226.翻转二叉树
力扣题目链接(opens new window)
翻转一棵二叉树。

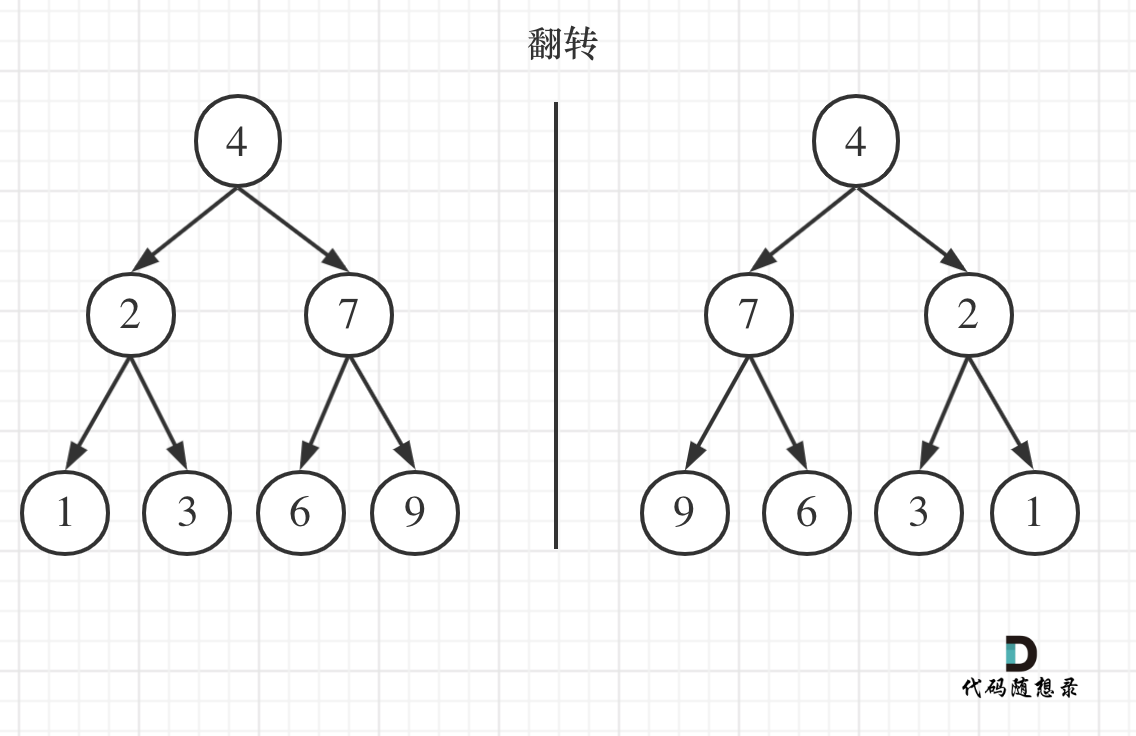
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
关键在于遍历顺序,前中后序应该选哪一种遍历顺序? (一些同学这道题都过了,但是不知道自己用的是什么顺序)
遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。
注意只要把每一个节点的左右孩子翻转一下,就可以达到整体翻转的效果
这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便,因为中序遍历会把某些节点的左右孩子翻转了两次!建议拿纸画一画,就理解了
那么层序遍历可以不可以呢?依然可以的!只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的!
递归法

var invertTree = function(root) {
if(!root) return null
const queue = [root]
while(queue.length){
const node = queue.shift()
const temp = node.left
node.left = node.right
node.right = temp
if(node.left) queue.push(node.left)
if(node.right) queue.push(node.right)
}
return root
}
//代码随想录的答案
//使用递归版本的前序遍历
var invertTree = function(root) {
// 终止条件
if (!root) {
return null;
}
// 交换左右节点
const rightNode = root.right;
root.right = invertTree(root.left);
root.left = invertTree(rightNode);
return root;
};
// 使用迭代版本(统一模板))的前序遍历:
var invertTree = function(root) {
//我们先定义节点交换函数
const invertNode = function(root, left, right) {
let temp = left;
left = right;
right = temp;
root.left = left;
root.right = right;
}
//使用迭代方法的前序遍历
let stack = [];
if(root === null) {
return root;
}
stack.push(root);
while(stack.length) {
let node = stack.pop();
if(node !== null) {
//前序遍历顺序中左右 入栈顺序是前序遍历的倒序右左中
node.right && stack.push(node.right);
node.left && stack.push(node.left);
stack.push(node);
stack.push(null);
} else {
node = stack.pop();
//节点处理逻辑
invertNode(node, node.left, node.right);
}
}
return root;
};
// 使用层序遍历:
var invertTree = function(root) {
//我们先定义节点交换函数
const invertNode = function(root, left, right) {
let temp = left;
left = right;
right = temp;
root.left = left;
root.right = right;
}
//使用层序遍历
let queue = [];
if(root === null) {
return root;
}
queue.push(root);
while(queue.length) {
let length = queue.length;
while(length--) {
let node = queue.shift();
//节点处理逻辑
invertNode(node, node.left, node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return root;
};
101. 对称二叉树
力扣题目链接(opens new window)
给定一个二叉树,检查它是否是镜像对称的。


var isSymmetric = function(root) {
if(root === null) {
return true;
}
let stack = [];
stack.push(root.left);
stack.push(root.right);
while(stack.length) {
let right = stack.pop();
let left = stack.pop();
if(left === null && right === null) {
continue;
}
if(left === null || right === null) {
return false;
}
if(left.val !== right.val) {
return false;
}
stack.push(left.left);
stack.push(right.right);
stack.push(left.right);
stack.push(right.left);
}
return true;
}
// @lc code=end
var root = {
val: 1,
left: {
val: 2,
left: {
val: 3,
left: null,
right: null
},
right: {
val: 4,
left: null,
right: null
}
},
right: {
val: 2,
left: {
val: 4,
left: null,
right: null
},
right: {
val: 3,
left: null,
right: null
}
}
}
console.log(isSymmetric(root));
//代码随想录的方法
// 递归判断是否为对称二叉树:
var isSymmetric = function(root) {
// 使用递归遍历左右子树 递归三部曲
// 1. 确定递归的参数 root.left root.right和返回值true false
const compareNode = function(left, right) {
// 2. 确定终止条件 空的情况
if(left === null && right !== null || left !== null && right === null) {
return false;
} else if(left === null && right === null) {
return true;
} else if(left.val !== right.val) {
return false;
}
// 3. 确定单层递归逻辑
let outSide = compareNode(left.left, right.right);
let inSide = compareNode(left.right, right.left);
return outSide && inSide;
}
if(root === null) {
return true;
}
return compareNode(root.left, root.right);
};
// 队列实现迭代判断是否为对称二叉树:
var isSymmetric = function(root) {
// 迭代方法判断是否是对称二叉树
// 首先判断root是否为空
if(root === null) {
return true;
}
let queue = [];
queue.push(root.left);
queue.push(root.right);
while(queue.length) {
let leftNode = queue.shift(); //左节点
let rightNode = queue.shift(); //右节点
if(leftNode === null && rightNode === null) {
continue;
}
if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
return false;
}
queue.push(leftNode.left); //左节点左孩子入队
queue.push(rightNode.right); //右节点右孩子入队
queue.push(leftNode.right); //左节点右孩子入队
queue.push(rightNode.left); //右节点左孩子入队
}
return true;
};
// 栈实现迭代判断是否为对称二叉树:
var isSymmetric = function(root) {
// 迭代方法判断是否是对称二叉树
// 首先判断root是否为空
if(root === null) {
return true;
}
let stack = [];
stack.push(root.left);
stack.push(root.right);
while(stack.length) {
let rightNode = stack.pop(); //左节点
let leftNode=stack.pop(); //右节点
if(leftNode === null && rightNode === null) {
continue;
}
if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
return false;
}
stack.push(leftNode.left); //左节点左孩子入队
stack.push(rightNode.right); //右节点右孩子入队
stack.push(leftNode.right); //左节点右孩子入队
stack.push(rightNode.left); //右节点左孩子入队
}
return true;
};