2024华为OD机试(C卷+D卷)最新题库【超值优惠】Java/Python/C++合集

题目描述
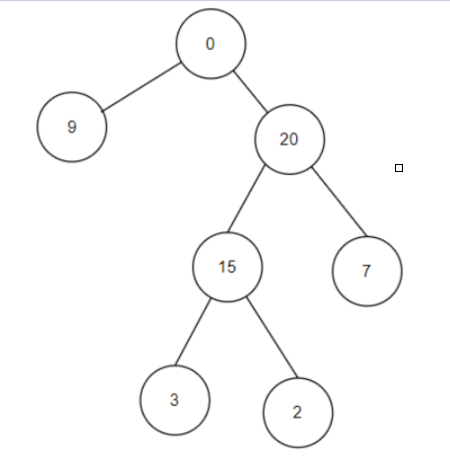
给定一个二叉树,每个节点上站一个人,节点数字表示父节点到该节点传递悄悄话需要花费的时间。
初始时,根节点所在位置的人有一个悄悄话想要传递给其他人,求二叉树所有节点上的人都接收到悄悄话花费的时间。
输入描述
给定二叉树
0 9 20 -1 -1 15 7 -1 -1 -1 -1 3 2
注: -1 表示空节点
输出描述
返回所有节点都接收到悄悄话花费的时间
38
示例1
输入:
0 9 20 -1 -1 15 15 7 -1 -1 -1 -1 3 2
输出:
38
题解
题目分析
这道题属于树的深度优先搜索(DFS)算法题目。我们需要在给定的二叉树中找到从根节点开始将悄悄话传递到所有节点所需的最大时间。题目的关键在于如何通过递归遍历树的每个节点,并记录下传递悄悄话所需的时间。
解题思路
- 构建树的表示:给定的是二叉树的层序遍历列表,其中
-1表示空节点。我们需要将其转换为树结构。- 深度优先搜索(DFS):使用DFS遍历树,计算从根节点传递悄悄话到叶子节点的最大时间。
- 递归计算:对于每个节点,递归计算其左子树和右子树的传递时间,取两者中的较大值,再加上当前节点的时间值即为该节点的总时间。
Python
arr = list(map(int, input().split()))
n = len(arr)
def dfs(idx):
"""
使用深度优先搜索算法计算从根节点开始传递悄悄话到叶子节点的最大时间。
参数:
idx (int): 当前节点在数组中的索引。
返回:
int: 从当前节点到叶子节点的最大时间。
"""
global n
max_cost_time = 0
# 计算当前节点的左右子节点的索引
left_idx, right_idx = 2 * idx + 1, 2 * idx + 2
# 递归计算左子树的最大时间
if left_idx < n and arr[left_idx] != -1:
max_cost_time = max(max_cost_time, dfs(left_idx))
# 递归计算右子树的最大时间
if right_idx < n and arr[right_idx] != -1:
max_cost_time = max(max_cost_time, dfs(right_idx))
# 返回当前节点的时间加上其子树的最大时间
return arr[idx] + max_cost_time
# 从根节点开始计算
print(dfs(0))
🙏整理题解不易, 如果有帮助到您,请给点个赞 ❤️ 和收藏 ⭐,让更多的人看到。🙏🙏🙏