这个专栏主要是用来分享一下我在 机器学习中的 学习笔记及一些感悟，也希望对你的学习有帮助哦！感兴趣的小伙伴欢迎 私信或者评论区留言！这一篇就更新一下《 白话机器学习中的数学——线性不可分》！

目录

一、什么是线性不可分

二、算法分析

三、总结

---

一、什么是线性不可分

线性不可分简单来说就是你一个数据集不可以通过一个线性分类器（直线、平面）来实现分类。这样子的数据集在实际应用中是很常见的，例如：人脸图像、文本文档等。

二、算法分析

线性不可分就是用直线不能分类的问题，比如下面这个图片：

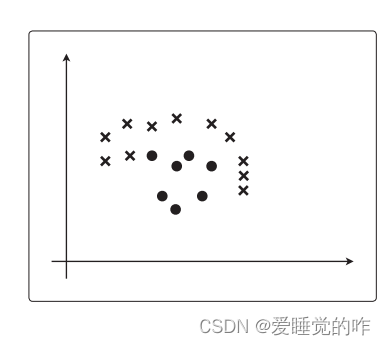
 对于这个例子来说，虽然用直线不能分类，但是用曲线是 不是就可以分类了：

所以我们要像学习多项式回归时那样，去增加次数，我们就向训练数据中加入，考虑这样的数据：

也就是：

 

假设 θ 是这样的向量，那么 θTx ⩾ 0 的图形是什么样的呢？

 

因为 θTx ⩾ 0，先代入看看吧，然后像之前一样，变形试试 ：

移项后最终得到的表达式是  ⩾ 。将这个画成图看看： 

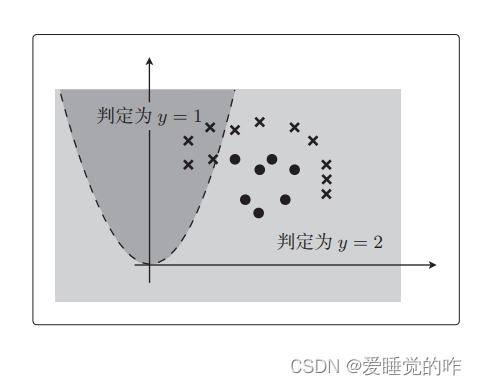
三、总结

之前的决策边界是直线，现在则是曲线了。参数 θ 是随便 定的，所以数据完全没有被正确地分类。不过，我们知道将逻辑回归应用于线性不可分问题的方法了。并不是很难。

之后通过随意地增加次数，就可以得到复杂形状的决策边界了。 比如在 之外再增加一个 ，就会有圆形的决策边界。在逻辑回归的参数更新中也可以使用随机梯度下降法。

逻辑回归虽然有点难，但是我们最后也求出它的参数更新表达式了。还有一个名为 SVM，也就是支持向量机的分类算法也很有名。此 外，还有多分类的做法，去学一学也是很有意思的

好啦！今天的分享就到这里啦！感兴趣的小伙伴欢迎评论区交流或者私信博主哦！