---

最近公共祖先

题目链接

思路：

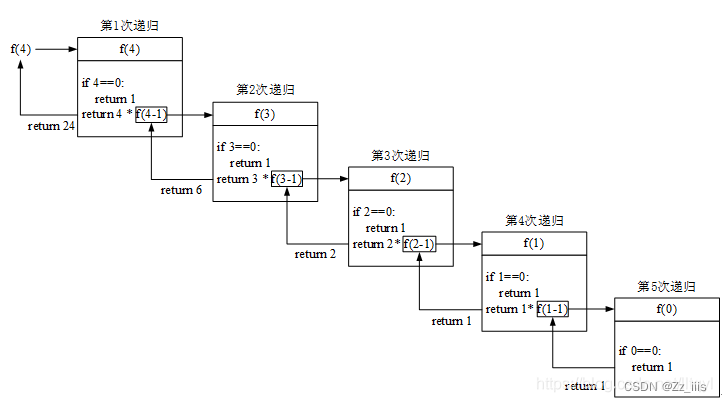
题目所描述的满二叉树如下：

上述树中子节点与父节点之间的关系为root = child / 2
所以如果a ！= b，就让其中的较大数除以2， 如此循环直到a == b 即是原来两个数的最近公共祖先。
比如： 求2和7的最近公共祖先：

• 2和7不相等，2不动，用较大的数7除2算出7的根为3
• 2和3比还是不相等，2不动，3再除2算出3的根是1
• 接下来1和2比，2大了，1不动，用较大的2除2算出2的根是1
• 1和1比相等了，循环停止，此时相等的值就是公共祖先。

代码：

//非递归版本
class LCA {
public:
    int getLCA(int a, int b) {
        while (a != b)
        {
            if (a > b)
                a /= 2;
            else
                b /= 2;
        }
        return a;
    }
};
//递归版本
class LCA {
  public:
    int getLCA(int a, int b) {
        // write code here
        if (a == b)
            return a;

        if (a > b) {
            a = a / 2;
        } else {
            b = b / 2;
        }

        return getLCA(a, b);
    }
};

---

求最大连续bit数

题目链接

思路：

最佳思路：
让1每次左移一位，然后和输入的值做与运算，获取其每一位的二进制值。获取第i位的值： n &( 1<< i )。如果1连续，则计数累加，如果不连续，则count从0开始计数。根据题意，
如果是byte类型的数据，利用for循环，把1从0开始，左移7位之后结束统计
如果是int类型的数据，利用for循环，把1从0开始，左移32位之后结束统计
好处：适用于正数、0和负数。

代码：

#include<iostream>
using namespace std;
int main() {
    int a = 0;
    cin >> a;
    int max_count = 0;
    int count = 0;
    //通法 适用于正数和负数
    for(int i=0;i<32;i++)
    {
        if(a&(1<<i))
        {
            count++;
            max_count = max(max_count,count);//每加一次就更新一下
        }
        else 
        {
            count=0;
        }
    }

    cout << max_count;
    return 0;
}

---

end