原文来自微信公众号“编程语言Lab”: 学习驱动的复杂软件符号执行
搜索关注“编程语言Lab”公众号(HW-PLLab)获取编程语言更多技术内容!
欢迎加入编程语言社区 SIG-编程语言测试,了解更多 编程语言测试相关的技术内容。
加入方式:添加文末小助手微信,备注“加入 SIG-编程语言测试”。
作者简介
卜磊,南京大学计算机科学与技术系教授,博士生导师。研究领域是软件工程与形式化方法,包括模型检验技术,实时混成系统,信息物理融合系统等。
个人主页:https://cs.nju.edu.cn/bulei/
视频回顾
SIG-编程语言测试技术沙龙回顾|学习驱动的复杂软件符号执行
研究背景
软件深入我们生活的方方面面,在软件定义一切的时代,软件的正确运行是非常重要的。软件测试是保障软件正确运行的一种有效手段。而测试用例生成是影响软件测试效率的关键因素。那么,我们应该怎样去做测试用例生成呢?

测试用例自动生成技术基本分为以下两类:
随机测试技术
包括适应性随机测试,模糊测试等等。给定一段代码,我们“随机乱来”,“大力出奇迹”,看测试结果如何。这种方式生成的测试用例基本上有两个特点,一是覆盖度较低,这是因为很多用例都走了相同的主干流程,程序中的 Corner Case 没有被执行到;此外,会有大量的冗余测试用例。
基于符号执行的测试技术
基于符号执行的测试技术,当前学术界经常在提,但还未在工业界完全落地。符号执行的基本概念是,我不知道哪个具体输入可以往下执行,但是我知道代码里面有这样一条路径还没有走到,那么我们会尝试将这条路径中的约束符号化抽取出来,通过对约束进行求解,从而生成能执行这条路径的具体用例。
鉴于每个路径生成出来的用例都不一样,所以相对来讲,这种方式自动化程度较高,覆盖度也很高,也解决了用例冗余的问题。
符号执行
符号执行具体怎么做呢,它会使用符号化的变量去代替一个具体的输入去执行程序。与随机测试生成不同的是,符号执行不会给变量一个具体的值,而是让变量带着约束往下执行(比如,随机测试会给定  ,然后往下走,而符号化是
,然后往下走,而符号化是 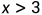 往左走,
往左走, 往右走之类)。
往右走之类)。
符号执行会时刻维护每个分支路径下的路径约束,然后调用求解器对路径约束求解以生成测试用例。

代表工具
包括大名鼎鼎的 KLEE(面向 C 代码),SPF(面向 Java 代码),Pex(后续集成到了 Visual Studio)等,都是比较有代表性的符号执行的工具。
KLEE:https://klee.github.io/
SPF:https://github.com/SymbolicPathFinder/jpf-symbc
Pex:https://www.microsoft.com/en-us/research/publication/pex-white-box-test-generation-for-net/
示例
我们看如下示例。初始时 result = 0,如果满足 x > y 那么 result = x - y,否则执行 y - x,这是两个简单的分支。然后再执行一个 assert(result > 0)。
static void example(int x, int y) {
int result = 0;
if (x> y)
result = x - y;
else
result = y - x;
assert(result> 0);
}假设我们对上述示例代码做测试,符号执行是将对应的 CFG(控制流图)画出来(如下图示),自动地生成代码中的约束。基于 CFG 分析,要使得测试用例一定走到某个路径分支下,我们的约束应该维持什么样的形式。

比如,要走到最左边这个分支,路径需要满足约束是:

当我们有了对应约束后,可以丢给 SMT 等求解器去求解。解出来的就是一个可走该路径的测试用例。解不出来,则表示这条路径不可达。

然而,当我们将符号执行应用到真实的大系统中时,会面临几个主要的挑战:
挑战 1:复杂数值计算
传统的符号执行会先收集完所有的路径约束后,再去做求解,因此非常依赖于底层求解器的能力。我们来看下面的示例,double a = x - y * 2,double b = x * y / (x + y),double c = sin(x) + cos(sqrt(y)) 都是在数值计算中十分常见的,尤其像我们组一直合作的航天、列控等领域中存在大量的类似代码,比如会有角速度等计算,用现有的 SMT 去求解是不可能的。在这种情况下,传统的符号执行基本上会无法求解。
static void example(double x, double y) {
double a = x - y * 2;
double b = x * y / (x + y);
double c = sin(x) + cos(sqrt(y));
if(a > y) assert(false);
if(b < x) assert(false);
if(c > 0) assert(false);
}挑战 2:黑和函数调用
符号执行另外一个挑战就是函数的调用使得我们难以获取函数内部的实现细节,特别是大规模的系统中,背后一定会调用很多库函数或者第三方的包。比如说下面这段代码,有一个函数调用 Long.numberOfLeadingZeros(x),传了 x 做参数。这时,我们需要生成一个测试用例,可以保证走下去这个函数调用,这对符号执行是不可能的事情。如果这个函数的实现我们不知道,这种情况下要对其白盒化符号执行是无法完成的。
static void example(long x, double y) {
double z = Long.numberOfLeadingZeros(x);
if(z> x) assert(false);
}相关工作
接下来简单介绍一下业界有关解决上述挑战问题的相关工作。
基于 SMT 约束求解器的符号执行工具
代表工作是 Pex [1],底层基于 Z3 [2] 实现,可以处理线性的约束,但对非线性约束支持有限。
基于简化的约束求解技术的符号执行工具
代表工作有 jCUTE [3],SPF-Mixed [4] 等,这些工具可以简化约束做抽象,但降低了复杂约束求解的可能性,效果也不是特别好。
基于搜索的约束求解技术的符号执行工具
代表工作有 CORAL [5],Concolic Walk [6]。这类工具是基于启发式搜索来做符号执行,通过猜测一些可能的值往下走。但是这类工具对参数比较敏感,同时背后的逻辑是基于一些遗传算法来做猜测,无法保证覆盖率,缺乏理论保证。
基于机器学习的复杂约束优化方法
我本身的研究其实偏形式化、程序分析和验证。机缘巧合的是,当时我们在做相关的复杂系统,包括列控的一些工作时,与南大的同事,人工智能学院俞扬教授,交流非线性的约束无法处理,俞教授推荐了他们的工作,AI 领域的基于分类学习的无梯度优化技术。虽然和我们遇到的情况不完全一致,但多少有一些相关,因此我们就去了解了一下。
无梯度优化面对的优化问题本身可能只是一个函数表示(比如做运筹或优化 / 最小化)。但优化问题 F 内部实现是什么,对我们来说可能是黑盒。
那么这个基于学习分类的无梯度优化怎么做的呢,给定一个优化模型 M(即取值区间),一个优化问题 F,通过对可能的取值 X 采样,在 F 中去确认和评估,再对返回的评估值进行学习与收敛。

因此,这背后的逻辑,就是机器学习的思路,基于大量样例进行统计:拿着大量的采样点给优化问题试,试了后好不好给我反馈,反馈后我们去收敛迭代,朝着好的方向努力,然后将找到的最好的值输出。
对于我而言,我感兴趣的是,在这种情况下非线性的约束是可以被处理的(因为在这个框架下,目标优化问题 F 本身可以是黑盒,只要能对评估点做确认即可,所以不管 F 是否是线性的,都能够去尝试优化)。
我们举一个简单的示例来说明下俞教授提出的这个基于分类学习的无梯度优化是怎么运行的。假设如下是我们的一个优化问题 F:
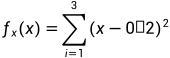
图中学习模型指的是  、
、 、
、 的取值范围。然后,我们可以“眼睛闭起来猜”。比如,第一轮
的取值范围。然后,我们可以“眼睛闭起来猜”。比如,第一轮  、
、 、
、 我们猜测是 1.5、2.4、5.1,第二轮是 2.6、-1.4、2.0……我们将猜测的值放回 F 去做评估。F 会将求出的值反馈出来,比如前面的第一轮值反馈是 24,第二轮是 11.56……那么,这样的一系列值会反馈给学习模型,并且可以根据返回值的大小去做排序,并去划分正负样本。一旦有了正负样本,底层的学习模块就可以逐步对采样的取值区间做收敛,尝试逼近目标函数的最优解。
我们猜测是 1.5、2.4、5.1,第二轮是 2.6、-1.4、2.0……我们将猜测的值放回 F 去做评估。F 会将求出的值反馈出来,比如前面的第一轮值反馈是 24,第二轮是 11.56……那么,这样的一系列值会反馈给学习模型,并且可以根据返回值的大小去做排序,并去划分正负样本。一旦有了正负样本,底层的学习模块就可以逐步对采样的取值区间做收敛,尝试逼近目标函数的最优解。

这让我产生了结合的想法,我们能否将以上的思路应用在复杂代码的测试用例生成当中呢?
基于机器学习约束求解的符号执行框架
鉴于上述无梯度优化方法要用起来得要给它一个优化问题,并且要能够给出反馈,而这个问题本身的形式并不重要,只要能对采样值进行确认和反馈就行,那么对我而言,我需要将约束的可满足性问题转化为一个优化问题。此外,与之前的框架不同的是,若要将机器学习作为底层的约束求解器,实际上要求符号执行框架是迭代式的,这就是我们需要做的另一件事情。
Question 1: 如何将约束的 满足性问题 转化为 优化问题 ?
我们先来看第一个问题。即将路径的可满足性问题转化成一个优化问题。对于约束而言,要有一个最优解,因此我们定义了一个不满足程度函数:
度量一组采样对约束的不满足程度
将约束的 满足性问题 转化为 不满足程度函数最小化的优化问题

当给定一组采样点后,我们只需要将约束放进去,计算一下约束的左值和右值,以及之间的 operator 关系是否成立。假设给定一个采样点 x = 3,y=5,约束是 ,成立,那么就可以说这组采样值对于这个约束而言不满足度是 0。如果猜的采样点是 x=5,y=3,那么这个采样点对于此约束不成立,离成立有多远呢?我们的方法很简单,左值减去右值取绝对值,即 。因此这个采样点对于该约束而言不满足度是 2。对于这一组路径上的所有约束而言,其整体的不满足度,就是将每一个子式的不满足度加起来。
以上的方式,在当我们给定一组采样点后,可以将整个路径约束的可满足性问题变成一个优化问题。如果猜的这组采样值,可以使得所有的约束全部满足,那么整体的不满足度是 0,只要有一个是不满足的,整体的不满足度一定是个正值。因此,对于机器学习求解器而言,它可以不需要知道具体实现,直接往最小值/最优解去逼近。如果它能得到 0,表示它猜出来一个使得整体约束完全满足的点,也就是一个测试用例。如果它最后获得的值还是正值,那就表明这条路径还是没有解出来,这种情况下,即使让程序员去覆盖这条路径,也是很难的。
我们举一个简单的例子来说明。
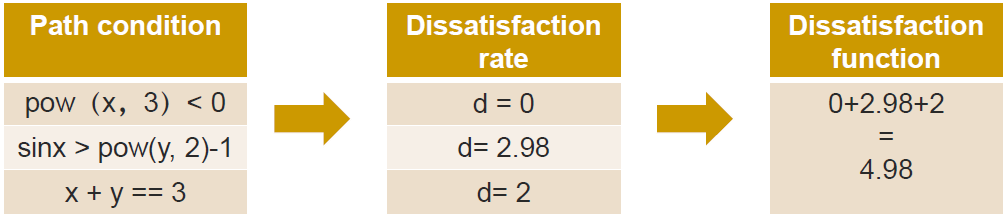
如上示例中,我们的路径约束有三个: ,
, ,
, ,假设采样点是
,假设采样点是 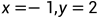 。带入每个约束:
。带入每个约束:
 成立,该约束的不满足度是 0
成立,该约束的不满足度是 0
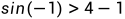 不成立,该约束的不满足度是
不成立,该约束的不满足度是 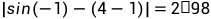
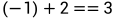 ,不成立,不满足度是
,不成立,不满足度是 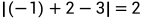
这一组约束的整体不满足度是 4.98。如果我们可以找到一组采样点,使得这三个约束同时满足,即整体不满足度为 0,那么我们的测试用例找到了。
Question 2: 如何设计一个 迭代式 的符号执行框架?
在前面的基础之上,我们进一步地做了如下工作,将符号执行引擎由拿到一个路径约束就去等约束求解器进行求解,改成拿到路径约束之后生成一个不满足度函数,用于学习模块不停地进行采样、评估和反馈,直到我们将反馈结果逼近到一个最优点,也就是 0 的形式。这需要符号执行引擎能够驱动代码在给定用例下迭代地执行并且反馈。因此,我们将框架进行了如下简单的修改,以满足上述要求。
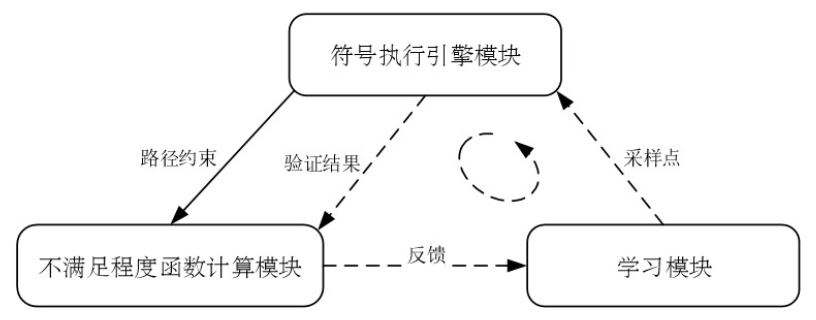
Question 3: 在基于机器学习的约束求解方法下如何 编码复杂路径约束 ?
接下来,我们面临的问题是如何处理复杂的路径约束。首先,针对如下的正常数值计算约束,可以用之前我们说的方法正常去处理。
线性路径约束:

非线性路径约束:
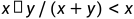
数学函数路径约束:

static void example(double x, double y) {
double a = x - y * 2;
double b = x * y / (x + y);
double c = sin(x) + cos(sqrt(y));
if(a > y) assert(false);
if(b < x) assert(false);
if(c > 0) assert(false);
}定义域路径约束
定义域问题
但是,因为我们的框架现在变成迭代式的,我们会额外遇到定义域带来的问题。举例来说,当给定一个约束后,在常规的符号执行情况下,我们直接丢给约束求解去解这个约束,解出来就往下走,解不出来那也没办法。而现在的情况是,给定一个采样点,我们会驱动代码去尝试这个采样点,看它对不对。如果我们猜的采样点,恰好是 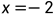 ,
, ,那么我们会得到
,那么我们会得到  ,这就违背了 log 函数的定义域限制。
,这就违背了 log 函数的定义域限制。

下面这个约束中,如果采样值  ,带入去确认的话,我们会得到除零错,甚至有可能为了尝试这个采样点,把整个程序搞崩掉。
,带入去确认的话,我们会得到除零错,甚至有可能为了尝试这个采样点,把整个程序搞崩掉。
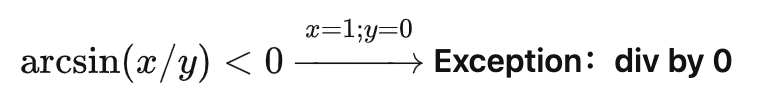
定义域路径约束生成规则
在测试的过程中,我们当然不希望为了用一个求解器去把原来的系统搞崩掉,但是如前面所描述,因为我们要不停地去确认,这是完全可能发生的。因此我们需要再加一个规则,即为每个约束分别定义一组(所谓的)定义域相关的路径约束生成规则。举例来说,第一个约束中因为 y 在分母上,我们需要补充  的规则,从而避免分母是 0 的情况。
的规则,从而避免分母是 0 的情况。

当我们拿到采样点后,我们需要先对采样点基于规则做一次过滤,如果满足过滤规则,则驱动它执行,否则直接返回它的不满足度。这是一个简单的度量规则。
黑盒函数路径约束
在定义域路径约束生成规则的基础上,我们可以进一步地去看如何处理黑盒函数了。这也是我认为该工作最有价值的部分。对于黑盒函数而言,由于我们采用的无梯度优化技术根本无需关心具体的目标函数的实现,所以黑盒函数的存在对于我们的方法没有影响,只要能驱动程序执行就可以。因此,我们可以直接调用库函数,将库函数的名字当做 operator,参数当做 operand。约束具体是什么并不重要,我们只需要给一个值让它跑起来,根据反馈迭代式地去逼近最优值即可。
每个库函数调用被封装为一个黑盒约束
库函数名字作为黑盒约束的操作符
库函数参数作为黑盒约束的操作数
回到之前的例子,我们无需知道 Long.numberOfLeadingZeros() 具体实现,假设给定一个采样点 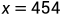 ,对于测试工程师来说,只要该函数能跑起来,我们将值带入函数调用,看反馈的结果是多少,是否满足约束
,对于测试工程师来说,只要该函数能跑起来,我们将值带入函数调用,看反馈的结果是多少,是否满足约束 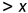 即可。假设该函数返回值是 55,那么其不满足度就是
即可。假设该函数返回值是 55,那么其不满足度就是  。当我们有了反馈后,就可以进一步去做逼近了。
。当我们有了反馈后,就可以进一步去做逼近了。

通过上述方式,我们可以尝试对大规模代码的函数调用进行处理了。
基于 MLBSE 的符号执行功能增强
MLBSE 框架简介
基于上述思路,我们给出了一个整体框架 MLBSE (Machine Learning Based Symbolic Execution) [7],如下图所示:
程序输入后:
传统符号执行的核心步骤,包括路径搜索策略、符号化变量、路径约束维护、符号化执行等全部复用经典符号执行的机制
在基本路径约束给定后,补充定义域约束、库函数的路径约束等
汇总约束后,采用反馈学习的形式去尝试得到最优值
在这个框架之上,我们进一步针对一些特定场景进一步做了功能增强。
针对包含函数调用的真实程序
我们以下面这个例子来说明。
static int max(int x, int y) {
if(x > y)
return x;
else
return y;
}
static book f(int x, int y){
int a = max(x, y);
assert(a > x + y);
}在常规白盒符号执行下,若存在函数调用,符号执行是将被调用函数的 CFG 内联到整个 CFG 中,然后将里面所有的部分都符号化执行,如下图所示。

白盒模式下的符号执行树
如果,我们只关心当前程序员写的这段代码,不关心调用函数的实现(比如库函数),那么我们无需对这样的函数实现进行测试。因此,如前面所述,我们可以直接用前面所提的黑盒方式来做符号执行。即,我们无需展开调用函数的 CFG,将其黑盒化,此时我们要遍历的路径/要求解的约束就少了很多,如下图所示。

黑盒模式下的符号执行树
针对路径约束求解失败的情况
此外,在传统的符号执行下,当你将约束丢给一个 SMT 去求解,SMT 会给出两种情况,满足时为 Ture,不满足时返回 False。满足就继续往下探索,不满足就直接回溯。

传统符号执行框架
而 MLBSE 是基于机器学习的,当没有找到最优解时,返回 False,不代表不可解,有可能只是在给定资源下没找到而已。这时直接回溯的话,可能会有很多路径就不会被探索了,那这时该怎么办呢?
我们利用了无梯度优化过程中另一个输出:可解置信度报告 ECS,供用户参考是否值得投入更多计算资源求解该路径约束。

MLBSE
符号执行路径搜索策略
在基于分类的无梯度优化框架下,给定搜索区间后,迭代中采用了哪些点,这些点的分布是怎样的,搜索区间之外还有多少区间是没有覆盖到的,这些是经常被问到的问题。我们对“还有多大的空间没有被覆盖”采用 ECS 值进行估值。实际上这个值的计算比较简单 [7],其数值也不具备绝对意义,但是,它有一定的参考意义。随着更多采样点的投入,其外部未探索的值会随之下降。因此,这个值可以提供一定参考,帮助我们判断是否有必要给更多的计算资源去求解该路径约束。

传统的符号执行搜索策略
基于可解置信报告 ECS,我们对路径搜索策略进行了扩展,首先定义一个可解置信度阈值 p,当给定一个路径约束后,若求解为 True,表明该路径可解;若为 False,则表明当前的区间内,路径约束求解失败,返回区间外未搜索的空间评估值(也就是 ECS)q,并与最初设定的阈值 p 进行比较,若高于最初设定的阈值,则表明外部残留的搜索空间还蛮大的,可以继续进行尝试,再拯救一下。

基于可解置信报告的搜索策略
比如,给定 3000 个样本数,没有成功求解出来,那么针对该条路径,我们可以将样本数翻倍,重新输入给求解器求解,直到区间外未搜索的空间估值 q 低于预期的阈值 p,那么表示底层求解器已经尽力了,我们就可以回溯了。
基于这套工作机制,我们优化了符号执行框架。虽然 ECS 无法给出一个准确的可信度量,但它对我们是否需要生成新用例给出了一定的参考和指导。因此,我们将 MLBSE 进行了进一步地优化,如下图所示:

基于机器学习约束求解的符号执行框架
工具实现与对比实验
整体实现
我们在 SPF 的基础上实现了一个基于机器学习的符号执行工具 —— MLB,以 SPF 为符号执行的核心,俞扬教授团队实现的 RACOS [8] 作为我们的无梯度优化引擎,进一步引入 jpf-nhandler 去处理库函数调用,同时利用 JaCoCo 生成测试用例的分析结果报告。

用户友好
该工具对用户友好,与现有的工具(要在里面写一堆的 annotation )相比,用户无需修改任何代码;其次,配置十分简单,在原来的 SPF 配置文件中新增被测目标(target,classpath)、采用的符号执行引擎(symbolic.dp)、以及采样点总数(symbolic.mlpm)即可。

配置文件

运行截图
可视化覆盖度报告
该工具可以生成相关的路径约束,并将求解结果以及相关的自动生成测试用例输入给 JaCoCo,输出可视化的测试用例覆盖度报告。


测试用例覆盖度报告
对比实验
简单介绍一下我们框架的实验和结果。
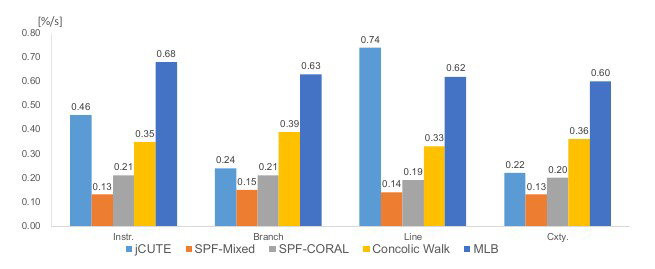
因为 MLB 是面向 Java 代码的,我们选用了 19 个 Java 程序做 benchmark,这些程序中包含一些复杂的数值计算和函数调用。对比工具包括经典的混合测试生成工具 jCUTE、SPF-Mixed,基于搜索的求解工具 SPF-CORAL 和 Concolic-Walk 等。被测程序基本上都会覆盖到三角函数、多项式计算、幂函数、方差等传统符号执行无法解决的问题。

覆盖度对比
MLB 生成的测试用例能更好地覆盖真实程序。

覆盖效率对比
相比其他工具,MLB 在测试用例生成的效率上更高。
采样点总数影响
在采样点数量较小时,覆盖度提升明显;当采样点数量较大时,覆盖度影响较小。

黑盒模式实验
Step 1:使用 The Apache Commons Math 提供的库函数改写 coral 求解器里的 Math 库函数
Step 2:MLB 和 Concolic Walk(基于启发式搜索的算法)分别使用黑盒模式和白盒模式为 coral 生成测试用例
结果表明,MLB 在白盒和黑盒模式上都比 Concolic Walk 表现更好;且 MLB 的黑盒模式比白盒模式下测试用例覆盖度更高,效率也更好。

可解置信度报告分析
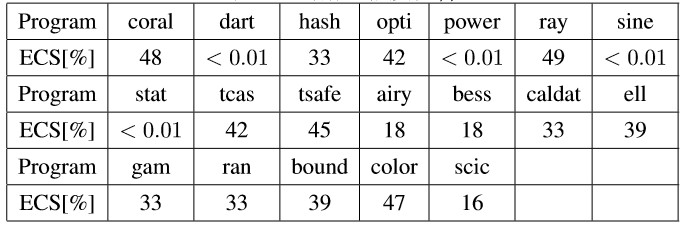
前面我们提到 MLB 可以生成 ECS,供用户参考是否需要投入更多的计算资源。我们分析前述实验生成的报告后发现,很多情况下 ECS 都小于 0.01%,这表示底层求解器认为仅有非常小的空间,它没有去针对采样尝试过。当然,也有一些场景下,ECS 达到了 30% 甚至 48%。
那 ECS 是否有它的真实意义呢?
我们进一步做了一件事情,即将每个周期采用的样本数 ×10,×100(即从 3000 变到 3 万再变到 30 万)。以 ECS 为 48% 的 coral 程序为例,实验结果表示,提高样本数量后,覆盖率的确有提高,且 ECS 的确有下降。而 ECS 小于 0.01% 时(以 dart 程序为例),样本数的增加并没有对 ECS 进行明显的影响。这表明,虽然 ECS 不能作为度量,但是它具有一定参考意义,可解置信度报告 ECS 可以让我们更合理地判断是否投入更多计算资源。

搜索策略对比实验
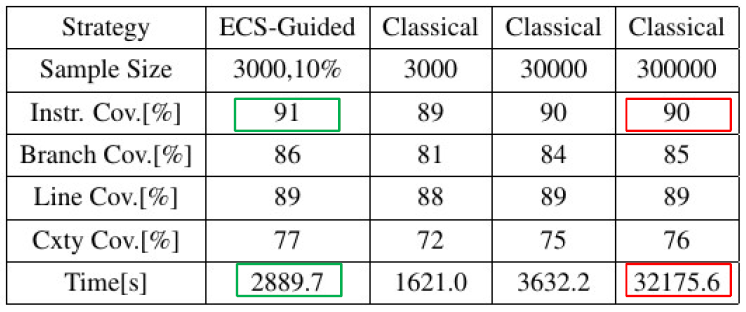
进一步地,相比上一个实验中对所有样本数量进行 x10,x100,基于可解置信度报告搜索策略的帮助下,在仅用 3000 样本,但是设置 ECS 阈值 10% 的情况下,MLB 的覆盖度超过了采样点全部设为30万的情况,且耗时大为降低。
总结与展望
总而言之,在这个工作中,我们提出了一种基于机器学习约束求解的一套符号执行框架(MLBSE)。在真实系统,尤其是大型复杂系统中,使用我们的工具,无需展开主函数外的代码实现,仅通过采样-确认-反馈的形式往下执行,可对传统方法无法支持的非线性计算、库函数调用等复杂代码进行测试,在实验效果和效率上都表现很好。整体而言,我们这个工作的内容如下:
一种基于机器学习约束求解的符号执行框架 MLBSE
采用机器学习优化算法作为底层的约束求解器
能处理复杂数值计算和函数调用的真实程序
基于 MLBSE 的符号执行功能增强
黑盒执行模式
可解置信度报告:供用户参考是否投入更多计算资源
基于可解置信度报告的搜索策略
实现和实验
实现了一个基于机器学习约束求解的符号执行工具 MLB
参数易配置,无须用户修改代码
实验表明相比现有符号执行工具,MLB 在效果和效率上都表现更好
MLB 的增强功能可以有效提高真实程序上符号执行的效率
以上。
参考
[1] Tillmann, N., & Halleux, J. D. (2008, April). Pex–white box test generation for. net. In International conference on tests and proofs (pp. 134-153). Springer, Berlin, Heidelberg
[2] Moura, L. D., & Bjørner, N. (2008, March). Z3: An efficient SMT solver. In International conference on Tools and Algorithms for the Construction and Analysis of Systems (pp. 337-340). Springer, Berlin, Heidelberg.
[3] Sen, K., & Agha, G. (2006, August). CUTE and jCUTE: Concolic unit testing and explicit path model-checking tools. In International Conference on Computer Aided Verification (pp. 419-423). Springer, Berlin, Heidelberg.
[4] Păsăreanu, C. S., Rungta, N., & Visser, W. (2011, July). Symbolic execution with mixed concrete-symbolic solving. In Proceedings of the 2011 International Symposium on Software Testing and Analysis (pp. 34-44).
[5] Souza, M., Borges, M., d’Amorim, M., & Păsăreanu, C. S. (2011, April). Coral: Solving complex constraints for symbolic pathfinder. In NASA Formal Methods Symposium (pp. 359-374). Springer, Berlin, Heidelberg.
[6] Dinges, P., & Agha, G. (2014, November). Solving complex path conditions through heuristic search on induced polytopes. In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering (pp. 425-436).
[7] Bu, L., Liang, Y., Xie, Z., Qian, H., Hu, Y. Q., Yu, Y., ... & Li, X. (2021). Machine learning steered symbolic execution framework for complex software code. Formal Aspects of Computing, 33(3), 301-323.
[8] Y. Yu, H. Qian, and Y.-Q. Hu. Derivative-free optimization via classification. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, pp. 2286– 2292, Phoenix, AZ, 2016.