排序的概念及意义
本章内容我们采用C语言完成代码。
排序的概念
我们先来了解一下基础概念:
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起
来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记
录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍
在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据
的排序
了解完基本概念以后,为了便于理解,我们来举几个生活中的例子:
排序运用
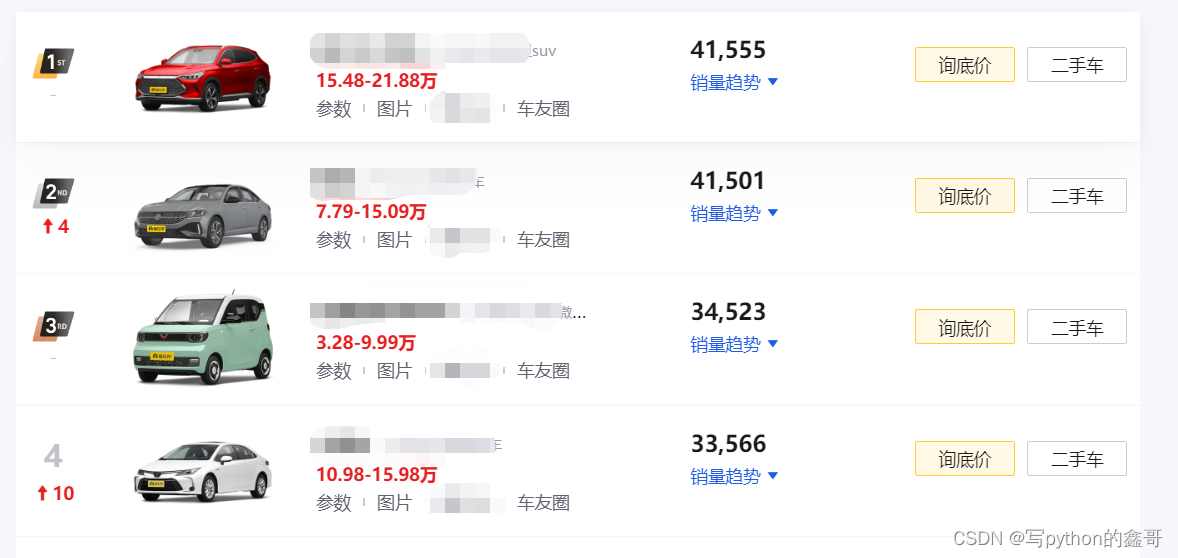
下图是我们常用的购物软件,当我们购买选择商品时不可避免的要给商品排序。

示例一
又比如小伙伴们高考之后,分数太高,纠结于哪所大学,那么下图可以给我们答案。

示例二
插入排序
基本思想
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐
个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想
原理
如图所示:
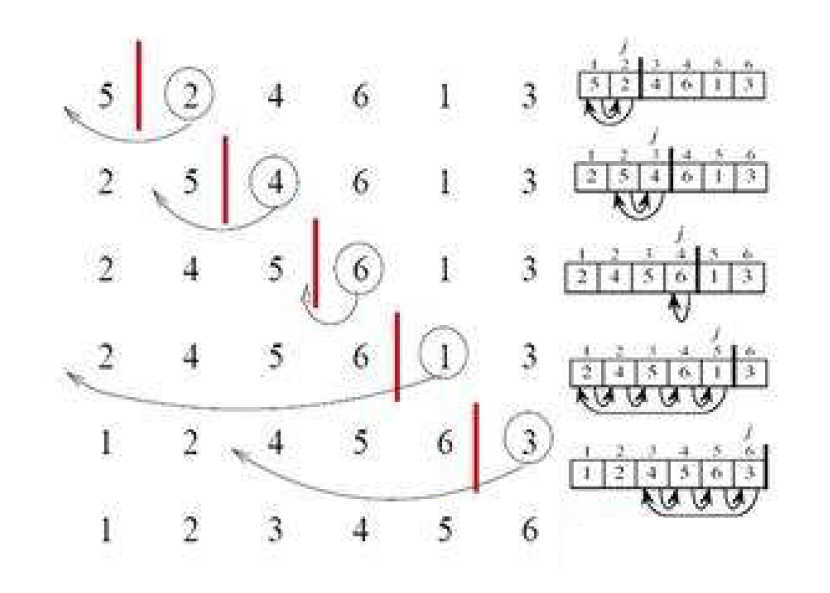
规律
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
实现
void InsertSort(int* a, int n)
{
// [0, end]有序 end+1位置的值插入[0, end],让[0, end+1]有序
for (int i = 0; i < n - 1; ++i)
{
int end = i;
//后一个值保存起来
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}希尔排序( 缩小增量排序 )
定义
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有
记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重
复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。

希尔排序
特性总结
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的
了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的
对比。
比特就业课
3. 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N^1.3—
N^2)
4. 稳定性:不稳定
实现
其实跟前面的插入排序有异曲同工之妙,我们可以把插入排序中的gap看成一
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//gap = gap / 2; // logN
gap = gap / 3 + 1; // log3N 以3为底数的对数
// gap > 1时都是预排序 接近有序
// gap == 1时就是直接插入排序 有序
// gap很大时,下面预排序时间复杂度O(N)
// gap很小时,数组已经很接近有序了,这时差不多也是(N)
// 把间隔为gap的多组数据同时排
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}注意:gap最好不要用固定值。但是要注意,如果为gap/3就要考虑能否被整除。
这里代码实现过程可能与小伙伴们想的有点不一样。

如图,‘9’跟‘4’换了之后,就直接‘1’和‘8’相比,也就是说这个是直接换完一组,然后接着换另外一组,直至换完。
测试
打印函数
我们可以设计出一个打印函数,这样可以方便我们测试。
//打印
void Print(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}测试排序
然后放入测试函数,我们首先测试一下插入排序:
void TestInsertSort1()
{
int a[] = { 2,1,5,6,9,3,7,8 };
InsertSort(a, sizeof(a) / sizeof(int));
Print(a, sizeof(a) / sizeof(int));
}结果:

再来测试一下希尔排序:
void TestInsertSort2()
{
int a[] = { 2,1,5,6,9,3,7,8 };
ShellSort(a, sizeof(a) / sizeof(int));
Print(a, sizeof(a) / sizeof(int));
}结果:

测试排序的性能
我们在测试速度的时候,可以讲vs中的解决方案配置从原来的Debug调成 Release。
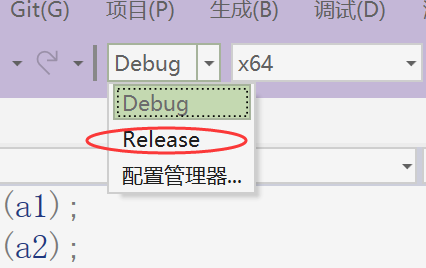
在学习C语言的时候就已经提过,Release可以更加方便的完成计算。
// 测试排序的性能对比
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
free(a1);
free(a2);
}总结
我们用C语言与小伙伴们以探讨了基础的插入排序和更加便捷的希尔排序,从而对排序有了一个基础的认知。
欢迎大家点赞和收藏。