BRDF : 双向反射分布函数(Bidirectional Reflectance Distribution Function)

描述从某个方向入射的能量反射到不同的方向上的能量的分布。

理解反射

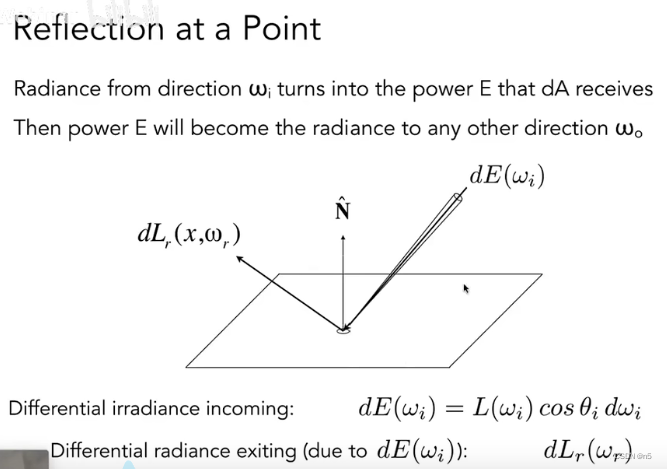
从能量的角度理解反射。上图中，${\omega }_i$方向入射的光线具有的Radiance，累积在微小面积$dA$上，累积为Irradiance。然后E向各个${\omega }_o$方向发射出去，计算反射光线的Radiance。

即上图中下面的两个公式：
1）入射的微分irradiance: $dE{\omega }_i$是入射的Radiance $L({\omega }_i)$乘以微分立体角$d{\omega }_i$和$cos{\theta }_i$
2) 反射的微分Radiance: 是$d{L}_r({\omega }_r)$

而BRDF就是各方向反射的Radiance和入射的总的Irradiance的比例。即，在给定的入射方向上，各个反射方向的Radiance分别占总的入射产生的Irradiance的比例。因此是双向和反射分布。

BRDF定义

BRDF描述的是如何把一个方向入射的能量反射到各个方向去。
再看一下上面的BRDF公式：

• 分子部分是某个反射方向${\omega }_r$的Radiance的微分
• 分母部分是某个入射方向${\omega }_i$的Irradiance的微分。由于Irradiance是各个方向的Radiance累积起来的。因此这儿通过考察一个微小的微分立体角$d{\omega }_i$,这个Irradiance的微分就是入射的Radiance和微分立体角的乘积，以及为了投影受光表面还乘了$cos{\theta }_i$。
  另外Radiance和Irradiance都是针对单位投影面积的。

BRDF定义了不同的材质

BRDF描述了光线和物体是如何作用的。

反射方程 The Reflection Equation

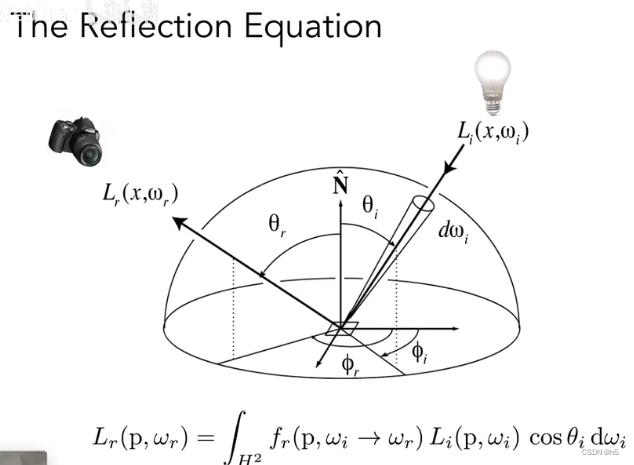
反射方程计算的是对于某个着色点P的任意一个反射方向${\omega }_r$的Radiance。方法是将这个着色点接受到的Irradiance的微分，即：

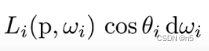
乘上BRDF，即：

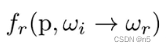
然后在半球上，针对入射方向${\omega }_i$进行积分。

BRDF本身就是反射radiance和入射Irradiance的比例，所以这个方程很自然。
如果直接把BRDF的定义式代入到反射方程中，BRDF的分母部分就会和方程内的入射Irradiance微分消掉，得到的就是反射的Irradiance。

我觉得核心是BRDF可以在某个着色模型下去定义好计算好，然后应用到反射方程中计算反射。

挑战：反射方程是递归的

• 入射的Radiance不仅仅来自于光源，也可以来自于反射后的光线
• 入射radiance依赖于其他地方反射过来的radiance

渲染方程 The Rendering Equation

• 反射方程只考虑了反射的光，没考虑物体自己会发光
• 反射方程加上物体自发光的 Radiance 就是渲染方程
• 方程中所有的方向都是从着色点向外
• 积分域为半球，写作$\Omega +$或$H^2$。因为下半球过来的光打在背面不能照亮表面。
• $cos$项使用点积表示
• 通过一个方程表示所有的光线传输
• 所有限制在物体表面上的光线传输都是满足渲染方程

理解渲染方程

一个点光源时

有很多点光源时

• 将入射光加起来

如果是面光源

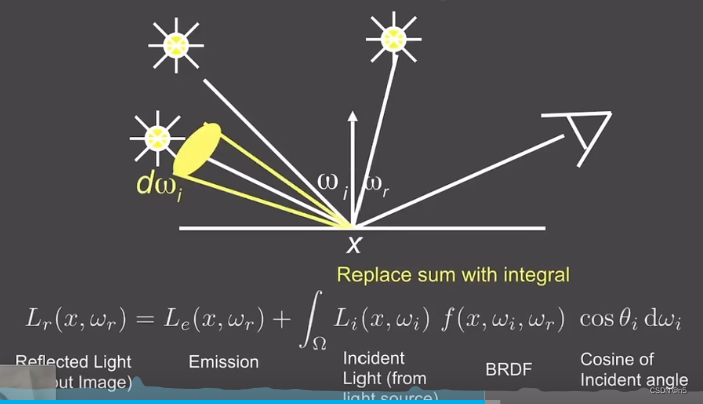
• 面光源是一堆点光源的集合，将面光源上各个点的贡献积分起来
• 使用积分代替求和

如果是其他物体上反射过来的Radiance

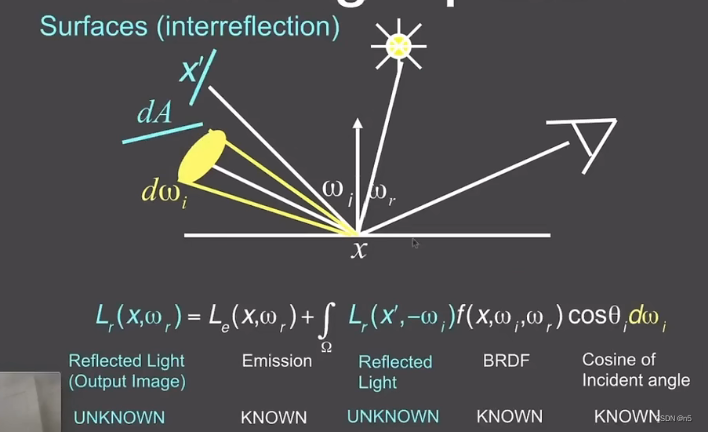
• 将反射面当成光源
• 将反射到$-{\omega }_i$的Radiance当成入射的Radiance

将渲染方程看做递归的方程

图中第二个公式是对渲染方程的简写

• u, v表示两个不同的着色点位置
• l(u)表示位置u处反射出的光
• e(u)表示位置u的自发光
• l(v)表示位置v处反射出的光
• K(u,v)dv表示从各个不同的位置v有多少光反射到位置u

使用算子进一步简写

• L表示反射出的能量，要算的
• E表示光源发出的能量
• K是一个反射操作符
• 这么写可以离散化为简单的矩阵方程
  
• 这个矩阵的形式可以推导出L
• 将(I-K)的逆矩阵展开
  
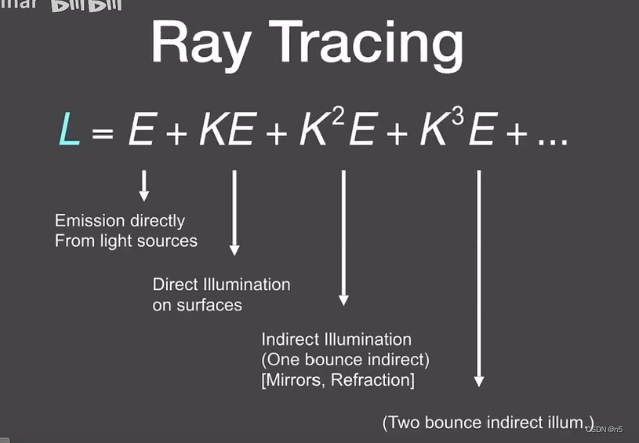
  以上推导难以理解是因为简化了很多中间过程