设置顶点集合S并不断地作贪心选择--（不属于这个集合S中距离"源"最短的顶点）来扩充这个集合--更新最短距离

这张图需要放在最前面，就是经典dijkstra的主要思想。

为什么这样贪心是对的？

1、问题描述

给定带权有向图G =(V,E)，其中每条边的权是非负实数。另外，还给定V中的一个顶点，称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。

2、Dijkstra算法

Dijkstra算法是解单源最短路径问题的贪心算法。

其基本思想是，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其他顶点之间的最短路径长度。

Dijkstra算法可描述如下，其中输入带权有向图是G=(V,E)，V={1,2,…，n}，顶点v是源。c是一个二维数组，c[i][j]表示边(i,j)的权。当(i,j)不属于E时，c[i][j]是一个大数。dist[i]表示当前从源到顶点i的最短特殊路径长度。在Dijkstra算法中做贪心选择时，实际上是考虑当S添加u之后，可能出现一条到顶点的新的特殊路，如果这条新特殊路是先经过老的S到达顶点u,然后从u经过一条边直接到达顶点i，则这种路的最短长度是dist[u]+c[u][i]。如果dist[u]+c[u][i]<dist[i]，则需要更新dist[i]的值。

步骤如下：

(1) 用带权的邻接矩阵c来表示带权有向图, c[i][j]表示弧<vi,vj>上的权值。

设S为已知最短路径的终点的集合,它的初始状态为空集。

从源点v经过S到图上其余各点vi的当前最短路径长度的初值为：dist[i]=c[v][i], vi属于V.

(2) 选择v u, 使得dist[u]=Min{dist[i] | vi属于V-S},vj就是长度最短的最短路径的终点。令S=S U {u}.

(3) 修改从v到集合V-S上任一顶点vi的当前最短路径长度:如果 dist[u]+c[u][j]< dist[j] 则修改 dist[j]= dist[u]+c[u][j].

(4) 重复操作(2),(3)共n-1次.

伪代码如下：显然没有第一张图片清晰易懂

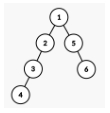
举例子：对右图中的有向图，应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下页的表中。

代码：

//4d5 贪心算法 单源最短路径问题
#include <iostream> 
#include <fstream>  
#include <string> 
using namespace std; 
 
const int N = 5;
const int M = 1000;
ifstream fin("4d5.txt"); 
 
template<class Type>
void Dijkstra(int n,int v,Type dist[],int prev[],Type c[][N+1]);
void Traceback(int v,int i,int prev[]);//输出最短路径 v源点，i终点
 
int main()
{
	int v = 1;//源点为1
	int dist[N+1],prev[N+1],c[N+1][N+1];
 
	cout<<"有向图权的矩阵为："<<endl;
	for(int i=1; i<=N; i++)
	{
		for(int j=1; j<=N; j++)
		{
			fin>>c[i][j];    
            cout<<c[i][j]<<" ";  
		}
		cout<<endl;
	}
 
	Dijkstra(N,v,dist,prev,c);
 
	for(int i=2; i<=N; i++)
	{
		cout<<"源点1到点"<<i<<"的最短路径长度为:"<<dist[i]<<"，其路径为";
		Traceback(1,i,prev);
		cout<<endl;
	}
 
	return 0;
}
 
 
template<class Type>
void Dijkstra(int n,int v,Type dist[],int prev[],Type c[][N+1])
{
	bool s[N+1];
	for(int i=1; i<=n; i++)
	{
		dist[i] = c[v][i];//dist[i]表示当前从源到顶点i的最短特殊路径长度
		s[i] = false;
 
		if(dist[i] == M)
		{
			prev[i] = 0;//记录从源到顶点i的最短路径i的前一个顶点
		}
		else
		{
			prev[i] = v;
		}
	}
 
	dist[v] = 0;
	s[v] = true;
 
	for(int i=1; i<n; i++)
	{
		int temp = M;
		int u = v;//上一顶点
 
		//取出V-S中具有最短特殊路径长度的顶点u
		for(int j=1; j<=n; j++)
		{
			if((!s[j]) && (dist[j]<temp))
			{
				u = j;
				temp = dist[j];
			}
		}
		s[u] = true;
 
		//根据作出的贪心选择更新Dist值
		for(int j=1; j<=n; j++)
		{
			if((!s[j]) && (c[u][j]<M))
			{
				Type newdist = dist[u] + c[u][j];
				if(newdist < dist[j])
				{
					dist[j] = newdist;
					prev[j] = u;
				}
			}
		}
	}
}
 
//输出最短路径 v源点，i终点
void Traceback(int v,int i,int prev[])
{
	if(v == i)
	{
		cout<<i;
		return;
	}
	Traceback(v,prev[i],prev);
	cout<<"->"<<i;
}

input:

1000 10 1000 30 100
1000 1000 50 1000 1000
1000 1000 1000 1000 10
1000 1000 20 1000 60
1000 1000 1000 1000 1000

output: