题目描述

小 C 非常喜欢树。上次后院的蚂蚁看腻了，这次准备来观察树。

小 C 每天起得早早的，给小树浇水，并且每天记录这棵小树的一些数据。树在小 C 的精心呵护下不断长大。经过若干天的记录，小 C 竟然发现了一棵树生长的规律！

为了阐述其规律，小 C 想先使用一种严谨的语言来抽象化一棵树。

首先，小 C 用图论的概念定义了一棵树 $T =< V, E >$ ， $V$ 表示所有点构成的集合， $E$ 表示所有边（无向边）构成的集合。一棵具有一定形态的树用一个大写字母简记，一般会使用 $T$ ；其大小等于 $∣ V ∣$ ，即节点的个数。

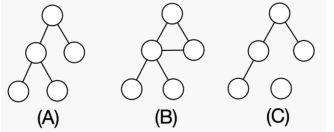
小 C 发现所有树都有一个共同点：大小为 $n$ 的树，恰好含有 $n - 1$ 条边，并且任意两个节点间存在路径使得互相可达。比如说下图中 (A) 是一棵树，而 (B)© 却不是。

自然界中所有树都有根，对于树 $T$ 也有且仅有一个根，其为 $V$ 中的某个节点 $r$ 。于是小 C 可以对所有节点定义深度，节点 $u$ 的深度等于 $u$ 到 $r$ 的距离 $+ 1$ ，例如下面这棵树中，令节点 $1$ 为根 $r$ ，则节点 $2$ 、 $3$ 的深度为 $2$ ，节点 $4$ 、 $5$ 的深度为 $3$ ，而节点 $1$ 自身的深度为 $1$ 。

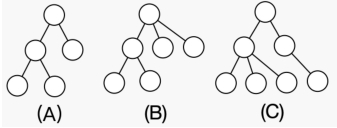
由此可以看出，抽象出来的树和现实中的树正好上下颠倒了。接下来小 C 开始定义生长。某次生长操作用 $T = g ro w (T ’, d)$ 表示， $T ’$ 表示生长前的树， $T$ 表示生长之后的树。成长规律根据参数 $d$ 决定。生长时， $T ’$ 中所有深度为 $d$ 的节点同时增加一个新的节点与之连接，得到的树即为 $T$ 。比如说下图中 (A) 为原树 $T$ ，(B) 为 $g ro w (T, 1)$ ，© 为 $g ro w (T, 2)$ 。

小 C 又定义成长，表示一棵树经过一系列生长得到另一棵树的过程。令原树为 $T_0$ ，总共 $k$ 次生长操作，第 $i$ 次生长的参数为 $d_i$ ，则可以表示为：

$T_1 = grow(T_0 ,d_1 ) → T_2 = grow(T_1 ,d_2 ) → ··· → T_k = grow(T_{k−1} ,d_k )$
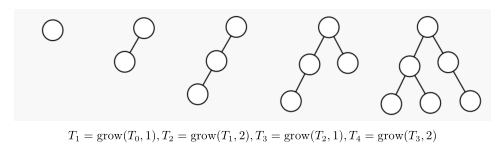
小 C 又定义种子为大小为 11、仅包含根节点的树。下图是一颗种子的成长过程。

然而一个猜想需要诸多事实来支撑。小 C 又观察了许多棵树，然而树儿都长大了，小 C 只能得到成长之后的树 $T$ 。他想知道对于一颗种子，存不存在某种成长过程，使得种子能长成树 $T$ 。于是小 C 把问题交给了你。

本题每个输入文件有多组测试数据

输入格式

从文件 observe.in 中读取数据。第一行一个正整数 $Q$ ，表示数据组数。

对于每组数据，将会描述一棵成长之后的树 $T$ ；

每组数第一行两个正整数 $n$ 和 $r$ ，表示树 $T$ 的大小、 $T$ 的根，节点依次从 $1$ 到 $n$ 标号；

接下来 $n - 1$ 行，每行两个整数 $u$ 和 $v$ ，描述一条边 $(u, v)$ 。

保证 $T$ 一定是一棵合法的树。

输出格式

输出到文件 observe.out 中。总共 $Q$ 行，每行表示对应的树 $T$ 是否存在成长过程，使得种子成长成 $T$ ，如果存在，输出 Yes，否则输出 No（请注意大小写）。

样例

输入数据#1

输出数据#1

Yes

解释#1

这棵树的形态如下。

此为题面描述的成长过程中的例子。

输入数据#2

输出数据#2

No

解释#2
这棵树的形态如下。

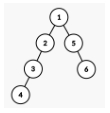
一颗种子不存在某种成长方式变成这棵树。

输入数据#3

输出数据#3

Yes
No

样例4-5
请下载附件查看（附件）。

数据范围
$10\% 的数据：n≤5。$
$30\% 的数据：n≤10。$
$50\% 的数据：n≤100。$
$对于 70\% 的数据：n≤3×10^3 。$
$对于 100\% 的数据：1 ≤ Q ≤ 10，1 ≤ n ≤ 10^51≤r≤n。$

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
struct node{
    vector<int> cls;
    int p;
    int n1,n2;//n1表示孩子结点数，n2表示孩子中的叶子结点数
}trees[N];
vector<int> deeps[N];//树结点深度
int nums[N];//标记深度为i的叶子结点数
priority_queue<int,vector<int>,greater<int> > ns;//小根堆，元素小的优先级高，注意这里的写法都是固定的
 
void dfs(int root,int d){
    for (int i = 0; i < trees[root].cls.size() ; ++i) {
        dfs(trees[root].cls[i], d+1);
    }
    //叶子结点
    if(trees[root].cls.empty()){
        trees[trees[root].p].n2++;//父结点的叶子结点数++
        nums[d]++;//标记深度为d的叶子结点数
        if(nums[d] == 1){//首次放入优先队列中
            ns.push(d);//按叶子优先级
        }
    }else{//非叶子结点加入deeps中
        deeps[d].push_back(root);
    }
} 
 
int main(){
    freopen("observe.in","r",stdin);
    freopen("observe.out","w",stdout); 
    int q;
    scanf("%d",&q);
    while (q--){
        int n,r;
        scanf("%d%d",&n,&r);
        memset(trees,0, sizeof(trees));
        memset(deeps,0, sizeof(deeps));
        memset(nums,0, sizeof(nums));
        ns = priority_queue<int,vector<int>,greater<int> > ();
 
        int u,v;
        for (int i = 1; i <= n - 1 ; ++i) {//n-1条边
            scanf("%d%d",&u,&v);
            trees[u].cls.push_back(v);
            trees[v].p = u;
            trees[u].n1 ++ ;
        }
        dfs(r,1);
        if(nums[n]){//说明是单链
            printf("Yes\n");
            continue;
        }
        while(!ns.empty()){
            int d = ns.top();//叶子结点深度是d，需要从d-1层结点开始删除
            int size = deeps[d - 1].size();
 
            if(size > nums[d]){//如果父结点数比当前的子结点数多，肯定不满足条件，直接输出No
                printf("No\n");
                break;
            }
            vector<int> newleaf;
 
            int flag = 0;
            for (int i = 0; i < deeps[d - 1].size(); ++i) {
                int x = deeps[d - 1][i];
                if(!trees[x].n2){//某个结点没有叶子结点，不满足条件
                    flag = 1;
                    break;
                }else{
                    trees[x].n1 --;
                    trees[x].n2 --;
 
                    if(x != r && trees[x].n1 == 0){//变成了叶子结点了,先缓存起来,注意 根结点不用管了
                        newleaf.push_back(i);//记录下标，防止遍历复杂度
                    }
                }
            }
            if(flag){
                printf("No\n");
                break;
            }
            if(size == nums[d]){
                ns.pop();
            }
            nums[d] -= size;//剪去叶子结点
            //处理新产生的叶子结点
            for (int i = newleaf.size() - 1; i >= 0 ; i--) {
                nums[d-1] ++ ;
                if(nums[d-1] == 1){
                    ns.push(d-1);//产生了新深度的叶子
                }
                int t = newleaf[i];
                int q = deeps[d-1][t];
 
                trees[trees[q].p].n2 ++ ;
                //对应deeps 要 删除该结点
                deeps[d-1].erase(deeps[d-1].begin() + t);
//                for (int j = 0; j < deeps[d-1].size() ; ++j) {
//                    if(deeps[d-1][j] == t){//该元素已经变为叶子了，删除
//                        deeps[d-1].erase(deeps[d-1].begin() + j);
//                        break;
//                    }
//                }
            }
        }
        if(ns.empty()){
            printf("Yes\n");
        }
    }
    return 0;
}