✍个人博客:https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
📣专栏定位:为 0 基础刚入门数据结构与算法的小伙伴提供详细的讲解,也欢迎大佬们一起交流~
📚专栏地址:https://blog.csdn.net/Newin2020/article/details/126445229
❤️如果有收获的话,欢迎点赞👍收藏📁,您的支持就是我创作的最大动力💪
🎏唠叨唠叨:在这个专栏里我将会整理 PAT 甲级的真题题解,并将他们进行分类,方便大家参考。
差分
前面我们讲到了前缀和算法,这一讲我们来看看前缀和的逆运算即差分算法是什么,在有些题中需要我们对一个区间上的所有数进行加减操作,如果通过循环一个个加减时间复杂度会很高,这时差分算法就派上用场了,下面我们来看看差分是如何解决这类问题的,并且会进行小小的扩展,延伸到差分矩阵问题的解决。
Tips:不用被差分这么名字所吓到,其实真正学起来并不会特别难理解,相信你一定能快速掌握~
原理
假设给定一个原数组 a,那么差分数组 b 的存在就是使得如下公式成立:
a [ i ] = b [ 1 ] + b [ 2 ] + . . . + b [ i ] a[i]=b[1]+b[2]+...+b[i] a[i]=b[1]+b[2]+...+b[i]
而上面的公式,是由差分数组 b 推导而来:
b [ 1 ] = a [ 1 ] b[1]=a[1] b[1]=a[1]
b [ 2 ] = a [ 2 ] − a [ 1 ] b[2]=a[2]-a[1] b[2]=a[2]−a[1]
b [ 3 ] = a [ 3 ] − a [ 2 ] b[3]=a[3]-a[2] b[3]=a[3]−a[2]
. . . ... ...
b [ n ] = a [ n ] − a [ n − 1 ] b[n]=a[n]-a[n-1] b[n]=a[n]−a[n−1]
将上面公式两两相加,消除完后就可以得到 a[i] 的公式了。
因此我们称 a 为 b 的前缀和,而 b 为 a 的差分。
差分
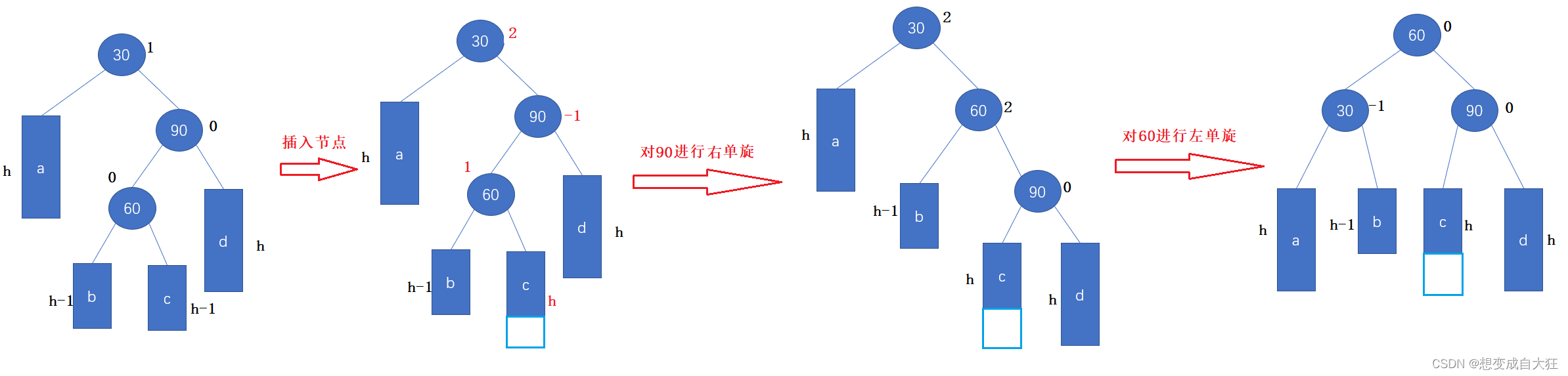
现在我们来看如何将差分数组模拟出来,现在给定一个区间 [l,r],我们希望在这个区间上面的每个数都加上一个 c,如果直接循环添加每个数时间复杂度会很大。而利用差分加前缀和的方法,就可以使效率提高很多,至于如何操作直接上图解,首先初始化一个差分数组 b 并且数组中的元素一开始都为 0。

现在执行上述操作,假设在 [3,6] 这个区间上的每个数都加上 1,则可以在下标为l 的地方加上 c,在下标为 r+1 的地方减去 c,操作后结果如下:

这时候我们再对数组 b 计算前缀和数组 a 就可以得到一个非常奇妙的结果,居然前缀和数组就是最终我们要得到的数组,这其实就是利用了上面的公式。
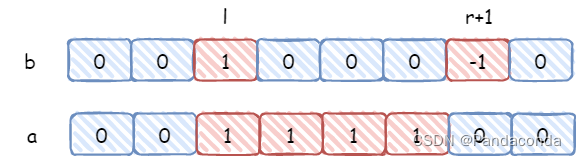
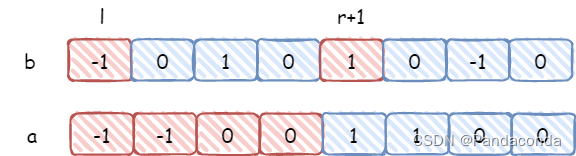
我们再执行一个操作,在区间 [1,4] 上的每个数都减去 1,其实就和上面操作一样,只是在下标 l 处加上了一个负数,在下标 r 处减去一个负数。
接着来看一道模板题,就是对区间上的数进行加减操作。
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n1,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000输入样例:
6 3 1 2 2 1 2 1 1 3 1 3 5 1 1 6 1输出样例:
3 4 5 3 4 2
可以发现,和我们上面讲的例子一模一样,只是这里要多一个初始化操作,上面的图解我们将 b 中的元素都初始化为 0 。而在这道题中预先给定了一个数组,需要我们先将这个数组初始化到 b 上,例如给定第一个数为 1,则在下标 l=1 和 r+1=2 处分别加上 1 和 -1;第二个数为 2 ,则在下标 l=2 和 r+1=3 处分别加上 2 和 -2,以此类推。
初始化之后,再进行区间的加减操作,这也和我们上面一样,直接来看代码。
#include <bits/stdc++.h>
using namespace std;
int n, m, a[100005], b[100005];
//差分操作
void Add(int c, int l, int r) {
b[l] += c;
b[r + 1] -= c;
}
int main() {
scanf("%d %d", &n, &m);
//初始化数组b
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
Add(a[i], i, i);
}
//进行区间加减操作
while (m--) {
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
Add(c, l, r);
}
//通过计算b的前缀和还原出目标
for (int i = 1; i <= n; i++) {
b[i] += b[i - 1];
printf("%d ", b[i]);
}
return 0;
}
差分矩阵
有前缀和矩阵,自然就有差分矩阵,不过做法和一维的差分十分类似,有前面的铺垫再来看这个就不难理解了,还是通过例子来讲,现在假设有一个 3×4 的矩阵,而差分矩阵 b 中的元素全部初始化为 0。
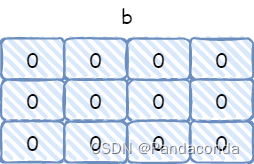
现在假设给定两个坐标 (1,1) 和 (2,2) 分别表示我要指定的子矩阵的左上角和右下角,然后我想要将这个子矩阵中的所有元素都加上 1。那么我们就需要在四个地方进行修改(下面中的每条公式修改范围都对应了其下图中红色区域):
-
b [ x 1 ] [ y 1 ] + = c b[x1][y1]+=c b[x1][y1]+=c,相当于包括
(x1,y1)在内的右下区域都加上了c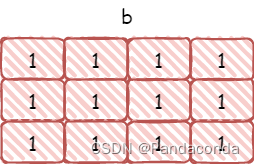
-
b [ x 2 + 1 ] [ y 1 ] − = c b[x2+1][y1]-=c b[x2+1][y1]−=c,相当于包括
(x2+1,y1)在内的右下区域都减去了c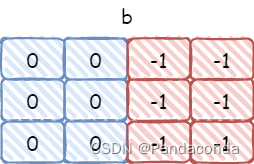
-
b [ x 1 ] [ y 2 + 1 ] − = c b[x1][y2+1]-=c b[x1][y2+1]−=c,相当于包括
(x2,y1+1)在内的右下区域都减去了c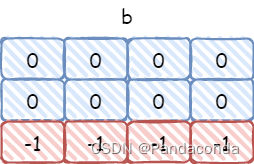
-
b [ x 2 + 1 ] [ y 2 + 1 ] + = c b[x2+1][y2+1]+=c b[x2+1][y2+1]+=c,相当于包括
(x1+1,y1+1)在内的右下区域都加上了c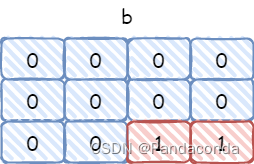
先别着急,我们来看看执行后的效果如何。
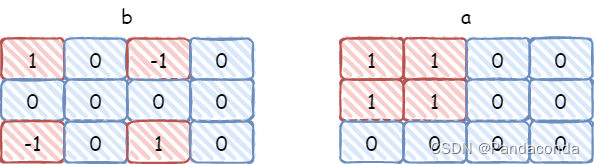
可以惊讶的发现,计算完子矩阵前缀和后,居然就是我们想要得到的矩阵,这其实就和子矩阵前缀和运算的性质有关,其计算公式如下:
b [ i ] [ j ] + = b [ i − 1 ] [ j ] + b [ i ] [ j − 1 ] − b [ i − 1 ] [ j − 1 ] b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1] b[i][j]+=b[i−1][j]+b[i][j−1]−b[i−1][j−1]
可以发现相对于正常的子矩阵前缀和运算少加了一个 a[i][j],这是因为差分一开始已经进行了初始化操作,每个位置上初始的值都已经加到差分数组 b 中了,我们只用管修改操作即可。
另外,这部分差分的操作和前缀和的操作和其实有点类似,都需要对重复的部分进行操作。前缀和是因为多加了一次重复区域而要减去重复的部分,而差分则是多减了一次重复区域而加上重复的部分,大家可以将上述公式带入到图中矩阵进行验证,发现能够完全对应的上。
对前缀和二维运算不太熟悉或没有接触过的小伙伴可以跳转到我之前的文章,传送门如下:
【C++算法图解专栏】一篇文章带你掌握前缀和算法(一维+二维)
讲完了上述原理,下面这道模板题都没有问题啦!
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000−输入样例:
3 4 3 1 2 2 1 3 2 2 1 1 1 1 1 1 1 2 2 1 1 3 2 3 2 3 1 3 4 1输出样例:
2 3 4 1 4 3 4 1 2 2 2 2
可以发现和一维的差分很类似,本地都给了初始的数组,需要我们先对差分数组 b 进行初始化,比如 (1,1) 的下标处初始值为 1,将传入的左上角坐标和右上角坐标都设置相同的坐标 (1,1),这样就相当于在 (1,1) 处加上了值 1,其它情况类似。
初始化完后,再进行区间的加减操作,代码如下:
#include<iostream>
using namespace std;
int n, m, q, a[1010][1010], b[1010][1010];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
scanf("%d%d%d", &n, &m, &q);
//初始化差分数组
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
scanf("%d", &a[i][j]);
insert(i, j, i, j, a[i][j]);
}
}
//对区间进行加减
while (q--)
{
int x1, x2, y1, y2, c;
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
insert(x1, y1, x2, y2, c);
}
//计算前缀和
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
//子矩阵前缀和计算要减去重复的部分
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
printf("%d ", b[i][j]);
}
printf("\n");
}
return 0;
}
总结
恭喜您成功点亮差分算法技能点!
在平时做题的过程中,差分和前缀和两个算法经常会一起出现,前缀和可以没有差分,但差分往往不能没有前缀和,因为差分数组只是记录了区间的操作,还需要前缀和将数组还原出来。
在一开始学差分的时候,往往会被这个名字给吓退,但其实理解起来没有这么难,在平时算法题中一般也只会是一个零件,比如一些题中需要对区间上的数进行加减操作,这时就要想到可以用差分来解决。