相比于算法目标的复杂，算法步骤却异常的简单，下面具体介绍利用 SeamCarving 算法进行图像剪裁的步骤：

1.计算图像中每个像素的“重要程度”（能量），生成能量图。在绝大多数情况下，我们可以做出如下假设：像素值变化越剧烈的区域（如边界，角点），是人眼最容易捕捉到的区域，也是图像相对重要的区域。与此相反，像素变化较为平缓的区域，很多情况下使图像中的“背景区域”，是人们很少关注的区域。所以，算法给出一个简易假设：如果一个像素梯度绝对值较大，则该像素重要，算法倾向于保留。而某像素位置的梯度绝对值接近 0，则该像素不重要，算法倾向于删除。因此，某像素的“重要度”（能量）可由以下公式计算得出：

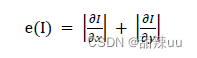
每个像素按照上述公式算出能量值后，构成能量图 E。

1. 从能量图中找到一条能量累积最小的纵向八连通路径，称之为 Seam。

通常在这个步骤中使用动态规划算法，能够使得算法的时间复杂度从 n3^n

（暴力搜索）降低至 n^22。其核心步骤是构建能量累计图 M，其计算方式如下：

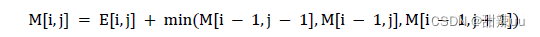
在此同时，记录每一个像素最小能量路径的前置像素。之后，从 M 最后一行找到能量累积最小的像素，从此像素开始，根据前置像素信息回溯到第一行，最终找到一条能量累积最小的纵向连通路径。

3.删除上一步骤中得到的连通路径。

4.重复 1 至 3 步骤，直到删除的列数符合剪裁要求。

5.将图像旋转 90°，重复 1-4 步骤，直到删除的行数符合剪裁要求。

6.将图像旋转回原图方向。对于图像重定向的任务，其核心思路是：首先通过其他方法对原有图像进行等比例放缩（例如双线性插值放大图像），之后在该图像上利用 SeamCarving 进行图像剪裁，即可起到图像重定向的效果。

而对于区域删除的任务，只需要将待删除像素的重要性（能量）特殊标注为 ∞，就能使生成的 Seam 通过待删除区域，不断删除 Seam 直到将目标区域完全删除。同理，对于不想误删的区域，可手动将其重要性（能量）标注为 +∞。

三、算法实现

---

1. 计算能量图

本次实现选取 Sobel 算子计算像素点的梯度，Sobel 算子形式如下：

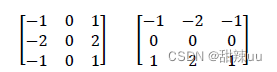
该算子与原图像做卷积，可以得出图像每个像素点的梯度，这就构成了算法描述中提到的能量图，其代码实现如下图：

2.计算能量累积图

生成能量累积图过程中值得注意的问题是，计算时需要时刻记录每个像素在其最小能量连通路径中的前置节点，这样方便在找到最小累积值对应的像素之后，回溯找到整条最小能量连通路径。其实现代码如下所示：

3.找出最小能量连通路径并删除这部分

通过上一步骤中生成的前置节点信息 track，回溯找到最小能量的联通路径，最终对其进行删除，其实现代码如下所示：

4.根据目标图片尺寸对原图进行剪裁。

其实现代码如下:

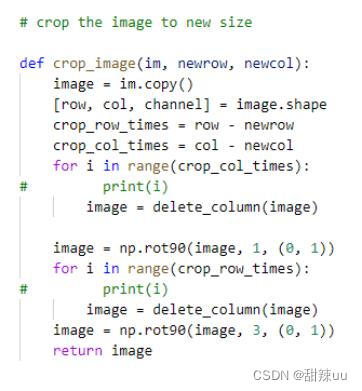
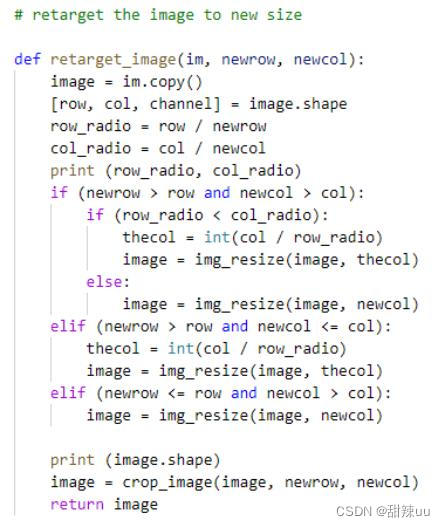
5.图像重定向

实现代码图像的重定向主要针对目标尺寸比原图像尺寸大的情况（若重定向尺寸较原图小，可直接进行图像剪裁）。针对这种情况，首先根据目标尺寸的长宽，适当等比例放大原图像，针对放大后的图像再进行上述的图像剪裁操作，最终完成图像重定向的目标。

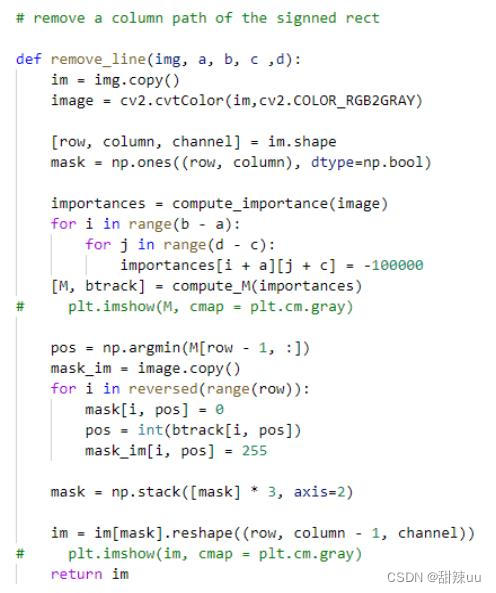
6. 区域删除的实现

1)设定某矩形区域能量值为 ∞，并删除一条最小能量连通路径

2)多次删除连通路径，直到指定区域完全被删除

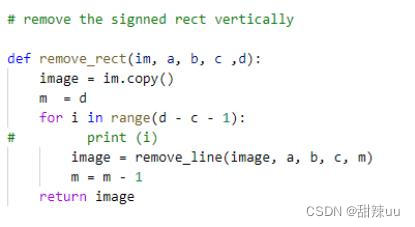
其中值得注意的是，第一个函数是将标定的矩形区域以纵向删除的方式进行去除（一次删除矩形中的一列），而后者则是以横向的方式对选定矩形区域删除（一次删除矩形中的一行）。根据选定目标的不同，两种删除方式得到的结果也有所不同。

四、实验结果与分析

---

1. 中间结果的可视化

1)原图像读取

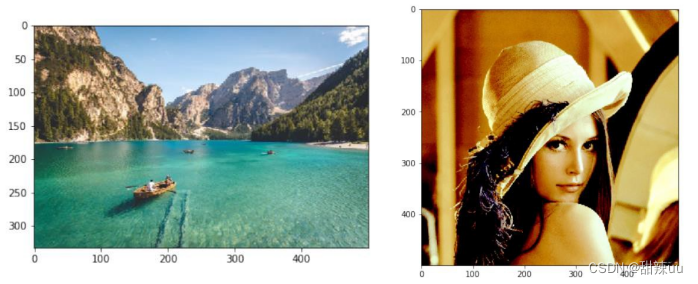
2)能量图

3)能量累积图

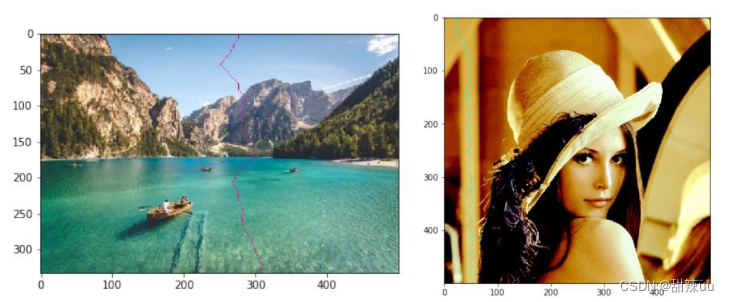
4)找到最小能量连通路径左边图像中使用红色细线标注（中部偏右），右边图像使用绿色细线标注（靠左部分）。

2.图像剪裁

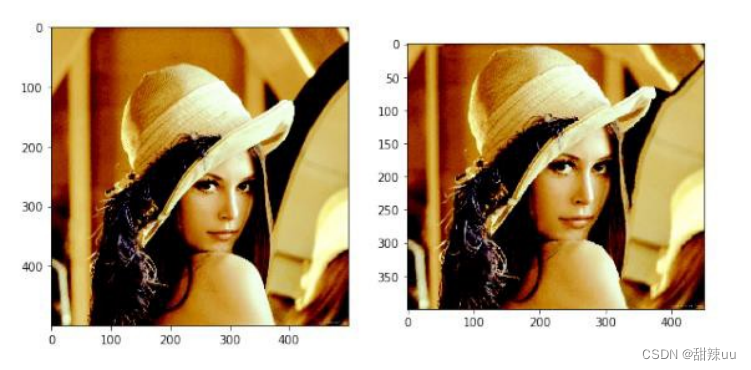
如上图所示，第一幅图像由 333500 像素剪裁为 333300 像素，第二幅图像由 500*500 像素剪裁为 400450 像素。左半部分均为原图像，右半部分图像则是剪裁后的结果。可以看出在上述两种情况下，剪裁前后图像几乎没有发生扭曲和变形。最重要的是，图像中重要的物体和区域（船、人物等）没有因为长宽比例的变化而发生挤压和拉伸。

对于上述情况，将图像由 500500 像素剪裁至 500350 像素。图像变窄的同时人物面部也发生了可见的扭曲和变形，这是由于人物皮肤区域较为平滑，但其位于图像的前景区域，这种情况下不能仅根据像素梯度判断该像素是是否重要。对于前景比例较大或前景区域较为平滑的图像，SeamCarving 通常会得到不理想的结果，这是算法的重要缺陷之一.

3.图像放缩

这部分内容与上一部分相似，仅放出实验结果:

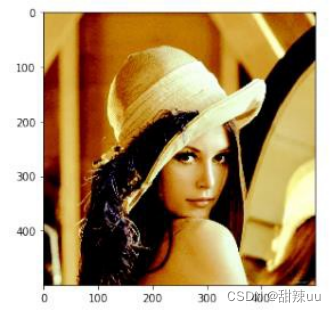
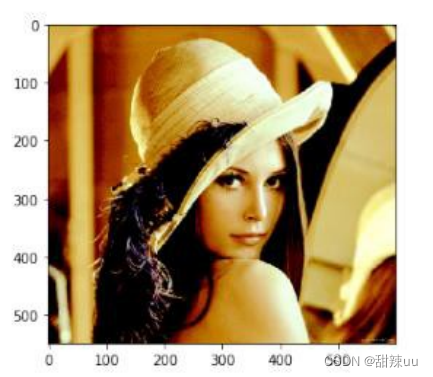
第一幅图由 333500 像素重定向至 320400 像素，第二幅图由 500500 像素重定向至 550600 像素

4.区域删除

本次实验选取某一矩形区域，对其进行删除。左侧图像中待删除的矩形区域标记有蓝紫色蒙版（远方的小船），右侧图像为删除矩形后的图像：

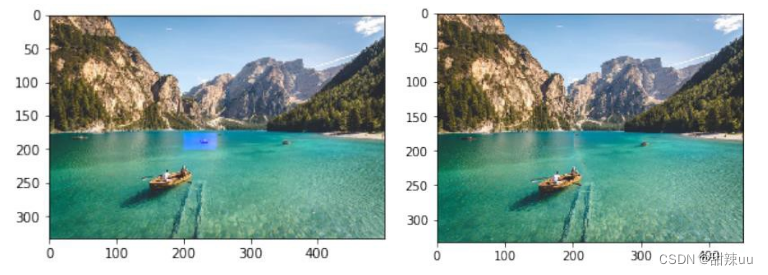
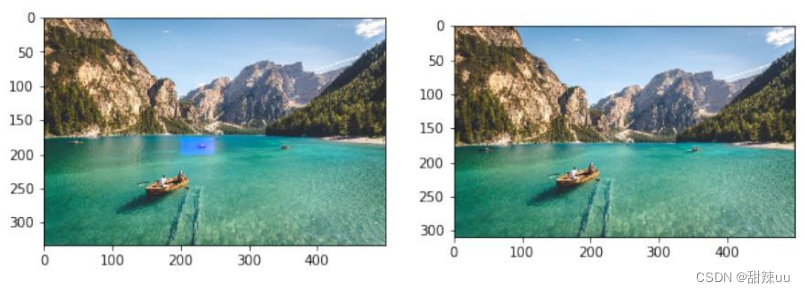
上述两组删除实例中，前者是纵向删除矩形中的像素（一次删除矩形的一列），后者则是横向删除矩形中的像素。所以删除前后，前一副图像的宽度变窄，而后一幅图像的高度降低。但无论是横向删除还是纵向删除，删除后的图像依然没有发生明显的形变与扭曲，保持着良好的稳定性与可视性。

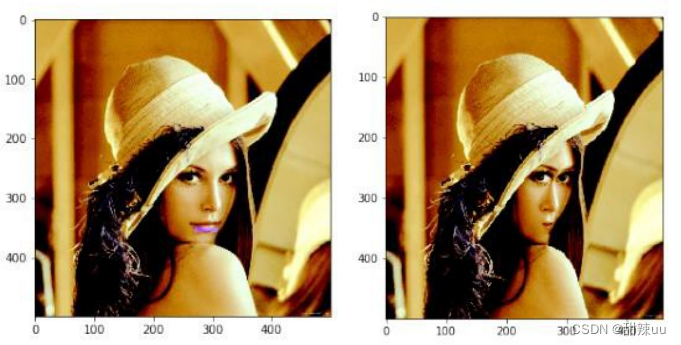
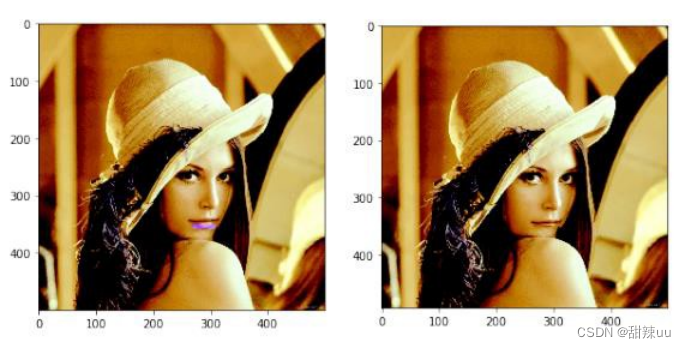
而在以上两组删除实例中，对于图中人脸嘴唇区域的删除，前者采取了纵向删除的方式，而后者采用了横向删除的方式。可以明显地看出，纵向删除的方式极大地扭曲了人脸图像，而横向删除后的图像看上去则比较自然，甚至产生了人物“抿嘴”的效果。所以，针对不同的图像、不同的待删除区域，应该慎重选择删除的策略。

五、尝试与发现

---

1.改变像素重要性评价指标

上文图像剪裁第三组实验中，Lena 图像人脸在经过 SeamCarving 剪裁之后，人脸区域发生扭曲，影响了图像的整体观感。这是由于人的皮肤虽然是图像的前景，但其梯度较为平滑，导致了算法的误删。为了解决这个问题，需要让算法更加“智能”地判断像素的“重要性”，所以，本文尝试增加像素的重要性评价指标，结合前景分离的技术（GrabCut）,提升前景像素的重要性，最终使得图像剪裁更加“智能”。

GrabCut 是迭代的 GraphCut 算法。该算法利用了图像中的纹理（颜色）信息和边界（反差）信息，能够较为迅速地将图像中的前景和背景分离，该算法为每个像素估计其为前景的概率，根据阈值完成图像的像素级分割。

上图是 GrabCut 对 Lena 图像进行前景分离的结果，可以看到算法把前景中的人像较为完整地保留了下来，背景则以黑色像素替代。但是受限于算法的能力，可以看到分离后的图像仍然带有一些背景信息。

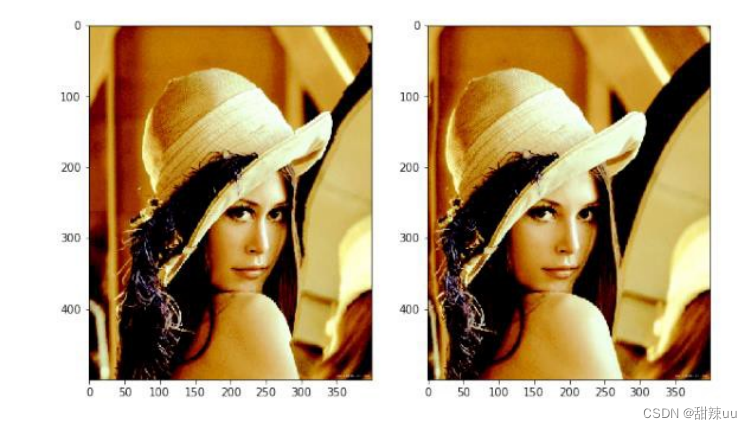
如上图所示，左图为直接利用 SeamCarving 对图像进行剪裁的结果，而右图则是经过 GrabCut 提升前景像素重要性（能量值）后图像剪裁的结果。第一幅图的人像发生了扭曲变形，双眼间距明显变小。而后者能够较为完整地保留图像中的人像，即“重要区域”，删除较多的部分则是图像左半部分的背景。

2. 加速剪裁过程

经过实验，SeamCarving 把一帧 500500 的图像剪裁到 500425 大小需要超过 2 分钟的时间，这样的时间性能还有很大的提升余地。在实验过程中发现，计算能量累积图 M 是占用时间较多的步骤之一，所以为了避免重复计算 M，本文试图根据单次 M 的计算结果删除多条连通路径。这个过程有两种简易的方式实现，下文是对两种方式的实现与探讨：

1.删除一条连通路径周围的像素在绝大多数情况下，连通路径周围的像素与路径上的像素较为相似，通常的能量值也较小。所以第一个思路即对连通路径进行“加粗”，从而一次删除多条路径，如下图所示：

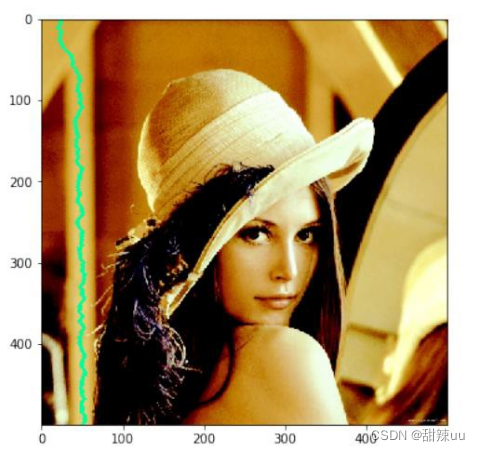
这种方式的弊端显而易见：如果仅删除一条较“窄”的路径，周围像素的色差不会很明显，而删除了较“粗”的路径，图像中容易出现可见色差。

2.利用 M 计算出多条路径其思路如下：根据 M 的计算结果，算法按照能量累积从小到大的顺序，贪心地寻找没有“交叉”的多条路径，结果如下图三条绿色路径所示：

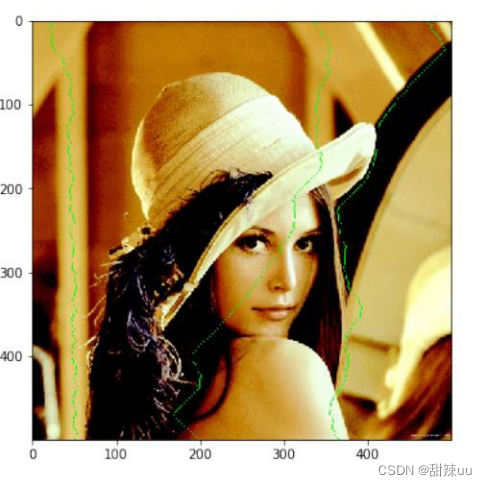
当然，这种方式的弊端也较为明显：为了使路径没有交叉的像素，靠后选择的路径能量累积值可能较大，那条路径很有可能是需要保留的路径。

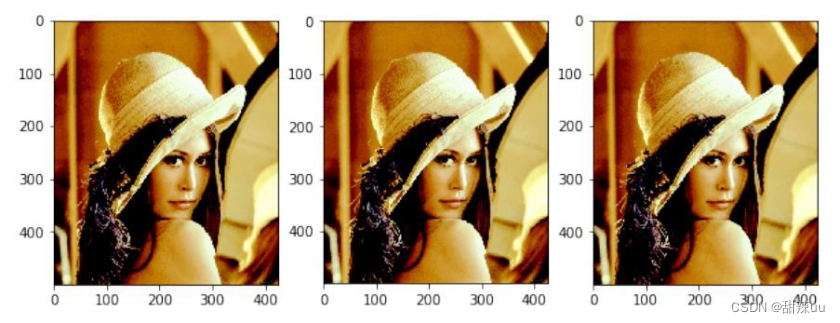
上图中分别使用三种方式将 500500 的图像剪裁至 500425 像素，三种剪裁方式分别是一次删除单一路径、上述方法一（“粗”路径）以及上述方法二（多条非交叉路径），其中方法一和方法二均一次删除三条路径用以加速算法。总体来说，三种方法的到的结果较为近似，但上述方法一由于删除的路径较“粗”，可以在人脸上看到明显的色差，效果不如其他两种方式。三种方式剪裁的时间分别为：

可以看出，两种改进方式较之原方法，时间性能均提升了 3 倍左右。然而综合来看，两种加速算法都有较大的弊端，而且尽管时间性能成倍提升，也远远不能达到实时运行，这很大程度上受限于动态规划时间复杂度限制，如果要彻底改进 SeamCarving 的时间性能，可能需要改变动态规划这一关键步骤。