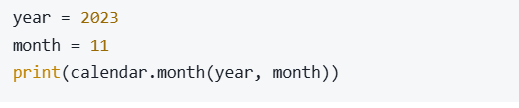
完全背包

感觉越写越糊涂了，初始化怎么做的？递推公式怎么来的？

• 状态变量
  
• 初始化 f[0][0] = 0
• 代码
  这里的 f[i][j] = f[i][j-w[i]]，就是和0-1背包最大的不同

for(int i=1; i<=n; i++) { //物品i
  for(int j=1; j<=m; j++) {
    if(j<w[i])  f[i][j] = f[i-1][j];
    else f[i][j] = max(f[i-1][j], f[i][j-w[i]] + c[i]);
  }
}

时间复杂度 O(n*m)
空间复杂度 O(n*m)

• 一维数组
  
  继续简化代码变为

for(int i=1; i<=n; i++) {
  for(int j=w[i]; j<=m; j++) { ---这里变动
    f[j] = max(f[j], f[j-w[i]] + c[i]);
  }
}

• 与01背包的区别
  

卡码52. 携带研究材料

https://kamacoder.com/problempage.php?pid=1052

import java.util.*;

public class Main {
    
    public static void main(String[] args) {
       Scanner sc = new Scanner(System.in);
       int N = sc.nextInt(); //研究材料的种类
       int bagSize = sc.nextInt(); //行李空间 
       
       int[] weight = new int[N];
       int[] value = new int[N];
       for(int i=0; i<N; i++) {
           weight[i] = sc.nextInt();
           value[i] = sc.nextInt();
       }
       
       int[]dp = new int[bagSize+1];
       for(int i=0; i<N; i++) {
           for(int j=weight[i]; j<bagSize+1; j++) {
               dp[j] = Math.max(dp[j], dp[j-weight[i]] + value[i]);
           }
       }
       System.out.println(dp[bagSize]);
    }
}

518. 零钱兑换 II

这道题使用动态规划：当前状态依靠上一状态得到。

• 初始化出错：dp[0]=1的意思是，amount等于0的时候 凑成总金额0的货币组合数为1

class Solution {
    public int change(int amount, int[] coins) {
        int[]dp = new int[amount+1];
        dp[0] = 1;
        //dp[j]: 总金额为j的时候，有dp[j]种方式找零钱
        //
        int M = coins.length;
        for(int i=0; i<M; i++) {
            for(int j=coins[i]; j<= amount; j++) {
                dp[j] = dp[j] += dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
}

• 别人的二维数组解法

class Solution {
    public int change(int amount, int[] coins) {
        int n = coins.length;
        int[][] f = new int[n + 1][amount + 1];
        f[0][0] = 1;
        for (int i = 0; i < n; i++) {
            for (int c = 0; c <= amount; c++) {
                if (c < coins[i]) {
                    f[i + 1][c] = f[i][c];
                } else {
                    f[i + 1][c] = f[i][c] + f[i + 1][c - coins[i]];
                }
            }
        }
        return f[n][amount];
    }
}

377. 组合总和 Ⅳ

和518. 零钱兑换 II 的区别：① 求组合(518)先物品后背包 ② 求排列(377)先背包后物品

先物品后背包：先把物品0放进来，然后把物品1放进来，所以我们计算的情况顺序只有（物品0，物品1）的情况，不会出现（物品1，物品0），因此为组合

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[]dp = new int[target+1];

        //初始化
        dp[0] = 1;

        //递推
        //dp[i][j]表示 从物品0-i任取，满足恰好等于 j ,所有可能的组合有dp[i][j]个
        for(int i=0; i<=target; i++) {
            for(int j=0; j<nums.length; j++){
                if (i >= nums[j]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }

        return dp[target];
    }
}

// 完全背包的初始化不太一样
// 0-1背包对首行（当weight[0]<=j的时候，dp[0][j]=value[i]）首列进行初始化

70. 爬楼梯 （进阶）

• 错误：for i=1 for j=1
• 而且 j<=M ，包含等于

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int bagSize = sc.nextInt();
        int M = sc.nextInt();
        int[] dp = new int [bagSize+1];
        
        dp[0] = 1;
        
        for(int i=1; i<bagSize+1; i++) {
            for(int j=1; j<=M; j++) { //物品
                if(i >= j) {
                    dp[i] += dp[i-j]; 
                }
            }
        }
        System.out.println(dp[bagSize]);
    }
}