1. 两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

解析

使用 Hash 表记录所有已遍历元素及对应的下标，遍历的同时查找满足条件的数字是否已遍历，若找到返回即可。

代码

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer,Integer> map = new HashMap<>();
        int[] res = new int[0];
        for(int i = 0; i < nums.length; i++){
            if(map.containsKey(target - nums[i])) return new int[]{i, map.get(target - nums[i])};
            map.put(nums[i],i);
        }
        return res;
    }
}

2. 两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

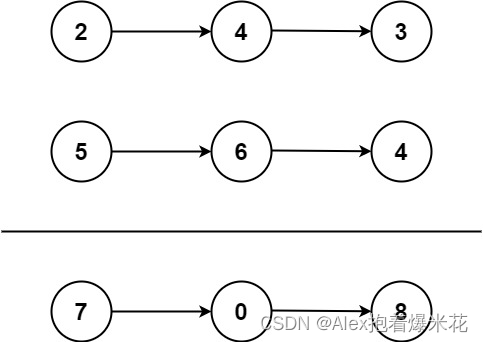
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

解析

按位模拟加法，注意循环条件不要忘记进位。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        int cur = 0;
        int carry = 0;//进位
        ListNode dummy = new ListNode();
        ListNode helper = dummy;
        while(l1 != null || l2 != null || carry != 0){
            int v1 = l1 == null ? 0 : l1.val;
            int v2 = l2 == null ? 0 : l2.val;
            int sum = v1 + v2 + carry;
            cur = sum % 10;
            carry = sum / 10;
            helper.next = new ListNode(cur);
            helper = helper.next;
            if(l1 != null) l1 = l1.next;
            if(l2 != null) l2 = l2.next;
        }

        return dummy.next;
    }
}

3. 无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

解析

使用一个数组记录每个字符出现次数，在遍历的同时移动窗口左边界，最后返回窗口长度的最大值即可。
注：子串是连续的，子序列是不连续的

代码

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int[] map = new int[128];
        int res = 0;
        // i ： 窗口右边界 j : 窗口左边界
        for(int i = 0 , j = 0;i < s.length(); i++){
            map[s.charAt(i)]++;
            while(map[s.charAt(i)] > 1){ //重复
                map[s.charAt(j++)]--;//窗口左移
            }
            res = Math.max(res, i - j + 1);// i - j + 1是窗口的长度
        }

        return res;
    }
}

4. 寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2
示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

解析

本题可以抽象为：给定两个数组 A、B，如何找到从小到大排列的第 K 个数字，而中位数存在 K = K -1的下标映射关系

代码

class Solution {
  public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n = nums1.length + nums2.length;
        if(n % 2 == 0){
            return (findKth(nums1, 0, nums2, 0, n / 2) + findKth(nums1, 0, nums2, 0, n / 2 + 1)) / 2.0;
        }else{
            return findKth(nums1, 0, nums2, 0, n / 2 + 1);
        }
        
    }
    //i: nums1的起始位置 j: nums2的起始位置
    public int findKth(int[] nums1, int i, int[] nums2, int j, int k){
        if( i >= nums1.length) return nums2[j + k - 1];//nums1为空数组
        if( j >= nums2.length) return nums1[i + k - 1];//nums2为空数组
        if(k == 1){
            return Math.min(nums1[i], nums2[j]);
        }
        int midVal1 = (i + k / 2 - 1 < nums1.length) ? nums1[i + k / 2 - 1] : Integer.MAX_VALUE;
        int midVal2 = (j + k / 2 - 1 < nums2.length) ? nums2[j + k / 2 - 1] : Integer.MAX_VALUE;
        if(midVal1 < midVal2){
            return findKth(nums1, i + k / 2, nums2, j , k - k / 2);
        }else{
            return findKth(nums1, i, nums2, j + k / 2 , k - k / 2);
        }        
    }
}