先直接上连接
941有效的山脉数组
845数组中的最长山脉
2100适合打劫银行的日子.
2420找到所有好下标.
什么是两个维度?
这里是从代码随想录里面学习到的思考方式,开门见山地说,就是两个方面去考虑题目,比如,要求第i位的元素,左边元素都得非递增,右边元素都得非递减,那同时考虑这两个维度来做题的话会难一些,这个时候可以先考虑一个维度,再去考虑另外一个维度来做题,即我们先考虑有i左边有多少个非递增的,遍历完一次之后再回来看i右边有多少个非递减的
今天的题目主要以动态规划为主,这里就不多废话了,直接对题目进行分析吧
941有效的山脉数组
这道题是用作举例一下什么叫两个维度,其实不需要用到dp,双指针即可
,先考虑一个维度,左边元素比当前元素小,即左山腰,找到山峰,然后再去找右山腰
附上代码
public static boolean validMountainArray(int[] arr) {
//山脉数组,从两边找即可
// 双指针
int left = 0;
int right = arr.length - 1;
// 注意防止指针越界
while (left + 1 < arr.length && arr[left] < arr[left + 1]) {
left++;
}
// 注意防止指针越界
while (right > 0 && arr[right] < arr[right - 1]) {
right--;
}
// 如果left或者right都在起始位置,说明不是山峰
if (left == right && left != 0 && right != arr.length - 1) {
return true;
}
return false;
}845数组中的最长山脉
这道题就是两个维度的动态规划,当然双指针也能做
运用到的就是上面所说的两个维度的思考,可以发现,对某一个山脉的时候,我们如果上来就直接把两个维度都思考进去,是比较难做题的,这个时候不妨先考虑其一,我们先找以当前位作为山峰,先去找左山腰,遍历完之后得到一个只求当前位左边是非递减的dp,再另起一个记录右山脉的dp数组,最后将两个都合并起来去得到本题的解法。
//动态规划做法
//能否成为山脉数组的条件:长度至少为3,即有必须有两个山腰(往两边递减)
//子数组默认连续,子序列不一定
//可以思考出本题其实有两个维度,一个是找到递增一个是找到递减
//共同点是,以某个点作为顶点往两边扩散
//因此建立两个dp数组,从左到右和从右到左
//对原数组进行分析有三种情况:从头到尾递增,从头到尾递减,有增有减
//有增有减的情况就决定了某个点一定能作为山顶点
//因此我们最后求结果的时候只需要比对以i作为山顶的时候,left[i]和right[i]的值即可
public int longestMountain1(int[] arr) {
int len = arr.length;
if(len<=2) return 0;
//dp[i]:以i作为山顶,左向顶/右向顶递增的最长子数组为dp[i]
int left[] = new int[len];
int right[] = new int[len];
//初始化---每个点都可以作为山顶
Arrays.fill(left, 1);
Arrays.fill(right, 1);
//遍历顺序
//左向顶的最长
//最左边的一定无法成为山脉数组,因为没有左山腰
for(int i = 1;i<len-1;i++) {
if(arr[i]>arr[i-1]) {
left[i] = left[i-1]+1;
}
}
//最右边的一定无法成为山脉数组,因为没有右山腰
for(int i = len-2;i>=0;i--) {
if(arr[i]>arr[i+1]) {
right[i] = right[i+1]+1;
}
}
//长度至少为3才能算山脉数组,因此需要都大于1
int res = 0;
//枚举每个点(除了最左和最右)作为山顶来求最长山脉数组
for(int i = 1;i<len-1;i++) {
if(left[i]>1&&right[i]>1) {
//重复计算山顶,因此-1
res = Math.max(res, left[i]+right[i]-1);
}
}
return res;
}当然也附上双指针做法
//非动态规划做法:找到某一个极大值,然后找的过程中左边一定是递增的,那么去检索右边
public int longestMountain(int[] arr) {
int n=arr.length,ans=0;
for(int i=1;i<n-1;i++){
if(arr[i]>arr[i-1]&arr[i]>arr[i+1]){
int l=i-1,r=i+1;
while(l>=0&&arr[l]<arr[l+1]){l--;}
while(r<n&&arr[r]<arr[r-1]){r++;}
ans=Math.max(ans,r-l-1);
}
}
return ans;
}2420找到所有好下标.
2100适合打劫银行的日子.
这两道题就放一起了,因为基本上是一样的,不同之处在于2100包含本位的,2420不包含本位
什么意思呢?
首先看一下2100的题目

看一下2100执行结果
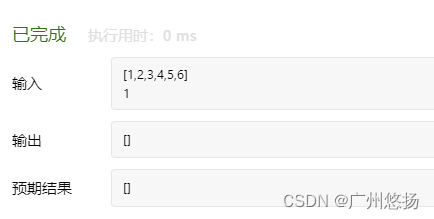
再来看一下2420的题目
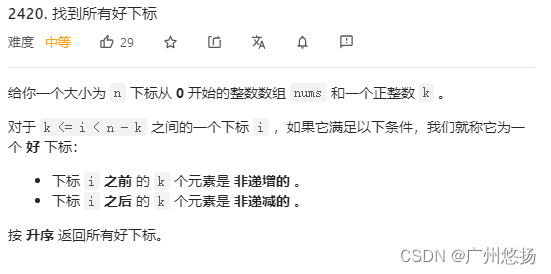
2420的执行结果

可以发现,两者题目描述上唯一的差别就是,2420是讨论i的前后,即不包含本位
2100虽然也是讨论i的前后,但是很明显可以看出这个前后其实是包含i的,对比一下两个预期结果就可以看得出来,2420中可以构成[1,2,3],只有不包含本位的时候才成立,单个数字既是非递增也是非递减,而2100预期结果是[],很显然这里只有包含了本位,即照题目的意思是[1,2]和[2,3],这里只有非递减,这点我也是想了很久,去找了大佬们的解释,还有通过预期结果确定的
那么在代码实现上也会有不同
附上2100的代码
//2100
public static List<Integer> goodDaysToRobBank(int[] se, int time) {
int n = se.length;
List<Integer> list = new LinkedList<>();
//要求前后有k个元素,最后返回下标,可以发现 这个题其实就是子数组
//dp[i]:以i下标结尾的数组中,构成i(前/后)非递(增/减)的子数组的长度为dp[i]
int[]left = new int[n+2];
int[]right = new int[n+2];
for(int i = 1;i<n;i++) {
if(se[i]<=se[i-1]) {
left[i+1] = left[i] + 1;
}
}
for(int j = n-2;j>=0;j--) {
if(se[j+1]>=se[j]) {
right[j+1] = right[j+2] + 1;
}
}
//统计当前位前后是否满足条件,包含本位
for(int i = 1;i<=n;i++) {
if(left[i]>=time && right[i]>=time) {
list.add(i-1);
}
}
return list;
}附上2420的代码
public static List<Integer> goodIndices(int[] nums, int k) {
int n = nums.length;
List<Integer> list = new LinkedList<>();
//要求前后有k个元素,最后返回下标,可以发现 这个题其实就是子数组
//dp[i]:以i下标结尾的数组中,构成i(前/后)非递(增/减)的子数组的长度为dp[i]
int[]left = new int[n];
int[]right = new int[n];
//初始化---每个数都置为一,否则无法应对123,k=1这种情况
//i本身就满足与i构成非递减非递增的关系
//(123满足2前1位非递增,后一位非递减)
Arrays.fill(left, 1);
Arrays.fill(right, 1);
for(int i = 1;i<n;i++) {
if(nums[i]<=nums[i-1]) {
left[i] = left[i-1] + 1;
}
}
for(int j = n-2;j>=0;j--) {
if(nums[j+1]>=nums[j]) {
right[j] = right[j+1] + 1;
}
}
//统计当前位前后是否满足条件,不包含本位
for(int i = 1;i<n-k;i++) {
if(left[i-1]>=k && right[i+1]>=k) {
list.add(i);
}
}
return list;
}