MoCo方法由何凯明团队提出,是无监督对比学习的代表作。经过MoCo预训练的视觉表征迁移到各种下游任务时,其效果超过了有监督预训练模型。
两点创新
对比学习的思想是将相似的样本距离拉近,不相似的样本距离拉远。对比学习主要在两方面进行设计:
- 代理任务
- 损失函数
MoCo将对比学习当作字典查询任务,在字典中与query匹配的key视为正样本,否则为负样本:
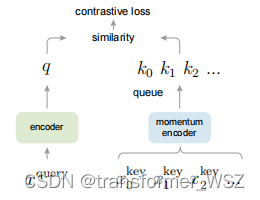
损失函数InfoNCE为:
L
q
=
−
log
exp
(
q
⋅
k
+
/
τ
)
∑
i
=
0
K
exp
(
q
⋅
k
i
/
τ
)
\mathcal{L}_q=-\log \frac{\exp \left(q \cdot k_{+} / \tau\right)}{\sum_{i=0}^K \exp \left(q \cdot k_i / \tau\right)}
Lq=−log∑i=0Kexp(q⋅ki/τ)exp(q⋅k+/τ)
其中,
τ
\tau
τ 是温度系数,该超参设置需要注意。太大会导致query与所有样本的相似度都很接近,太小会导致模型偏向学习区分度高的样本。
上式与多分类交叉熵损失函数非常相似,只不过前者 K K K 表示样本类别,而后者表示正样本与负样本的总个数。
与传统自监督学习对比
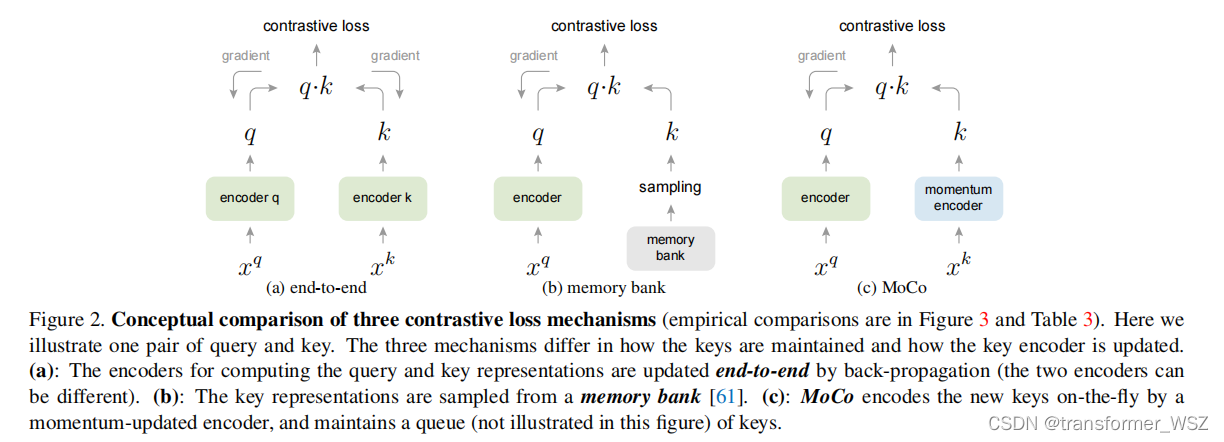
- 图(a)中两个编码器同步更新,保证了样本特征的一致性,但负样本个数受限,即使能达到8000多,还是无法放下所有的负样本
- 图(b)放下了所有的负样本,但bank中不同样本的特征是在不同时刻的编码器下获得的,牺牲了特征的一致性
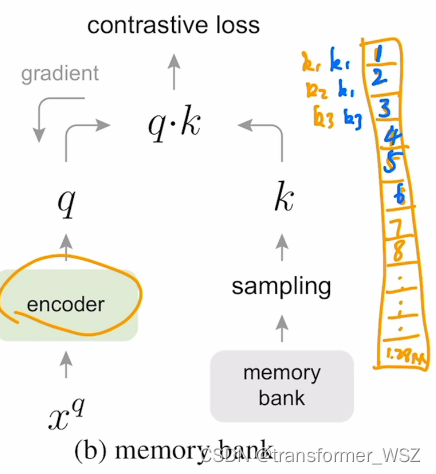
- 图©则是采样了动量更新key编码器的方式,解决了字典大小受限和特征不一致性问题:
θ k ← m θ k + ( 1 − m ) θ q \theta_{\mathrm{k}} \leftarrow m \theta_{\mathrm{k}}+(1-m) \theta_{\mathrm{q}} θk←mθk+(1−m)θq
伪代码解读

-
新的batch进行一轮前向传播
-
更新query编码器参数
-
动量更新key编码器参数
-
将该batch放入队列
- 虽然同一队列的batch样本表征仍然是不同时刻的key编码器获得,但由于key编码器更新非常缓慢,样本表征的差异可以忽略不计:

- 虽然同一队列的batch样本表征仍然是不同时刻的key编码器获得,但由于key编码器更新非常缓慢,样本表征的差异可以忽略不计:
-
将老batch移出队列:这样MoCo就能无限扩展,预训练海量样本
实验结果
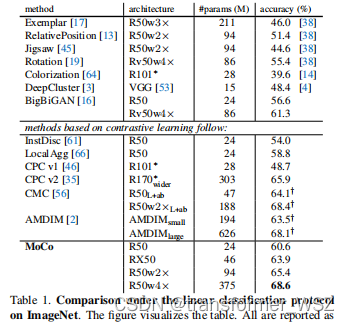
原始数据集ImageNet
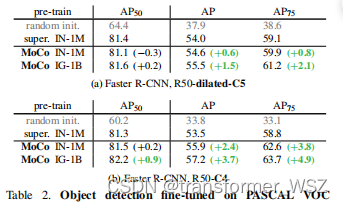
下游任务
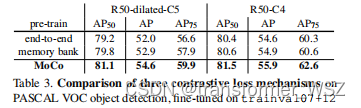
与传统自监督学习对比
参考
- MoCo 论文逐段精读【论文精读】
- 大概是全网最详细的何恺明团队顶作 MoCo 系列解读!(上)