以RGB图像为例。
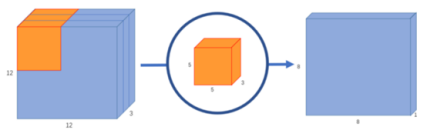
        一个12*12的像素图，对其进行5*5的卷积，最后得到一个8*8【计算过程：(12-5)/1+1=8】的像素图。

        RGB图像有3个通道（12*12*3），所以卷积核也要有3个通道（5*5*3），对像素图进行卷积后得到的结果是8*8*1而不是8*8*3的图像。最后像素图的深度（输出图像的信道数）取决于卷积核的个数。

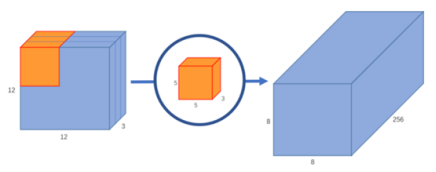
        如果要得到8*8*256的结果，应该这样做：用256个5*5*3的卷积核来卷12*12*3的像素图。最后得到的结果进行堆叠就是8*8*256的图像。（256个5*5*3的卷积核可以想象成它的输入信道数为3，而输出信道数为256，两者互不影响。）

        注：通道数就是使用的卷积核的个数。就像上面解释的一样，假如输入的图是RGB3通道的，如果我们只卷积一次，就只会输出一个值，由于输入图片是 3 通道的，输出通道反而减少了，为了保留特征，会进行多次卷积操作，比如进行 256 次卷积操作就可以得到一个 256 通道的输出了，然后输出的通道数就叫做feature map。

        附卷积、池化操作的计算公式：

假设输入维度为 H1×W1×C1，输出为 H2×W2×C2，则有

        H2 = （H1-F+2P）/ S+1

        W2 = （W1-F+2P）/ S+1

        C2 = k

        这里 F：filter大小；P：边界填充，为0或1；S：步长；k：filter个数。

参考文章：卷积过程中关于通道数的问题_赵 XiaoQin的博客-CSDN博客_卷积通道数