一、前言

大家好久不见，今天我们一起来学习一道很经典、也很有难度的一道题目——N皇后

二、题目信息

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间 不能 相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

说白了，这道题题目就是让所有皇后之间不在同一行、同一列、同一对角线，求出所有满足此要求的棋盘！

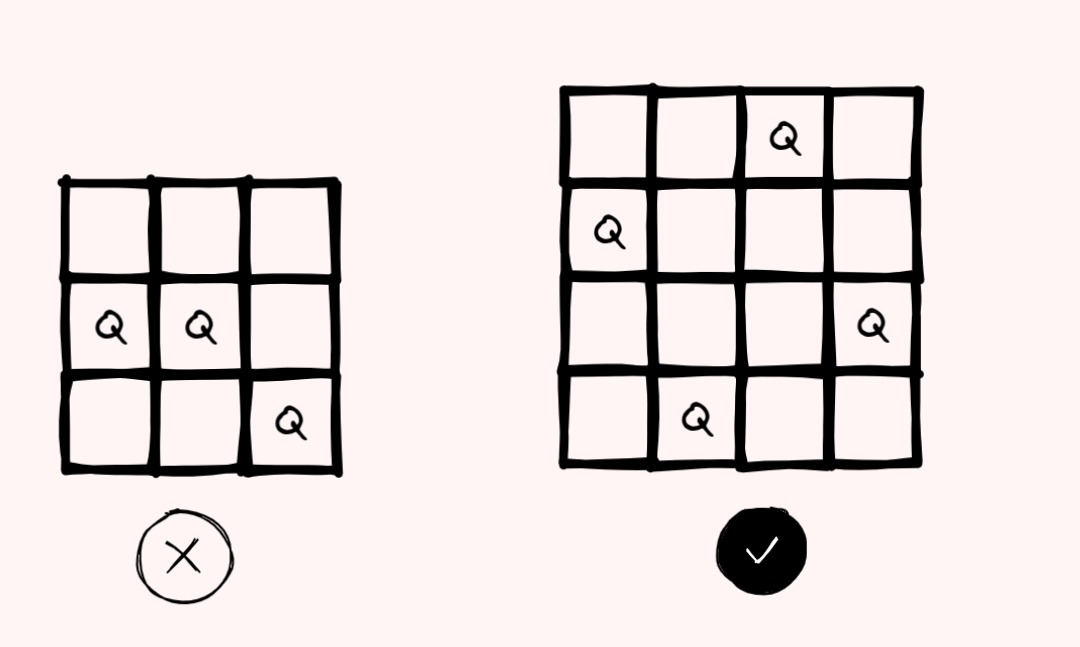
在这里插入图片描述

如图示，左边3X3的样例就是不符合要求的！！！我们要收集 所有 像4X4这样的样例！！！

三、解题思路

思路分析

一看到这道题目，我们会很自然想要用暴力算法来解决，例如设置一个for循环来遍历第一行、再来一个for循环遍历第二行…依此类推。

暴力算法当然是可以解决这道题目的，但这里就会有一个问题，3X3的棋盘我们套3个循环，那4X4的棋盘呢？5X5的又怎么办呢？

因此我们用暴力循环其实是不太适合这道题目的，因为我们没法控制每次套几个循环，那有没有一种方式能够让我们控制有几个for循环呢？

答案是有的！！！看过上次讲解的小伙伴应该知道，回溯算法恰好是用来实现多重for循环的一个算法，他本质上也是一个暴力算法，回溯算法基础。

我们按照暴力算法的思路先来分析一下：

核心思路就是：定住第一行的一个元素，然后去下一行定住一个元素，再去下一行定住一个元素，直到底行。

画图表示：
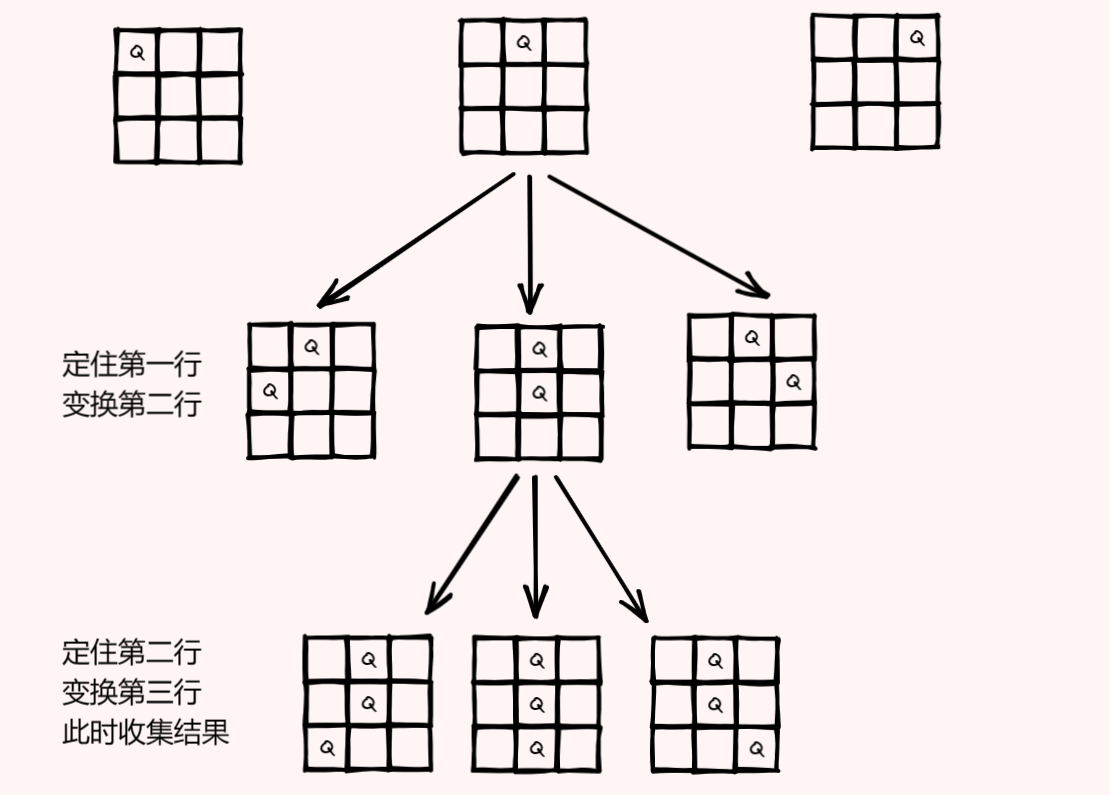
在这里插入图片描述

因为图片大小原因，我只把中间过程的某一步完全画了出来，大家明白暴力算法的思路即可。

那么怎么实现我们这个 可变for循环 呢，是的，就是使用 回溯算法 ！

之前说过，回溯算法本质也是暴力算法，他通过递归的方式来实现多重for循环，从而解决暴力算法无法设计多重循环的问题，那按照回溯算法的基本思路，我们一起来设计一下！！

✔️递归终止条件

什么时候棋盘放下了所有皇后，什么时候就停止递归，啥时候所有皇后都放下了？当然是最后一层for循环也走完了的时候。

这里我再简单补充一句：为什么是for循环走完才证明皇后全都放下了？之前放完皇后不行吗

不要忘记规则的约束，同一行或同一列或同一斜线上的皇后会相互攻击，如果你把两个皇后放到同一行，直接就不符合规则了，因此一行放且必须放一个！！！

✔️每一层的处理逻辑

如果不在最终层，我们就要用递归的思路去实现多重for循环！

for(int i=0;i<n;i++)
{
	chessboard[row][rol] = 'Q'; //确定好这一层的一个皇后
	backtracking();//递归此函数，继续向下执行相同逻辑
	chessboard[row][rol] = '.'; //将刚刚确定好的皇后剔除，换成下一个
	
}

固定好一个元素，要去递归执行下一层了，当满足收集结果的条件后，递归结束，再将棋盘上的皇后剔除，固定下一个元素继续执行相同的逻辑。

能够跳回原来的状态，这就是回溯算法的精髓。

✔️收集结果

当我们进入最终层，就要准备收集结果了，并非所有棋盘都需要收集，我们只需要收集满足 皇后同一行或同一列或同一斜线上 的棋盘，因此我们需要判断棋盘是否符合要求！

但要把所有情况都算出再来检查就会产生大量时间浪费和代码冗余，因此我们采用放皇后时，就检查棋盘是否符合要求，如果不符合，直接进行下一次循环！

要检查当前位置可不可以放置皇后，需要满足三个条件
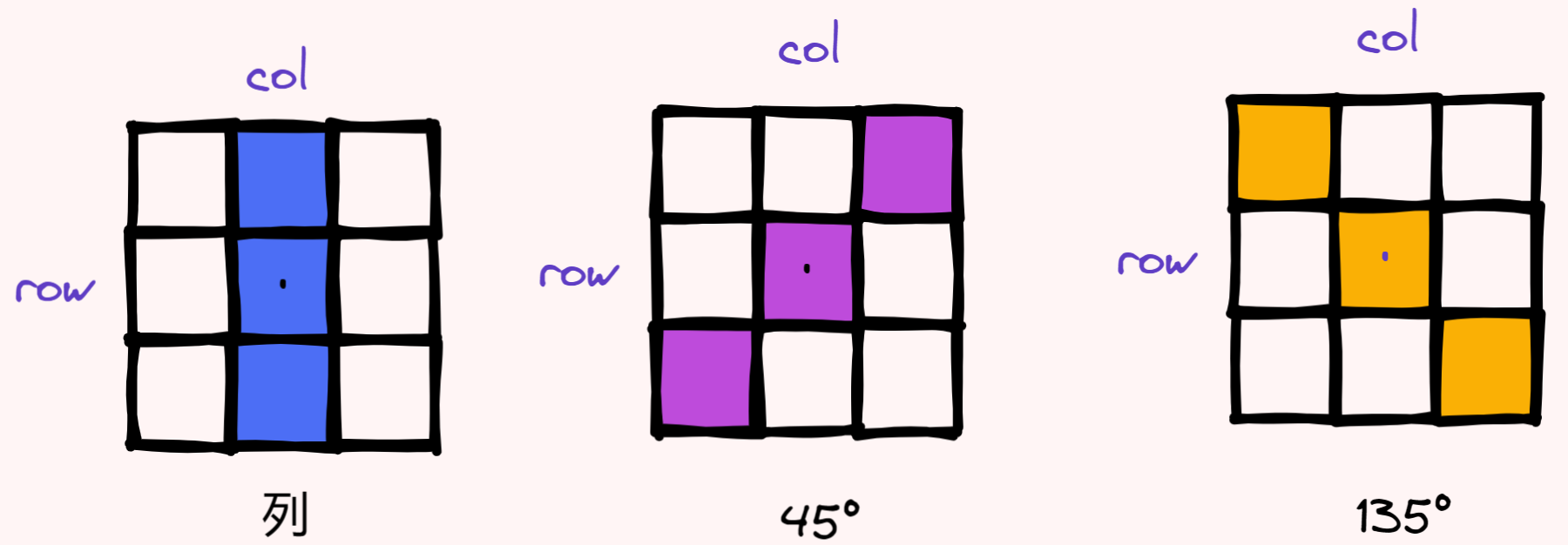
在这里插入图片描述

针对以上三种情况，我们写一个简单函数：
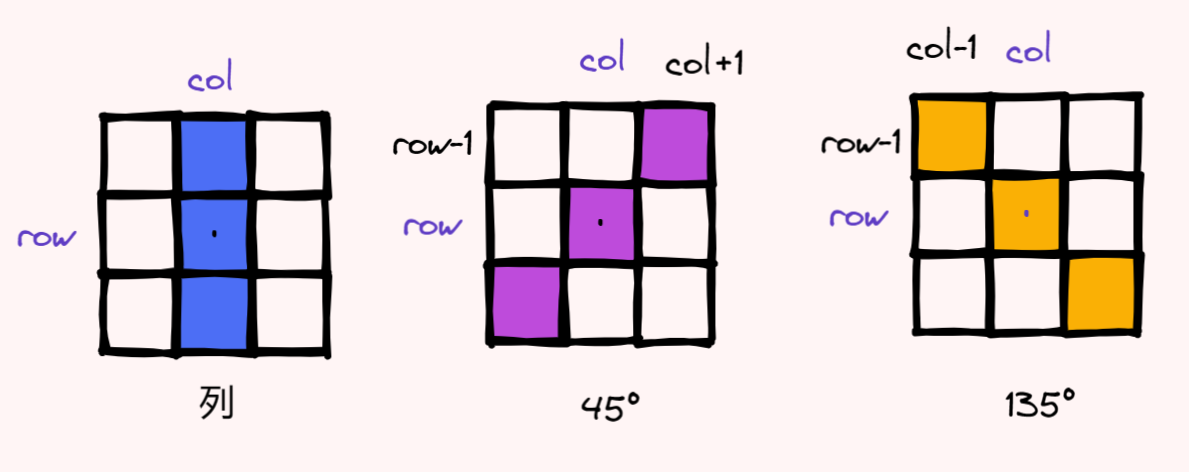
在这里插入图片描述

bool CheckBoard(vector<string>& chessboard,int row,int col,int n)
{
	//此函数判断第row行第rol列能不能放皇后

	//同一列
	for (int i = 0;i<row;i++)
	{
		if (chessboard[i][col] == 'Q')
		{
			return false;
		}
	}

	//45°
	for (int i = row - 1, j = col + 1; i >= 0 && j < n ;i--,j++)
	{
		if (chessboard[i][j] == 'Q')
		{
			return false;
		}
	}

	//135°
	for (int i = row-1,j = col-1;i>=0 && j>=0;i--,j--)
	{
		if (chessboard[i][j] == 'Q')
		{
			return false;
		}
	}

	return true;

}

四、参考代码

class Solution {
public:
    vector<vector<string>> result;
    void backtracking(int n, int row, vector<string>& chessboard) 
    {
        if (row == n) 
        {
            result.push_back(chessboard);
            //收集合法的结果，只有合法才能来到最后！！！
            return;
        }
        for (int col = 0; col < n; col++) //行固定了，列开始回溯！！
        {
            if (CheckBoard(chessboard,row, col, n)) 
            { 
                // 验证合法就可以放
                chessboard[row][col] = 'Q'; // 放置
                backtracking(n, row + 1, chessboard);//去遍历下一层！！
                chessboard[row][col] = '.'; // 撤销
            }
        }
    }
    bool CheckBoard(vector<string>& chessboard,int row,int col,int n)
    {
        //此函数判断第row行第rol列能不能放皇后

        //同一列
        for (int i = 0;i<row;i++)
        {
            if (chessboard[i][col] == 'Q')
            {
                return false;
            }
        }

        //45°
        for (int i = row - 1, j = col + 1; i >= 0 && j < n ;i--,j++)
        {
            if (chessboard[i][j] == 'Q')
            {
                return false;
            }
        }

        //135°
        for (int i = row-1,j = col-1;i>=0 && j>=0;i--,j--)
        {
            if (chessboard[i][j] == 'Q')
            {
                return false;
            }
        }

        return true;
    }
    vector<vector<string>> solveNQueens(int n) 
    {
        vector<string> chessboard(n, string(n, '.'));
        backtracking(n, 0, chessboard);
        return result;
    }
};