一、问题

二、分析

这道题是一个在数上做分组背包问题的模型，那么为什么是分组背包呢？作者在之前的文章中进行过详细地讲解，转移方程，初末状态的设置等等，都在AcWing 10. 有依赖的背包问题（分组背包问题 + 树形DP）中有过超级详细地解释。

这道题唯一不同的就是，之前是把点当作物品，这道题是把边当作物品，那么其实也没有什么区别，但细节处还要做一些处理。

我们看下面的分析：

首先这道题我们要是当作背包问题的话，物品体积就是1，价值就是边上的苹果数目。

同时这道题要求的是最后选出的边得是和根节点root连通的。

这就说明，我们只有选了和父节点连接的边，才能选择这个父节点下面的和子节点连接的边。

1、状态表示

$f[u][i][j]$表示在以$u$为根节点的树上剪树枝，在与$u$相连的前$i$个子树中挑选并保留$j$根树枝，所能保留的最大苹果数目。

2、状态转移

由于是背包模型，所以我们面对的是第$i$棵子树中的树枝选还是不选，如果选的话，怎么选？

我们还是子树看作一个物品组，然后按照体积（树枝的数量）作为组内物品分类的标准进行分类。
这样做的具体方式可以看作者刚才提到的文章：AcWing 10. 有依赖的背包问题（分组背包问题 + 树形DP）

这里有一个细节需要注意：

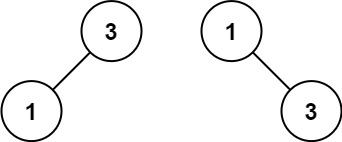
我们看下面的图：

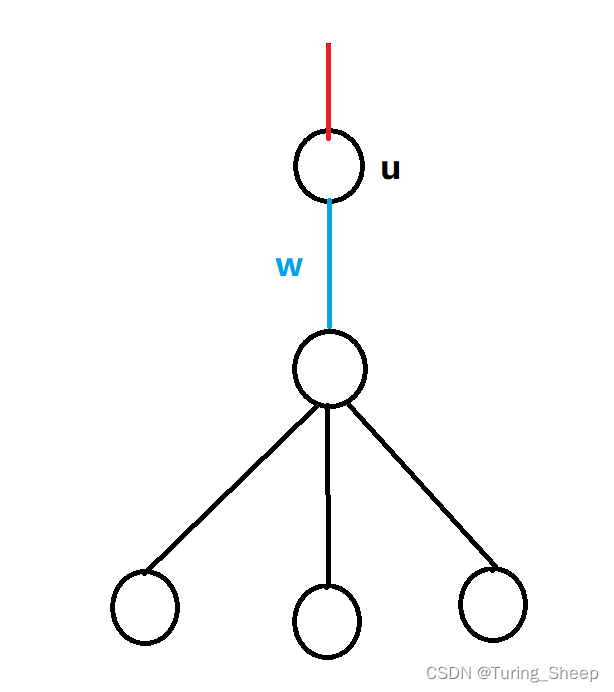
我们首先需要留出一条边，这条边是红线，同时，我们还要额外加上一条蓝线，这条蓝线连接的是u和子树。因为子树中不包括w，所以我们需要自己额外加上w。这个w我们算下面方程的在k里，因此这个k就分成了两部分，k - 1是子树中的，还有一条就是蓝线w。

$$f[u][i][j]=max(f[son][nums][k]+f[u][i-1][j-k-1]+w,f[u][i][j])$$
这个k的范围是$0$到$j-1$的，因为我们选择了子树中的树枝就需要将父节点相连的那个树枝选上。所以我们要留出1根树枝的位置。

3、循环设计

显示DFS遍历子树，然后枚举体积，再写转移方程。

三、代码

这里写的是空间优化后的代码。

#include<bits/stdc++.h>
using namespace std;
const int N = 110, M = 2 * N;
int h[N], e[M], ne[M], w[M], idx;

int f[N][M];

int n, m;

void add(int a, int b, int c)
{
	e[idx] = b, ne[idx] = h[a], w[idx] = c;
	h[a] = idx ++ ;
}

void dfs(int u, int father)
{
	for(int i = h[u]; i != -1; i = ne[i])
	{
		int son = e[i];
		if(son == father)continue;
		dfs(son, u);
		for(int j = m; j >= 0; j -- )
		{
			for(int k = 0; k <= j - 1; k ++ )
			{
				f[u][j] = max(f[son][k] + f[u][j - k - 1] + w[i], f[u][j]);
			}
		}
	}
}

int main()
{
	memset(h, -1, sizeof h);
	cin >> n >> m;
	for(int i = 0; i < n - 1; i ++ )
	{
		int a, b, c;
		cin >> a >> b >> c;
		add(a, b, c), add(b, a, c);
	}
	dfs(1, -1);
	cout << f[1][m] << endl;
	return 0;
}