Radiometry 辐射度量学

• 如何描述光照，定义了一系列的方法和单位
• 准确度量光的空间属性：
  • Radiant flux
  • intensity
  • irradiance
  • radiance
• 以物理正确的方式进行光照计算

Radiant Energy and Flux (Power)

Radiant Energy 定义

Radiant Energy 是电磁辐射的能量。单位为“焦耳”，符号为Q。

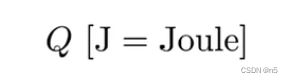
Radiant flux (power)定义

Radiant flux (power)是单位时间内辐射、反射、传输或接受的能量。其实就是功率，单位为瓦特(Watt) W。在光学中，一般使用单位流明(lumen) lm。注意，流明不等于瓦特：

所谓的流明（LM）简单来说，就是指蜡烛一烛光在一公尺（1 公尺 = 1 米）以外的所显现出的亮度。一个普通40瓦的白炽灯泡，其发光效率大约是每瓦10流明，因此可以发出400流明的光。流明表示的并不是flux（即辐射通量），而表示的是光通量（也叫明亮度）。流明和瓦特有着一定的对应关系（或称光功当量），经实验测定：当光波长为5550埃时，1瓦特相当于683流明，当光波长为6000埃时，1瓦特相当于391流明。 由此可见，同样发出1流明的光通量，波长为6000埃光所需的辐射通量约为波长为5550埃光的1.75倍左右。

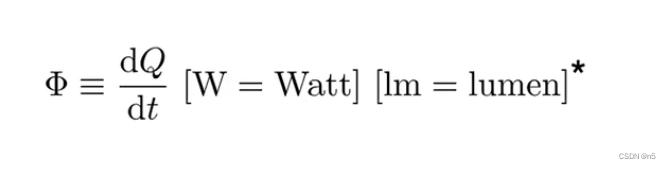
因为能量是和时间相关的，在辐射度量学中，考虑的都是单位时间的性质，因此定义flux，描述一个光源有多么亮。

从光子的角度定义Flux

Flux是在单位时间内，通过传感器的光子数量。

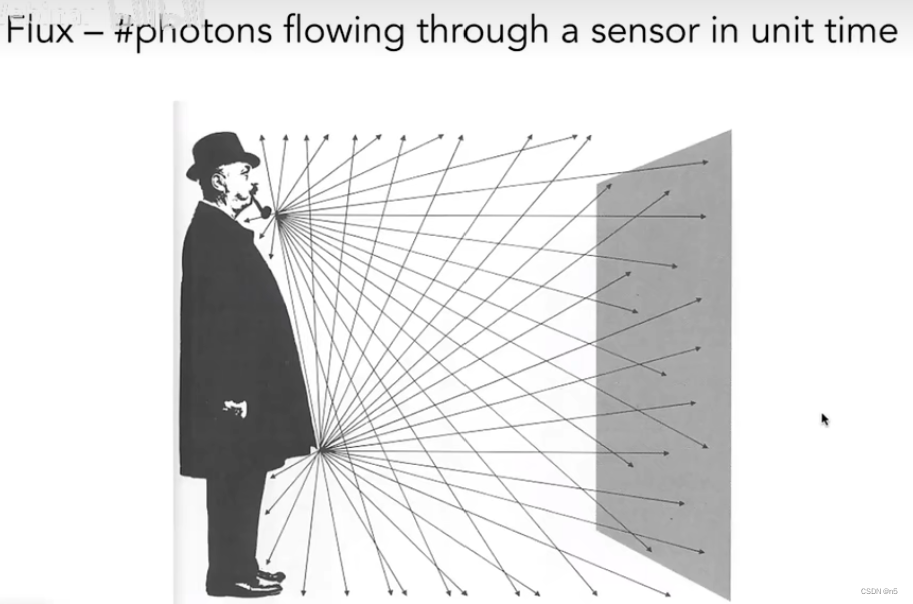
一个灯泡看上去更亮，是因为它单位时间内辐射出更多的光子。

描述光照的重要的物理量

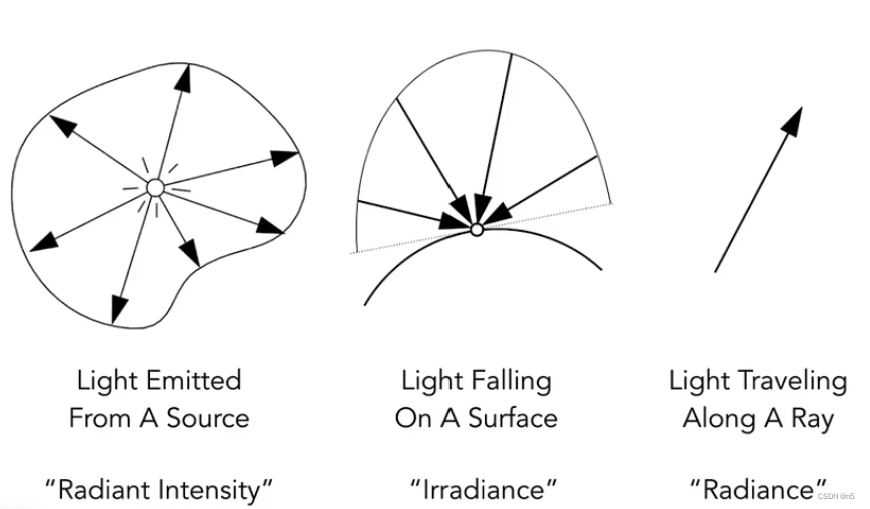
Radiant Intensity

定义：Radiant intensity是一个点光源辐射出的单位立体角的Power。（power per unit solid angle）

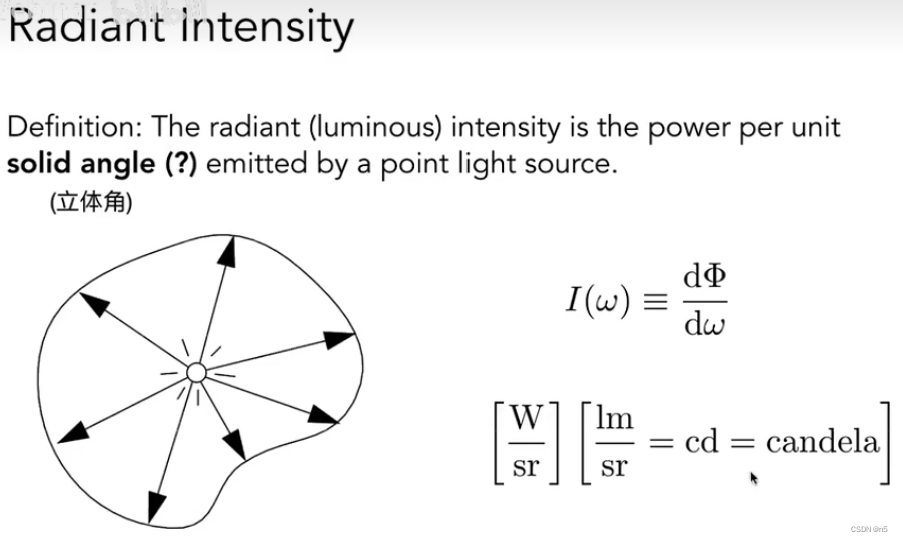
intensity的单位为 candela (cd)，这是标准单位制SI中的7个单位之一。

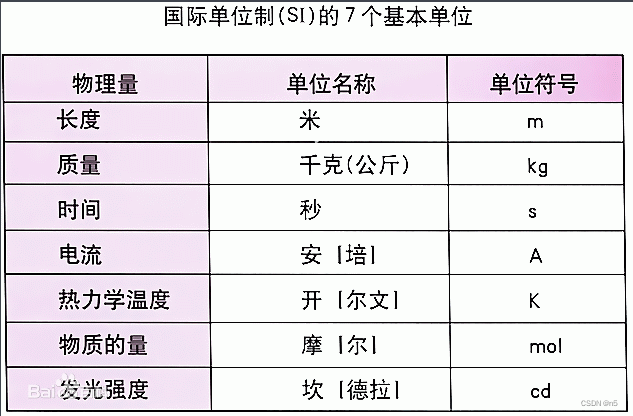
角度和立体角 (Angles and Solid Angles)

• 角度 = 弧长/半径，单位为弧度(radian)
  圆对应的角度是2$\pi$ radians。
  
• 立体角 = 对应球面面积/半径平方，单位为 steradian
  球的立体角是4$\pi$ steradians。
  

单位立体角（微分立体角） (Differential Solid Angles)

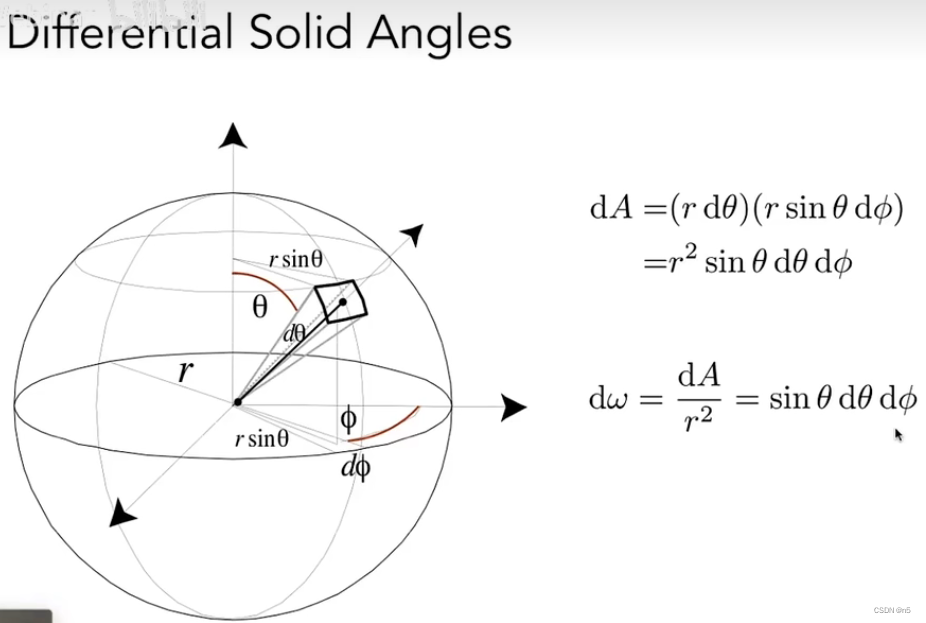
通过$\theta$和$\varphi$可以定义球面上的一个方向，当从该方向进行微小的变化d$\theta$,d$\varphi$时，计算微小的变化d$\theta$,d$\varphi$在球面上对应的微小的面积dA。dA除以半径r的平方得到的就是方向($\theta$,$\varphi$)对应的单位立体角d$\omega$。

对于整个球来说，将它所有方向的微分立体角进行积分，得到的立体角就是4$\Pi$。

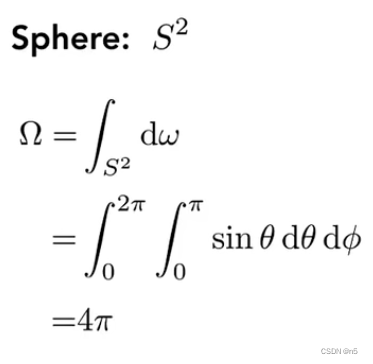
（注意这儿积分的范围，$\theta$的范围是[0,$\pi$], $\varphi$的范围是[0,$2\pi$]）

使用 $\omega$ 表示球面上的方向

$\omega$ = ($\theta$,$\varphi$)

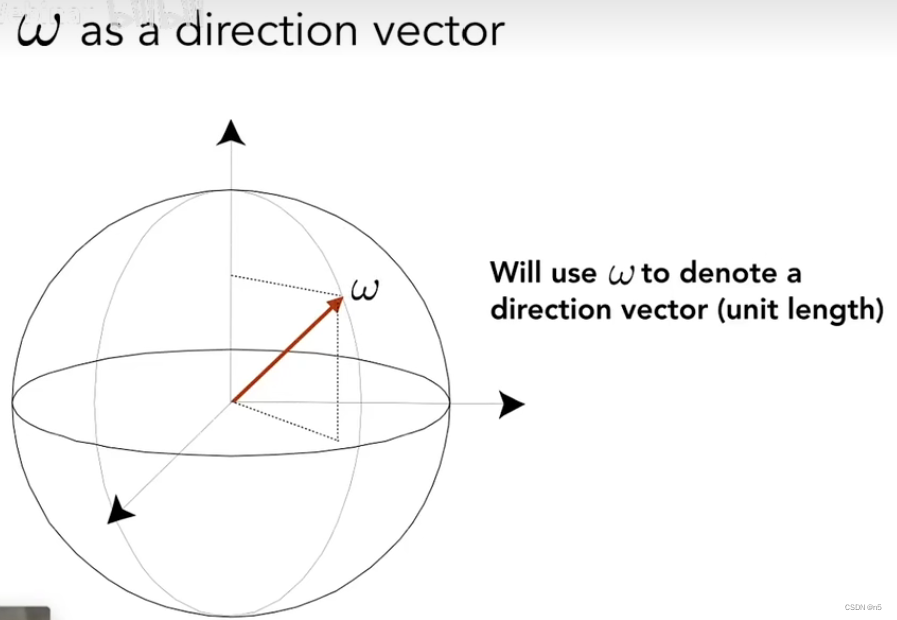
均匀点光源任意方向的Intensity的计算

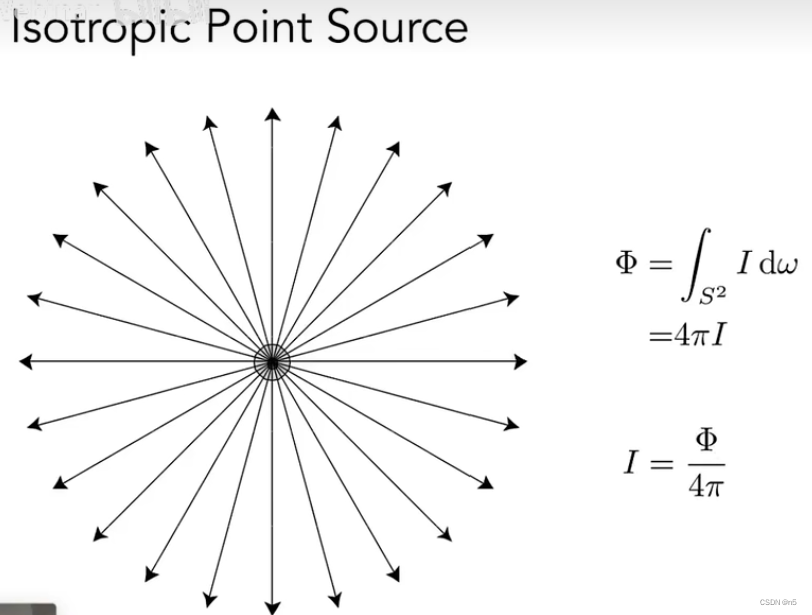
因为Intensity等于 $\frac{d\Phi }{d\omega }$，因此在球面上对Intensity进行积分得到的就是这个点光源的flux:
$$\Phi =4\pi I$$
因此对于均匀的点光源，其任意方向的Intensity是相同的，可以得到任意方向的Intensity为：
$$I=\frac{\Phi }{4\pi }$$

例子：LED灯泡

60W是相当于60W的白炽灯，但它实际是11W ，815流明。
假设该灯泡是均匀的（各向同性），那么它的Intensity是：
$$Intensity=\frac{815lumens}{4\pi }=65candelas$$

小结