目录

• 昨天上午的序列 - 30pts
• 今天上午的扫除 - 100pts
• 明天上午的教室 - 100pts
• 明天上午的数组 - 100pts
• 明天上午的函数 - 100pts

题目排序太合理了,EDCBA依次变难,导致我对着A题苦思冥想了半小时...

但是A题是[LeetCode 907. 子数组的最小值之和]的换皮题(除了题目一点没变)然鹅我还是做不出正解

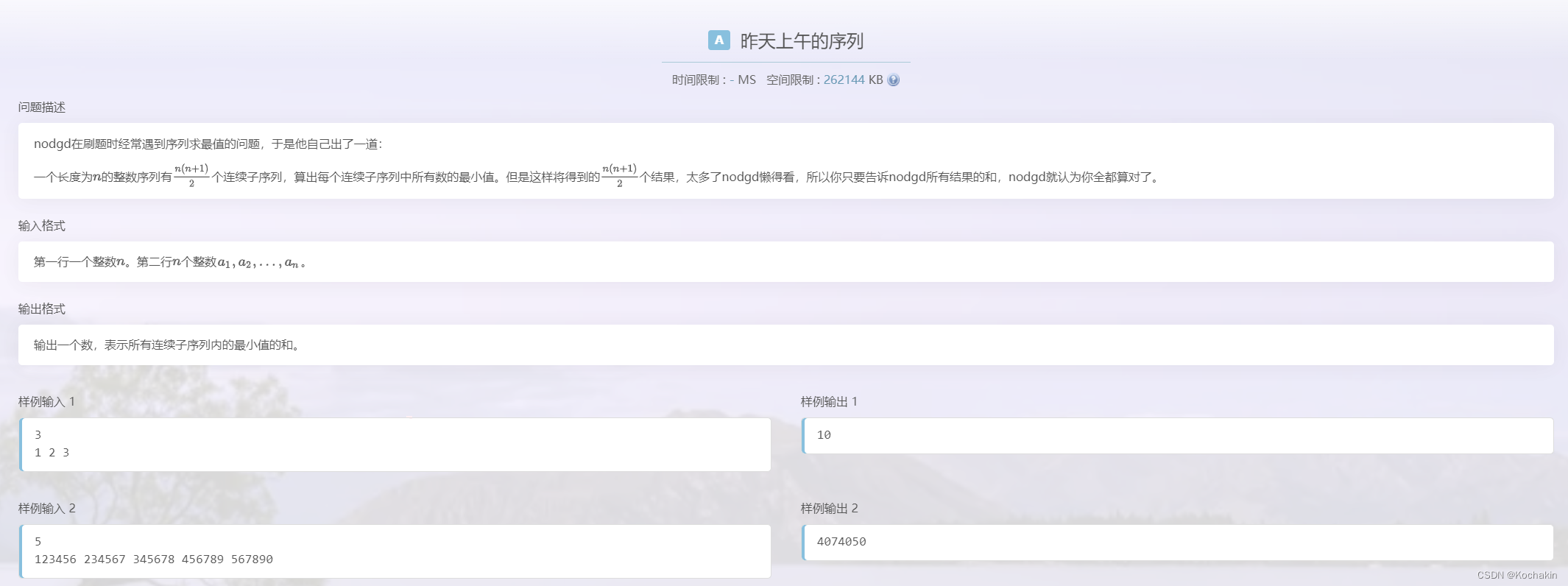
A-昨天上午的序列

这道题是一道单调栈的变式题；

首先经过推论我们可以得到对于一个数$a_k$,它会成为$l{l}_k\times r{r}_k\times a_k$个区间所容纳,其中$l{l}_k$是它左边连续的大于它的数的个数,$r{r}_k$是它右边连续的大于等于它的数的个数;

我们现在就是要快速求出他们的值,很简单,用两个结构体栈维护单调递增的序列和其对应的下标即可;注意我下面两个while循环当中的比较!!!不然会WA的很惨

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define int long long
using namespace std;
int n,a[200005],ans=0,ll[200005],rr[200005];
struct lyt{
	int num,xp;//数值,下标
};
stack<lyt> l,r; 
signed main(){
	scanf("%lld",&n);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}
	l.push((lyt){0LL,0LL});r.push((lyt){0LL,n+1});//初始化成这样可以省掉边界的特判
	for(int i=1;i<=n;i++){
		if(!l.empty()){while(l.top().num>a[i]){l.pop();}}
		ll[i]+=(i-l.top().xp);l.push((lyt){a[i],i});
	}//维护ll
	for(int i=n;i>=1;i--){
		if(!r.empty()){while(r.top().num>=a[i]){r.pop();}}
		rr[i]+=(r.top().xp-i);r.push((lyt){a[i],i});
	}//维护rr
	for(int i=1;i<=n;i++){ans+=ll[i]*rr[i]*a[i];}
	printf("%lld",ans);
	return 0;
}

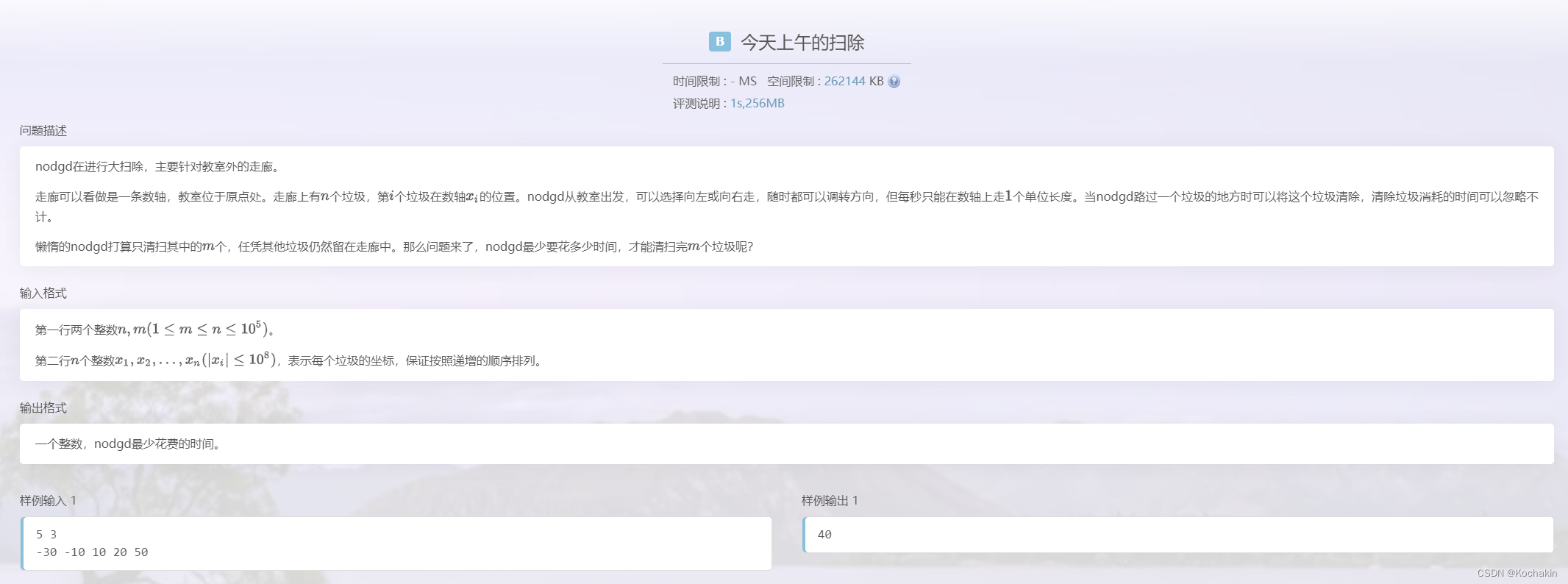
今天上午的扫除

这题非常之巧妙,关键在于这个人捡的垃圾肯定是连续的,我们可以证明,一旦捡的垃圾不连续,那么他一定会相对于连续的方案多走一些;

因而,我们只需要维护一个长度为$m$的区间,然后算出这个捡完区间的垃圾最短时间,而最短时间的计算方法无非两种:先捡负数或后捡负数,我们只需要分类讨论就可以了;

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define int long long
using namespace std;
int n,m,a[100005],minn=0x7fffffff,start;long long ans=0x7ffffffff;
signed main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){scanf("%lld",&a[i]);if(abs(a[i])<=minn){minn=abs(a[i]);start=i;}}if(a[start]<0){start++;}//start=最接近0的非负整数位置下标
	for(int l=1;l<=n-m+1;l++){
		int r=l+m-1;
		int z=max(r-start+1,0LL),f=max(start-l,0LL);//z=正(非负)数个数.f=负数个数
		if(z==0){ans=min(ans,abs(a[start-f]));}//只有负数垃圾
		else if(f==0){ans=min(ans,abs(a[start-1+z]));}//只有正数垃圾
		else{ans=min(ans,min(abs(a[start-1+z])+abs(a[start-1+z]-a[start-f]),abs(a[start-f])+abs(a[start-1+z]-a[start-f])));}//有正有负,分类讨论
	}printf("%lld",ans);
	return 0;
}

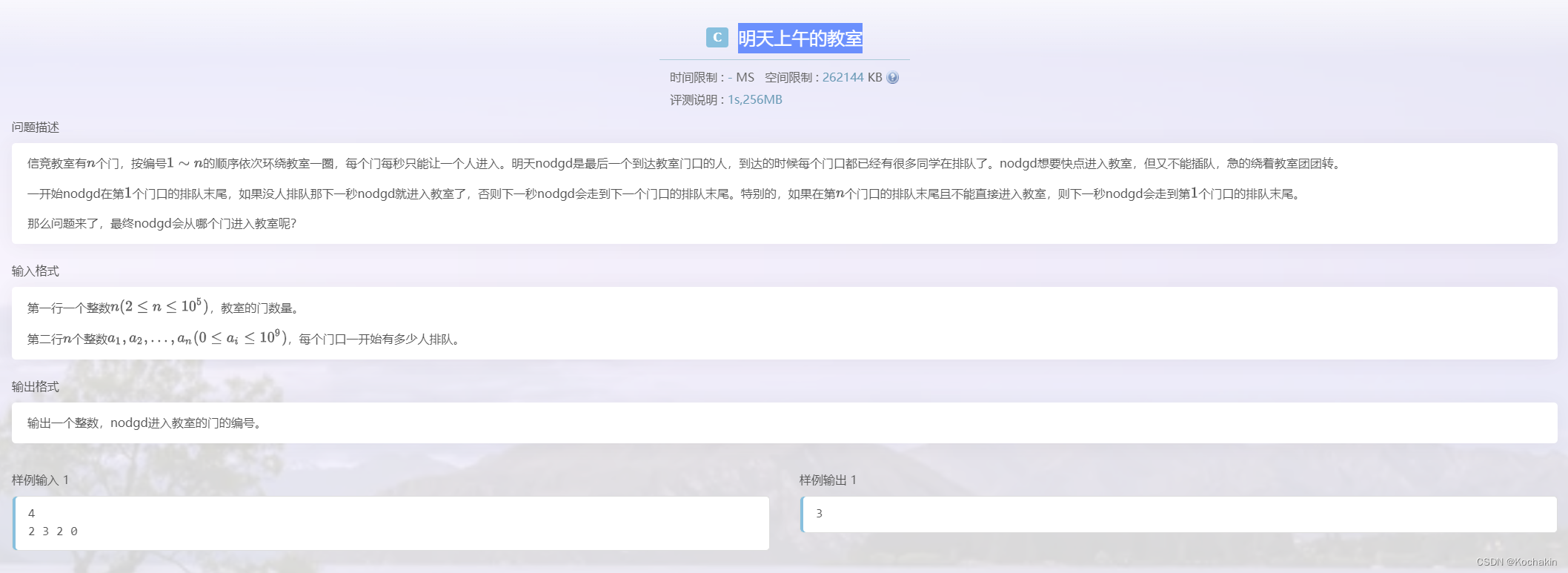
明天上午的教室

这道题的核心思路就是把人数转换成这个人在第几圈是可以进入这个门,方法就是:

void get(int i){
	if(!a[i]){
		num[i]=1LL;
	}else{
		int k=max(a[i]-i+1LL,0LL);if(k%n==0LL){num[i]=1+k/n;}
		else{num[i]=2LL+k/n;}
	}
	return;
}

其中num数组就是我们的第几圈的数组;这个函数的思想就是当这个人第一次到达这个门时有多少人,因为这个人下一次到这个门需要$n$秒,所以这个门会减少$n$人,以此内推;即可得到圈数;

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define int long long
using namespace std;
int n,a[100005],num[100005],minn=0x7ffffffff,ans;
void get(int i){
	if(!a[i]){
		num[i]=1LL;
	}else{
		int k=max(a[i]-i+1LL,0LL);if(k%n==0LL){num[i]=1+k/n;}
		else{num[i]=2LL+k/n;}
	}
	return;
}
signed main(){
	scanf("%lld",&n);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);get(i);}
	for(int i=1;i<=n;i++){if(num[i]<minn){minn=num[i];ans=i;}}
	printf("%lld",ans);
	return 0;
}

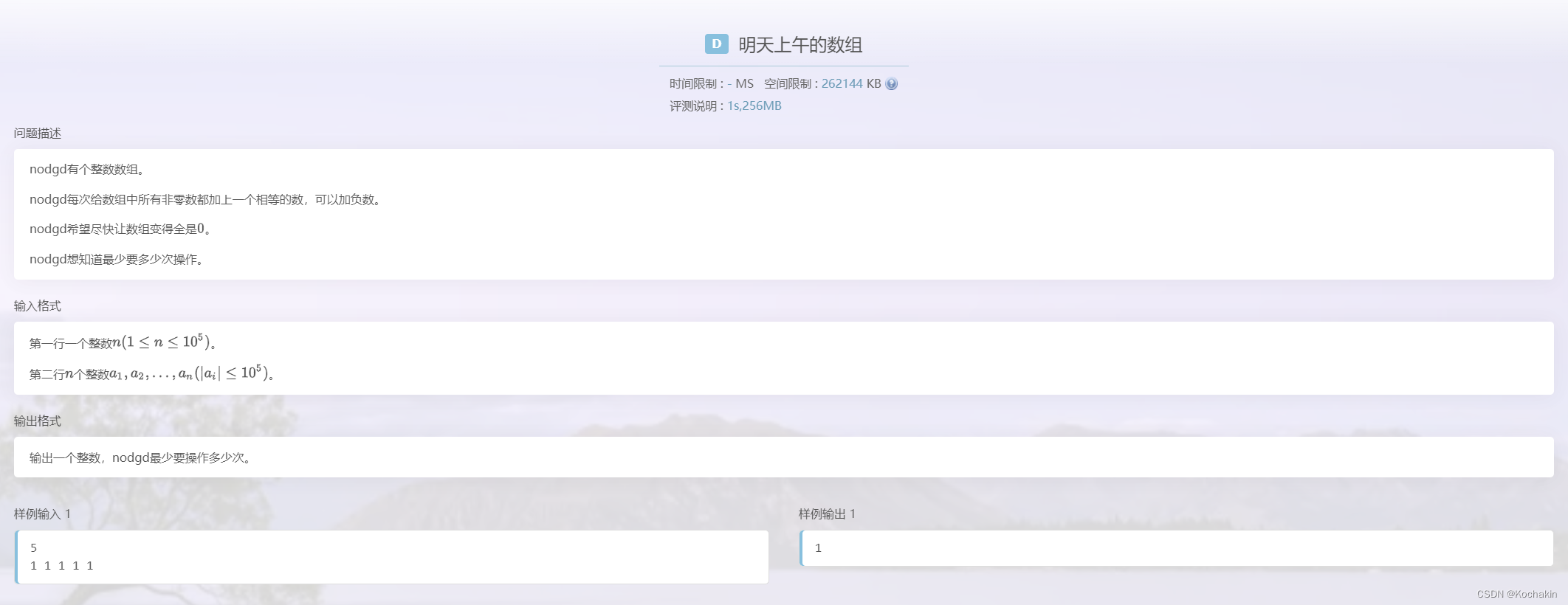
明天上午的数组

看起来很难,实际上只需要看数组中的有多少种不同的数字即可;

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define int long long
using namespace std;
int n,vis[200005],a[100005],ans;
signed main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);if(a[i]<0){a[i]=1e5+abs(a[i]);}else if(a[i]==0){continue;}
		if(!vis[a[i]]){vis[a[i]]=1;ans++;}
	}printf("%lld",ans);
	return 0;
}

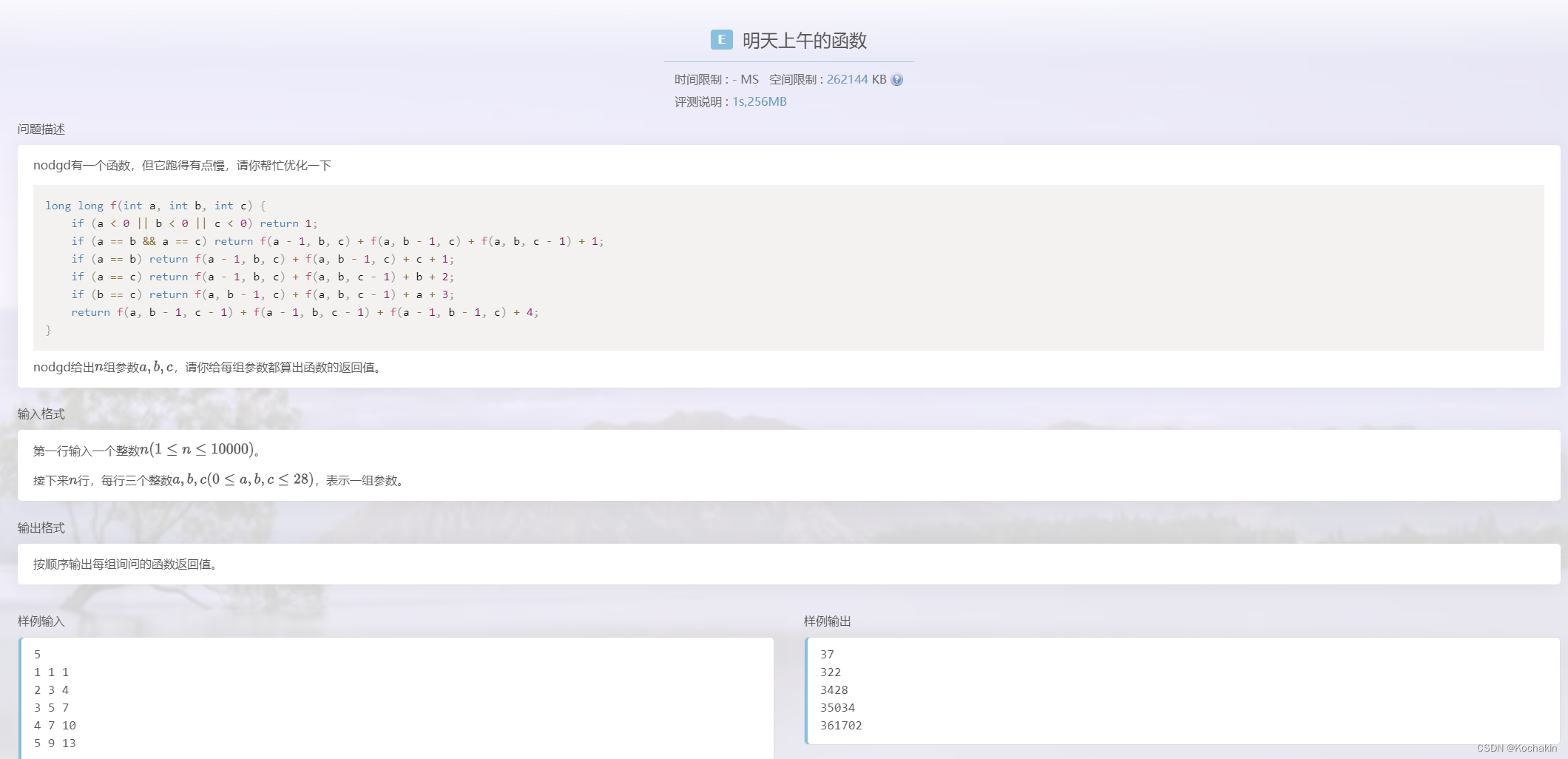
明天上午的函数

咳咳,给这个函数加上一个记忆化和O2优化就可以轻松卡过(似乎不是正解,但是的确可以过!

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define int long long
using namespace std;
int F[30][30][30],n,A,B,C;
long long f(int a, int b, int c) {
    if(a<0||b<0||c<0){return 1;}if(F[a][b][c]){return F[a][b][c];}
    if(a==b && a == c){return F[a][b][c]=f(a-1,b,c)+f(a,b-1,c)+f(a,b,c-1)+1;}
    if(a==b){return F[a][b][c]=f(a-1,b,c)+f(a,b-1,c)+c+1;}
    if(a==c){return F[a][b][c]=f(a-1,b,c)+f(a,b,c-1)+b+2;}
    if(b==c){return F[a][b][c]=f(a,b-1,c)+f(a,b,c-1)+a+3;}
    F[a][b][c]=f(a,b-1,c-1)+f(a-1,b,c-1)+f(a-1,b-1,c)+4;
    return F[a][b][c];
}
signed main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){scanf("%lld%lld%lld",&A,&B,&C);printf("%lld\n",f(A,B,C));}
	return 0;
}