目录链接：

力扣编程题-解法汇总_分享+记录-CSDN博客

GitHub同步刷题项目：

https://github.com/September26/java-algorithms

原题链接：力扣

描述：

给你两个长度可能不等的整数数组 nums1 和 nums2 。两个数组中的所有值都在 1 到 6 之间（包含 1 和 6）。

每次操作中，你可以选择 任意 数组中的任意一个整数，将它变成 1 到 6 之间 任意 的值（包含 1 和 6）。

请你返回使 nums1 中所有数的和与 nums2 中所有数的和相等的最少操作次数。如果无法使两个数组的和相等，请返回 -1 。

示例 1：

输入：nums1 = [1,2,3,4,5,6], nums2 = [1,1,2,2,2,2]
输出：3
解释：你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。
- 将 nums2[0] 变为 6 。 nums1 = [1,2,3,4,5,6], nums2 = [6,1,2,2,2,2] 。
- 将 nums1[5] 变为 1 。 nums1 = [1,2,3,4,5,1], nums2 = [6,1,2,2,2,2] 。
- 将 nums1[2] 变为 2 。 nums1 = [1,2,2,4,5,1], nums2 = [6,1,2,2,2,2] 。

示例 2：

输入：nums1 = [1,1,1,1,1,1,1], nums2 = [6]
输出：-1
解释：没有办法减少 nums1 的和或者增加 nums2 的和使二者相等。

示例 3：

输入：nums1 = [6,6], nums2 = [1]
输出：3
解释：你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。
- 将 nums1[0] 变为 2 。 nums1 = [2,6], nums2 = [1] 。
- 将 nums1[1] 变为 2 。 nums1 = [2,2], nums2 = [1] 。
- 将 nums2[0] 变为 4 。 nums1 = [2,2], nums2 = [4] 。

提示：

• 1 <= nums1.length, nums2.length <= 105
• 1 <= nums1[i], nums2[i] <= 6

解题思路：

* 解题思路：
* 用两个数组，分别装在nums1和nums2中1到6每个数组的数量，比如nums1[4]就代表nums1中5的数量。
* 如果使用compare方法来寻找最少操作次数，保证前面那个是大的，后面那个是小的。
* compare方法中，分别尝试操作intsBig和intsSmall,
* 等于说首先尝试把intsBig中的6改1，如果dValue>0，则说明不够，继续尝试把intsSmall中的1改为6，再求dValue。
* 如果dValue>0，则尝试5，继续循环下去

代码：

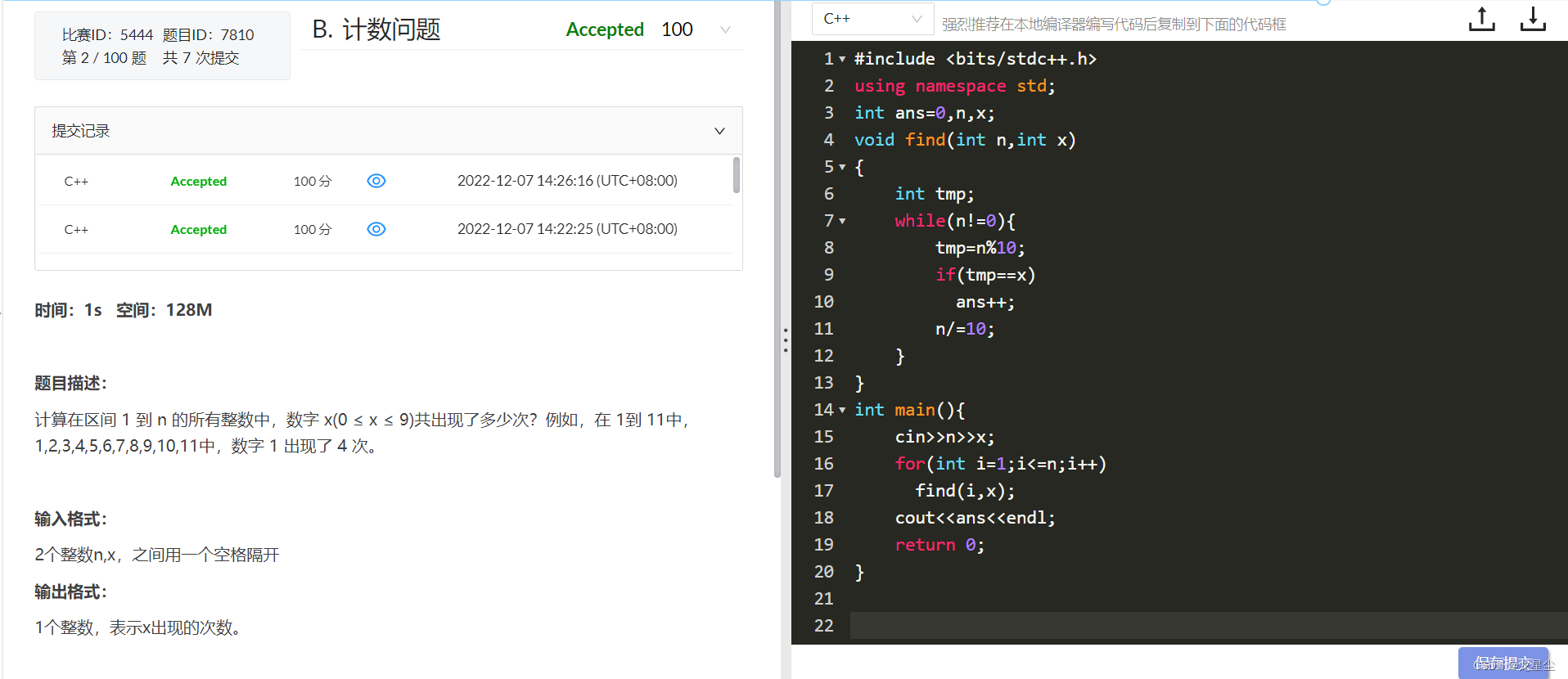
public class Solution1775 {

    public int minOperations(int[] nums1, int[] nums2) {
        int sum1 = 0;
        int sum2 = 0;
        int[] ints1 = new int[6];
        int[] ints2 = new int[6];
        for (int i1 : nums1) {
            sum1 += i1;
            ints1[i1 - 1]++;
        }
        for (int i2 : nums2) {
            sum2 += i2;
            ints2[i2 - 1]++;
        }
        if (sum1 == sum2) {
            return 0;
        }
        if (sum1 > sum2) {
            return compare(sum1, sum2, ints1, ints2);
        }
        return compare(sum2, sum1, ints2, ints1);
    }

    private int compare(int sumBig, int sumSmall, int[] intsBig, int[] intsSmall) {
        int dValue = sumBig - sumSmall;
        int times = 0;
        for (int i = 0; i < intsBig.length - 1; i++) {
            int num = intsBig[5 - i];
            if (num > 0) {
                if (dValue > (5 - i) * num) {
                    times += num;
                    dValue -= ((5 - i) * num);
                } else {
                    int i1 = dValue / (5 - i);
                    times += (dValue % (5 - i) == 0 ? i1 : i1 + 1);
                    return times;
                }
            }
            //6,5,4
            num = intsSmall[i];
            if (num > 0) {
                if (dValue > (5 - i) * num) {
                    times += num;
                    dValue -= ((5 - i) * num);
                } else {
                    int i1 = dValue / (5 - i);
                    times += (dValue % (5 - i) == 0 ? i1 : i1 + 1);
                    return times;
                }
            }
        }
        return -1;
    }

}