C++ 用红黑树封装map/set

前言

一、源码结构分析

二、模拟实现map/set

2.1 套上KeyOfT

2.2 普通迭代器实现

2.3 const迭代器实现

2.4 解决key不能修改的问题

2.5 map的[]实现

2.6 map/set以及红黑树源码

2.6.1 RBTree.h

2.6.2 set.h

2.6.3 map.h

总结

前言

之前的文章讲解了红黑树的具体实现，本篇文章就用红黑树来封装一个map/set出来，但是大家在实现前一定要保证红黑树不要出现问题，如果红黑树有问题还是要先把红黑树调好再来实现封装。

一、源码结构分析

以下源码来自SGI-STL3.0版本，map和set的源代码在map/set/stl_map.h/stl_set.h/stl_tree.h等⼏个头文件中，下面是截取的一部分核心代码

// stl_set.h
template <class Key, class Compare = less<Key>, class Alloc = alloc>
class set {
public:
	typedef Key key_type;
	typedef Key value_type;
private:
	typedef rb_tree<key_type, value_type,
		identity<value_type>, key_compare, Alloc> rep_type;
	rep_type t;
};

// stl_map.h
template <class Key, class T, class Compare = less<Key>, class Alloc = alloc>
class map {
public:		
	typedef Key key_type;
	typedef T mapped_type;
	typedef pair<const Key, T> value_type;

private:
	typedef rb_tree<key_type, value_type,
		select1st<value_type>, key_compare, Alloc> rep_type;
	rep_type t;
};

// stl_tree.h
struct __rb_tree_node_base
{
	typedef __rb_tree_color_type color_type;
	typedef __rb_tree_node_base* base_ptr;

	color_type color;
	base_ptr parent;
	base_ptr left;
	base_ptr right;
};

// stl_tree.h
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc>
class rb_tree {
protected:
	typedef void* void_pointer;
	typedef __rb_tree_node_base* base_ptr;
	typedef __rb_tree_node<Value> rb_tree_node;
	typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator;
	typedef __rb_tree_color_type color_type;
public:
	typedef Key key_type;
	typedef Value value_type;
	typedef value_type* pointer;
	typedef const value_type* const_pointer;
	typedef value_type& reference;
	typedef const value_type& const_reference;
	typedef rb_tree_node* link_type;
	typedef size_t size_type;
	typedef ptrdiff_t difference_type;
protected:
	size_type node_count; // keeps track of size of tree
	link_type header;
	Compare key_compare;
};

// stl_tree.h
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
	typedef __rb_tree_node<Value>* link_type;
	Value value_field;
};

通过上图的分析，可以看到源码中rb_tree用了一个泛型的思想来实现，rb_tree是实现key的搜索场景，还是key/value的搜索场景不是直接写死的，而是第二个模板参数Value决定_rb_tree_node中存储的数据类型。

set实例化rb_tree时第二个模板参数给的是key，map实例化rb_tree时第二个模板参数给的是

pair<const key, T>，这样一颗红黑树既可以实现key搜索场景的set，也可以实现key/value搜索场

景的map。

也就是说对于set来说，Key是Key，Value也是Key，对于map来说，Key是Key，Value是pair，而rb_tree的第二个模版参数Value才是真正存在节点里面的，所以set在节点中存的就是一个Key，map在节点中存的是pair。

那既然rb_tree第二个模板参数Value已经控制了红黑树结点中存储的数据类型，为什么还要传第一个模板参数Key呢？其实是因为在find/erase时的函数参数都是Key，所以第⼀个模板参数是传给find/erase等函数做形参的类型的。

那我们自己的map/set以及红黑树的修改就如下：

namespace hx
{
	template<class K>
	class set
	{
	public:
	private:
		RBTree<K, K> _t;
	};
}

namespace hx
{
	template<class K, class V>
	class map
	{
	public:
	private:
		RBTree<K, pair<K, V>> _t;
	};
}

enum Color
{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	T _data;
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	Color _col;

	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{}
};

template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;
public:
private:
	Node* _root = nullptr;
};

二、模拟实现map/set

模拟实现一共分为五步：

1、套上KeyOfT

2、普通迭代器

3、const迭代器

4、解决Key不能修改的问题

5、map的[]实现

2.1 套上KeyOfT

既然已经知道了红黑树的第二个模版参数才是存在节点里的，那先对红黑树以及节点类进行一个修改

template<class T>
struct RBTreeNode
{
	T _data;
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	Color _col;

	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{}
};

template<class K, class T>
struct RBTree
{
	typedef RBTreeNode<T> Node;
public:
	bool insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;

			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
            // 问题出现了
			if (cur->_data < data)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_data > data)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

将节点类修改成一个模版参数T，insert的参数也是插入一个key，但是在cur中的_data与形参data比较的时候问题就来了，如果data是key，那么直接比较没问题，但是如果是一个pair呢？库中虽然重载了pair的比较大小，但是库中的比较方式是，first大就大，如果first相等，那second大就大，如果first和second都相等，这两个pair对象才相同。这显然不符合我们的需求，我们要的是如果first相等，那两个pair对象就是相等，那就需要上一个仿函数来自己控制这里的比较逻辑。

但是又没有办法在红黑树中写仿函数，因为对于下层来说，根本就不知道节点中存储的数据类型是什么，那下层不知道，但是上层知道，所以就可以在map和set中定义仿函数，作为模版参数传进来，通过仿函数去取出对象里面的key。

namespace hx
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
	private:
		RBTree<K, K, SetKeyOfT> _t;
	};
}

namespace hx
{
	template<class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
	private:
		RBTree<K, pair<K, V>, MapKeyOfT> _t;
	};
}

template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;
public:
	bool insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;

			return true;
		}
        
        // 定义对象
		KeyOfT kot;
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{    
            // 去取里面的key
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
            // 去取里面的key
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(data);
		Node* newnode = cur;

		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
        // ...
        // 还有很多代码，但是在这里只留下需要修改的部分
    }
};

这样就完美的解决了问题，用一个模版参数，data中存的是Key，就去把这个Key取出来，存的是pair，就去把这个pair中的Key取出来。map和set的insert直接就去调用树的insert。

// set
namespace hx
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		bool insert(const K& key)
		{
			return _t.insert(key);
		}
	private:
		RBTree<K, K, SetKeyOfT> _t;
	};
}

// map
namespace hx
{
	template<class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		bool insert(const pair<K, V>& kv)
		{
			return _t.insert(kv);
		}
	private:
		RBTree<K, pair<K, V>, MapKeyOfT> _t;
	};
}

2.2 普通迭代器实现

iterator实现的大体框架跟list的iterator思路是一致的，用一个类型封装结点的指针，再通过重载运算符实现，迭代器像指针一样访问的行为。

这里的难点是operator++和operator--的实现。map和set的迭代器走的是中序遍历，左子树->根结点->右子树，那么begin()会返回中序第一个结点的迭代器，也就是最左节点。

迭代器++的核心逻辑就是不看全局，只看局部，只考虑当前中序局部要访问的下一个结点。

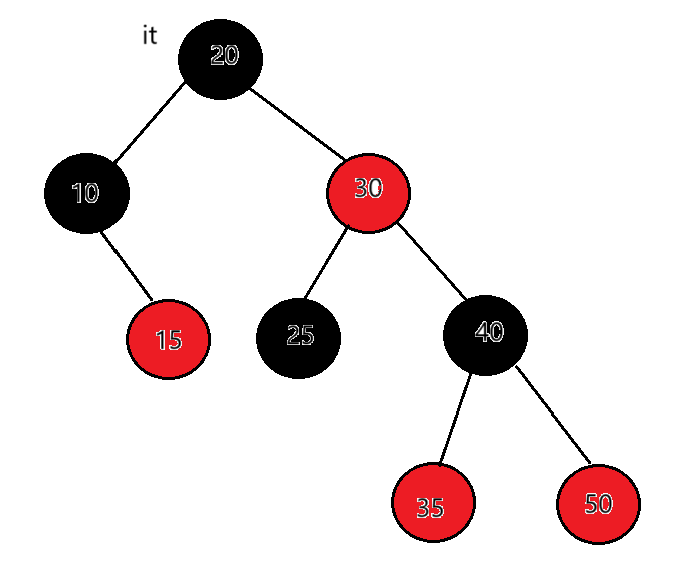
迭代器++时，如果it指向的结点的右子树不为空，代表当前结点已经访问完了，因为是左根右，左子树和根已经访问完了，要去访问右子树了，要访问下一个结点是右子树的中序第一个，一棵树中序第一个是最左结点，所以直接找右子树的最左结点即可。

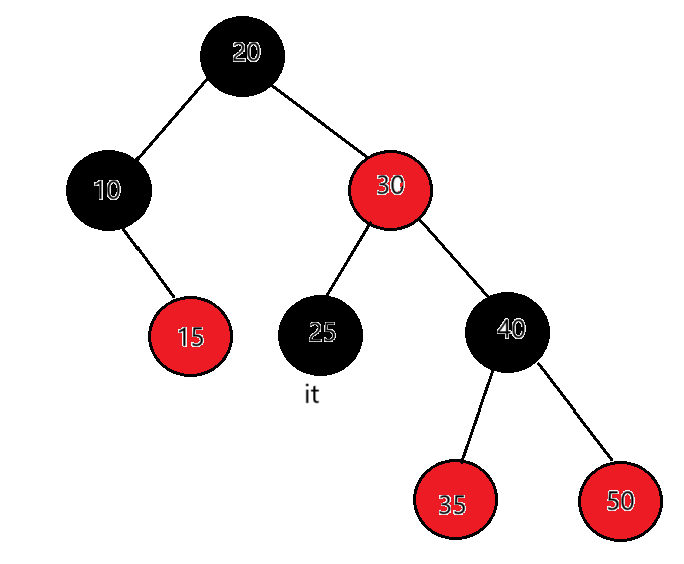
迭代器++时，如果it指向的结点的右子树为空，代表当前结点已经访问完了，且当前结点所在的子树也访问完了，要访问的下一个结点在当前结点的祖先里面，所以要沿着当前结点到根的祖先路径向上找。例如：25的右子树为空，以25做根的这棵局部子树就访问完了，要看当前节点25在父亲的哪里，父亲是30，25是30的左，那就说明下一个要访问的节点就是父亲所在的节点30。

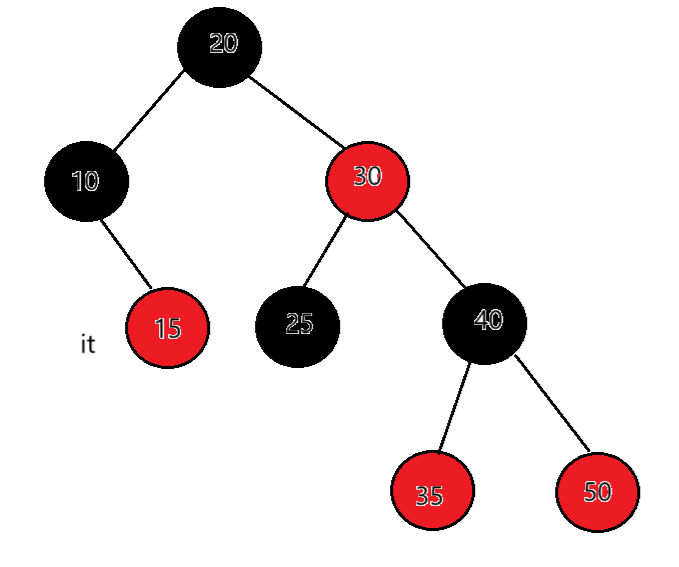
如果当前结点是父亲的右，根据中序左子树->根结点->右子树，当前结点所在的子树访问完 了，当前结点所在父亲的子树也访问完了，那么下一个访问的需要继续往根的祖先中去找，直到找 到孩子是父亲左的那个祖先就是中序要问题的下一个结点。例如：it指向15，15右为空，父亲是10，15是10的右，15所在的子树访问完了，10所在的子树也访问完了，继续往上找，父亲是20，10是20的左，那么下一个访问的结点就是18。

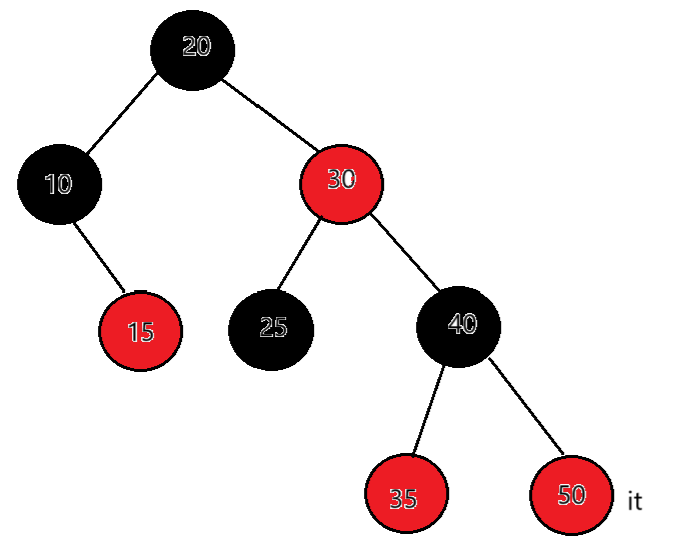
如果it在50，50的右为空，50为根的这棵子树访问完了，父亲是40，50是40的右，说明40所在的子树访问完了。继续向上从祖先中找，当前节点是40，父亲是30，40是30的右，说明30所在的子树访问完了。当前节点是30，父亲是20，30是20的右，说明20所在的子树访问完了。当前节点是20，父亲是空。结束遍历。

总结：当右子树不为空时，下一个要访问的节点就是右子树的最左节点，当右子树为空时，看当前节点在父亲的左还是右，如果在父亲的左，下一个要访问的节点就是父亲，如果在父亲的右，那就要到当前节点的祖先中去查找，直到找到孩子是父亲左的那个祖先就是要访问的下一个结点，如果父亲为空了，那整棵树就遍历完了，也让当前节点去指向父亲。end()的结束我们定义成走到空就是结束。

template<class T>
struct __RBTree_Iterator
{
	typedef __RBTree_Iterator<T> Self;
	typedef RBTreeNode<T> Node;
	Node* _node;

	__RBTree_Iterator(Node* node)
		:_node(node)
	{}

	Self& operator++()
	{    
        // 右子树不为空
		if (_node->_right)
		{
			_node = _node->_right;
            // 找右子树的最左节点
			while (_node->_left)
			{
				_node = _node->_left;
			}
		}
		else
		{
            // 右子树为空
			Node* cur = _node;
			Node* parent = cur->_parent;
            // 循环的找，当找到孩子是父亲的左时，父亲就是下一个要访问的节点
			while (parent && parent->_right == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}
            

            // 无论是因为孩子是父亲的左，还是因为父亲为空了，下一个要访问的节点都是parent
			_node = parent;
		}

		return *this;
	}

};

迭代器--也是一样的道理，只不过就是反过来，按照右子树->根->左子树的顺序遍历。当左子树不为空时，下一个要访问的节点就是左子树的最右节点，当左子树为空时，看当前节点在父亲的左还是右，如果在父亲的右，下一个要访问的节点就是父亲，如果在父亲的左，那就要到当前节点的祖先中去查找，直到找到孩子是父亲右的那个祖先就是要访问的下一个结点，如果父亲为空了，那整棵树就遍历完了，也让当前节点去指向父亲。

Self& operator--()
{
	if (_node->_left)
	{
		_node = _node->_left;
		while (_node->_right)
		{
			_node = _node->_right;
		}
	}
	else
	{
		Node* cur = _node;
		Node* parent = cur->_parent;
		while (parent && parent->_left == cur)
		{
			cur = parent;
			parent = parent->_parent;
		}

		_node = parent;
	}

	return *this;
}

那++和--实现完了，其他的就和list的迭代器是一样的了，我们把其余功能补全

template<class T>
struct __RBTree_Iterator
{
	typedef __RBTree_Iterator<T> Self;
	typedef RBTreeNode<T> Node;
	Node* _node;

	__RBTree_Iterator(Node* node)
		:_node(node)
	{}

	T& operator*()
	{
		return _node->_data;
	}

	T* operator->()
	{
		return &_node->_data;
	}

	Self& operator++()
	{
		// 右子树不为空
		if (_node->_right)
		{
			_node = _node->_right;
			// 找右子树的最左节点
			while (_node->_left)
			{
				_node = _node->_left;
			}
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			// 循环的找，当找到孩子是父亲的左时，父亲就是下一个要访问的节点
			while (parent && parent->_right == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			// 无论是因为孩子是父亲的左，还是因为父亲为空了，下一个要访问的节点都是parent
			_node = parent;
		}

		return *this;
	}

	Self operator++(int)
	{
		Self tmp = *this;
		++*this;

		return tmp;
	}

	Self& operator--()
	{
		if (_node->_left)
		{
			_node = _node->_left;
			while (_node->_right)
			{
				_node = _node->_right;
			}
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && parent->_left == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

	Self operator--(int)
	{
		Self tmp = *this;
		--*this;

		return tmp;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}

	bool operator==(const Self& s)
	{
		return _node == s._node;
	}
};

template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef __RBTree_Iterator<T> iterator;

	iterator begin()
	{
		Node* minleft = _root;
		while (minleft && minleft->_left)
		{
			minleft = minleft->_left;
		}

		return minleft;
	}

	iterator end()
	{
		return nullptr;
	}
};

下层实现好了要继续来实现上层

namespace hx
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
        // 要加上typename
		typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		bool insert(const K& key)
		{
			return _t.insert(key);
		}

	private:
		RBTree<K, K, SetKeyOfT> _t;
	};
}

这里一定要注意，在取红黑树里面的迭代器时，属于类模版中取内嵌类型，一定要加上typename，因为编译器不知道这里的iterator是类型还是对象，加上typename就是告诉编译器是类型，等模版实例化了再去找。map也是同理。

namespace hx
{
	template<class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
        // 一定要加typename
		typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		bool insert(const pair<K, V>& kv)
		{
			return _t.insert(kv);
		}

	private:
		RBTree<K, pair<K, V>, MapKeyOfT> _t;
	};
}

2.3 const迭代器实现

我们知道普通迭代器和const迭代器的不同就是在operator*和operator->的返回值，和list一样，其他不变就好了

template<class T, class Ref, class Ptr>
struct __RBTree_Iterator
{
	typedef __RBTree_Iterator<T, Ref, Ptr> Self;
	typedef RBTreeNode<T> Node;
	Node* _node;

	__RBTree_Iterator(Node* node)
		:_node(node)
	{}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &_node->_data;
	}

	Self& operator++()
	{
		// 右子树不为空
		if (_node->_right)
		{
			_node = _node->_right;
			// 找右子树的最左节点
			while (_node->_left)
			{
				_node = _node->_left;
			}
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			// 循环的找，当找到孩子是父亲的左时，父亲就是下一个要访问的节点
			while (parent && parent->_right == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			// 无论是因为孩子是父亲的左，还是因为父亲为空了，下一个要访问的节点都是parent
			_node = parent;
		}

		return *this;
	}

	Self operator++(int)
	{
		Self tmp = *this;
		++*this;

		return tmp;
	}

	Self& operator--()
	{
		if (_node->_left)
		{
			_node = _node->_left;
			while (_node->_right)
			{
				_node = _node->_right;
			}
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && parent->_left == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

	Self operator--(int)
	{
		Self tmp = *this;
		--*this;

		return tmp;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}

	bool operator==(const Self& s)
	{
		return _node == s._node;
	}
};

template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef __RBTree_Iterator<T, T&, T*> iterator;
	typedef __RBTree_Iterator<T, const T&, const T*> const_iterator;

	iterator begin()
	{
		Node* minleft = _root;
		while (minleft && minleft->_left)
		{
			minleft = minleft->_left;
		}

		return minleft;
	}

	iterator end()
	{
		return nullptr;
	}

	const_iterator begin() const
	{
		Node* minleft = _root;
		while (minleft && minleft->_left)
		{
			minleft = minleft->_left;
		}

		return minleft;
	}

	const_iterator end() const
	{
		return nullptr;
	}
};

namespace hx
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;
		typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		const_iterator begin() const
		{
			return _t.begin();
		}

		const_iterator end() const
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const K& key)
		{
			return _t.insert(key);
		}

	private:
		RBTree<K, K, SetKeyOfT> _t;
	};
}

namespace hx
{
	template<class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;
		typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::const_iterator const_iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		const_iterator begin() const
		{
			return _t.begin();
		}

		const_iterator end() const
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const pair<K, V>& kv)
		{
			return _t.insert(kv);
		}

	private:
		RBTree<K, pair<K, V>, MapKeyOfT> _t;
	};
}

2.4 解决key不能修改的问题

在map和set中，key是不能修改的，map的value可以修改，在key前加上const修饰即可

namespace hx
{
	template<class K>
	class set
	{
	public:
		typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;
		typedef typename RBTree<K, const K, SetKeyOfT>::const_iterator const_iterator;
	private:
		RBTree<K, const K, SetKeyOfT> _t;
	};
}

namespace hx
{
	template<class K, class V>
	class map
	{
	public:
		typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
		typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;
	private:
		RBTree<K, pair<const K, V>, MapKeyOfT> _t;
	};
}

注意map中，const可不要加在pair前面了，加在pair前面那就是first和second都不能修改，但我们要的只是first不能修改。

2.5 map的[]实现

[]中要调用insert，所以要先把insert的返回值修改成pair<iterator, bool>类型

pair<iterator, bool> insert(const T& data)
{
	if (_root == nullptr)
	{
		_root = new Node(data);
		_root->_col = BLACK;
        
		return { _root, true };
	}

	// 定义对象
	KeyOfT kot;
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		// 去取里面的key
		if (kot(cur->_data) < kot(data))
		{
			parent = cur;
			cur = cur->_right;
		}
		// 去取里面的key
		else if (kot(cur->_data) > kot(data))
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return { cur, false };
		}
	}

	cur = new Node(data);
    // 重新定义出来一个节点newnode
	Node* newnode = cur;

	if (kot(parent->_data) < kot(data))
	{
		parent->_right = cur;
	}
	else
	{
		parent->_left = cur;
	}

	cur->_parent = parent;
	cur->_col = RED;

	// ... 调平衡

	_root->_col = BLACK;

	return { newnode, true };
}

如果根为空就，就返回{_root, true}，代表插入成功，如果值已经存在，就返回已经存在的节点{cur, false}，如果根不为空，也没有这个值，返回的节点指针一定不要用cur，因为在调整平衡的时候cur可能已经不知道走到哪去了，提前记录一个newnode，用{newnode, true}返回。

// set
pair<iterator, bool> insert(const K& key)
{
	return _t.insert(key);
}

// map
pair<iterator, bool> insert(const pair<K, V>& kv)
{
	return _t.insert(kv);
}

V& operator[](const K& key)
{
	pair<iterator, bool> ret = _t.insert({ key, V() });
	return ret.first->second;
}

[]的实现是先去调用insert，插入一个value的匿名对象就可以，会去调用value的默认构造，并且接收返回值，ret.first拿到的就是迭代器对象，里面存储的就是节点的指针，不管这个key是之前就存在，还是新插入进去的，都是这个节点的指针，迭代器对象去调用operator->拿到pair的地址，再解引用拿second，为了可读性两个->省略成了一个。

2.6 map/set以及红黑树源码

2.6.1 RBTree.h


{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	T _data;
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	Color _col;

	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{}
};

template<class T, class Ref, class Ptr>
struct __RBTree_Iterator
{
	typedef __RBTree_Iterator<T, Ref, Ptr> Self;
	typedef RBTreeNode<T> Node;
	Node* _node;

	__RBTree_Iterator(Node* node)
		:_node(node)
	{}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &_node->_data;
	}

	Self& operator++()
	{
		// 右子树不为空
		if (_node->_right)
		{
			_node = _node->_right;
			// 找右子树的最左节点
			while (_node->_left)
			{
				_node = _node->_left;
			}
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			// 循环的找，当找到孩子是父亲的左时，父亲就是下一个要访问的节点
			while (parent && parent->_right == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			// 无论是因为孩子是父亲的左，还是因为父亲为空了，下一个要访问的节点都是parent
			_node = parent;
		}

		return *this;
	}

	Self operator++(int)
	{
		Self tmp = *this;
		++*this;

		return tmp;
	}

	Self& operator--()
	{
		if (_node->_left)
		{
			_node = _node->_left;
			while (_node->_right)
			{
				_node = _node->_right;
			}
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && parent->_left == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

	Self operator--(int)
	{
		Self tmp = *this;
		--*this;

		return tmp;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}

	bool operator==(const Self& s)
	{
		return _node == s._node;
	}
};

template<class K, class T, class KeyOfT>
struct RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef __RBTree_Iterator<T, T&, T*> iterator;
	typedef __RBTree_Iterator<T, const T&, const T*> const_iterator;

	iterator begin()
	{
		Node* minleft = _root;
		while (minleft && minleft->_left)
		{
			minleft = minleft->_left;
		}

		return minleft;
	}

	iterator end()
	{
		return nullptr;
	}

	const_iterator begin() const
	{
		Node* minleft = _root;
		while (minleft && minleft->_left)
		{
			minleft = minleft->_left;
		}

		return minleft;
	}

	const_iterator end() const
	{
		return nullptr;
	}

	pair<iterator, bool> insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;

			return { _root, true };
		}

		// 定义对象
		KeyOfT kot;
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			// 去取里面的key
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			// 去取里面的key
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return { cur, false };
			}
		}

		cur = new Node(data);
		Node* newnode = cur;

		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}

		cur->_parent = parent;
		cur->_col = RED;

		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;

				// 调整
				if (uncle && uncle->_col == RED) // 叔叔存在且为红
				{
					// 变色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续向上调整
					cur = grandfather;
					parent = cur->_parent;
				}
				else // 叔叔不存在或叔叔存在且为黑
				{
					if (parent->_left == cur)
					{
						RotateR(grandfather);
						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						grandfather->_col = RED;
						cur->_col = BLACK;
					}

					break; // 旋转完子树平衡，不需要继续调整
				}
			}
			else //grandfather->_right == parent
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED) // 叔叔存在且为红
				{
					parent->_col = uncle->_col = BLACK; // 变色
					grandfather->_col = RED;

					// 继续向上调整
					grandfather = cur;
					parent = cur->_parent;
				}
				else // 叔叔不存在或叔叔存在且为黑
				{
					if (parent->_right == cur)
					{
						RotateL(grandfather);
						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						grandfather->_col = RED;
						cur->_col = BLACK;
					}

					break; // 旋转完子树平衡，不需要继续调整
				}
			}
		}

		_root->_col = BLACK;

		return { newnode, true };
	}

	void RotateR(Node* parent)
	{
		Node* cur = parent->_left;
		Node* curright = cur->_right;

		parent->_left = curright;
		if (curright)
			curright->_parent = parent;

		cur->_right = parent;

		Node* parentParent = parent->_parent;
		parent->_parent = cur;

		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = cur;
			}
			else
			{
				parentParent->_right = cur;
			}

			cur->_parent = parentParent;
		}
	}

	void RotateL(Node* parent)
	{
		Node* cur = parent->_right;
		Node* curleft = cur->_left;

		parent->_right = curleft;

		if (curleft)
			curleft->_parent = parent;

		cur->_left = parent;

		Node* parentParent = parent->_parent;
		parent->_parent = cur;

		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = cur;
			}
			else
			{
				parentParent->_right = cur;
			}

			cur->_parent = parentParent;
		}
	}

	bool find(const K& key)
	{
		KeyOfT kot;
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) < key)
			{
				cur = cur->_right;
			}
			else if (kot(cur->_data) > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}

		return false;
	}

	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}

	int Height()
	{
		return _Height(_root);
	}

	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;

		int retleft = _Height(root->_left);
		int retright = _Height(root->_right);

		return retleft > retright ? retleft + 1 : retright + 1;
	}

	int size()
	{
		return _size(_root);
	}

	int _size(Node* root)
	{
		if (root == nullptr)
			return 0;

		return _size(root->_left) + _size(root->_right) + 1;
	}

	bool Check(Node* root, int refersum, int cursum)
	{
		if (root == nullptr)
		{
			// 走到空与基准值refersum作比较，检查规则四
			if (refersum != cursum)
			{
				cout << "每条路径上黑色节点的数量不相等" << endl;
				return false;
			}
			return true;
		}

		// 检查规则三
		if (root->_col == RED && root->_parent && root->_parent->_col == RED)
		{
			cout << "出现连续的红色节点" << endl;
			return false;
		}

		// 遇到黑色节点就++
		if (root->_col == BLACK)
			cursum++;

		// 继续递归去检查
		return Check(root->_left, refersum, cursum)
			&& Check(root->_right, refersum, cursum);
	}

	bool isBalance()
	{
		// 空树也是红黑树
		if (_root == nullptr)
			return true;

		// 检查规则二
		if (_root->_col == RED)
			return false;

		// 用最左边的路径作为参考值
		int BlackSum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				BlackSum++;

			cur = cur->_left;
		}

		return Check(_root, BlackSum, 0);
	}

private:
	Node* _root = nullptr;
};

2.6.2 set.h

namespace hx
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;
		typedef typename RBTree<K, const K, SetKeyOfT>::const_iterator const_iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		const_iterator begin() const
		{
			return _t.begin();
		}

		const_iterator end() const
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const K& key)
		{
			return _t.insert(key);
		}

	private:
		RBTree<K, const K, SetKeyOfT> _t;
	};
}

2.6.3 map.h

namespace hx
{
	template<class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
		typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		const_iterator begin() const
		{
			return _t.begin();
		}

		const_iterator end() const
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const pair<K, V>& kv)
		{
			return _t.insert(kv);
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = _t.insert({ key, V() });
			return ret.first->second;
		}

	private:
		RBTree<K, pair<const K, V>, MapKeyOfT> _t;
	};
}

总结

本篇文章讲的非常细致，一步一步去实现，没有跨越什么，大家在实现的时候也一定要一步一步的来，写完这一步，测试没有问题了，再去搞下一步，不要想着一口吃个胖子，可千万不要出现最后功能都实现好了，结果红黑树的实现有问题这种情况。对于map和set我们实现这些功能就可以了，那如果大家觉得小编写的还不错，可以给小编一个三连表示支持！！！感谢大家！