【MIKE水动力】MIKE11基本原理(上)

news2025/2/25 7:38:13

Mike11软件包由水动力、对流～扩散、水质、降雨～径流、洪水预报等模块组成，核心模块为水动力模块。Mike11水动力模块采用6点Abbott～Ionescu有限差分格式对圣维南方程组求解。

一、圣维南方程组

1、基本要素与假设条件

Mike11模型基于以下三个要素：反映有关物理定律的微分方程组；对微分方程组进行线性化的有限差分格式；求解线性方程组的算法。并基于以下几个假定：流体为不可压缩、均质流体；一维流态；坡降小、纵向断面变化幅度小；符合静水压力假设。

2、圣维南方程组

$\left\{\begin{array}{l} \frac{\delta Q}{\delta x}+\frac{\delta A}{\delta t}=q \\ \frac{\delta Q}{\delta t}+\frac{\delta\left(\alpha \frac{Q^{2}}{A}\right)}{\delta x}+g A \frac{\delta h}{\delta x}+\frac{g Q|Q|}{C^{2} A R}=0 \end{array}\right.$
式中：Q为流量，m³/s；q为侧向入流，m³/s；A为过水面积，m²；h为水位，m；R为水力半径，m；C为谢才系数；a为动量修正系数。

3、方程离散

圣维南方程中的连续性方程和动量方程通过有限差分法进行离散，计算网格由流量点和水位点组成，其中流量点和水位点在同一时间步长下分别进行计算，见图。计算网格由模型自动生成，水位点是横断面所在的位置，相邻水位点之间的距离可能不同，流量点位于两个相邻的水位点之间。计算网格点的分布遵循以下规则：①河段上下游端点为计算水位点；②支流入流点为计算水位点；③实测断面资料点为计算水位点；④模型根据max△r值自动插入的点为计算水位点；⑤建筑物点为计算水位点；⑥两个水位点之间只存在一个计算流量点。
在这里插入图片描述

1. 连续方程

在连续方程中，引入蓄存宽度 $b_{s}$ ：
$\frac{\partial A}{\partial t}=b_{s}\frac{\partial h}{\partial t}\tag{1}$
从而连续方程转变为：
$\frac{\partial Q}{\partial x}+b_{s}\frac{\partial h}{\partial t}=q\tag{2}$
由公式可以看出仅流量Q与x有关，方程很容易得到以h点为中心的6点隐式格式见图。
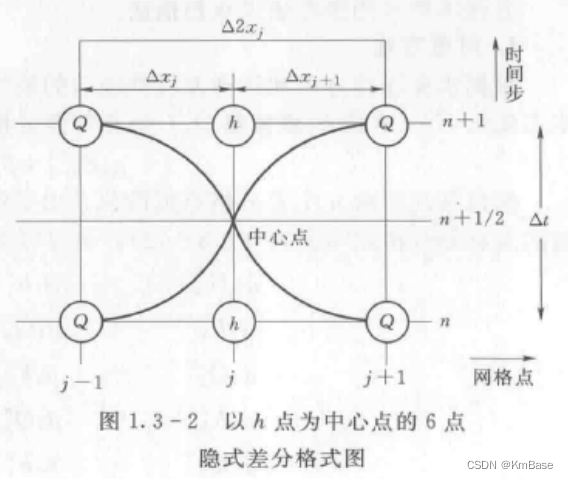
在这里插入图片描述
应用该离散格式，则连续方程变为：
$\frac{\partial Q}{\partial x} \approx \frac{\frac{Q_{j+1}^{n+1}+Q_{J+1}^{n}}{2}-\frac{Q_{j-1}^{n+1}+Q_{j-1}^{n}}{2}}{\Delta 2 x_{j}}\tag{3}$ $\frac{\partial h}{\partial t} \approx \frac{h_{j}^{n+1}-h_{j}^{n}}{\Delta t}\tag{4}$ $b_{s} \approx\frac{A_{e, j}+A_{e, j+1}}{\Delta 2 x_{j}}\tag{5}$ 式中: $A_{e, j}$ 为网格点 j-1 与 j 之间的水面面积； $A_{o, j+1}$ 为网格点 j 与 j+1 之间的水面面积； $\Delta 2 x_{j}$ 为网格点 j-1 与 j+1 之间的距离。
将式(3)、式(4)代入方程(2) 变为：
$\frac {\frac{Q_ {j+1}^ {n+1}+Q_ {j+1}^ {n}}{2}-\frac {Q_ {j+1}^ {n+1}+Q_ {j-1}^ {n}}{2}}{\triangle 2x}+b_ {s} \frac {(h_ {j}^ {n+1}-h_{j}^ {n})}{\triangle t} =q_{j}$
该方程可以简化为：
$\alpha_{j}Q_{j-1}^{n+1}+\beta_{j}h_{j}^{n+1}+\gamma_{j}Q_{j+1}^{n+1}=\delta_{j}\tag{6}$ 式中：a、β、γ为b和δ的函数，其值决定于h点在时间n处及Q点在时间n+1/2处的值。

2. 动量方程

动量方程集中在流量点，其网格形式为以Q点为中心点的差分格式见图3。
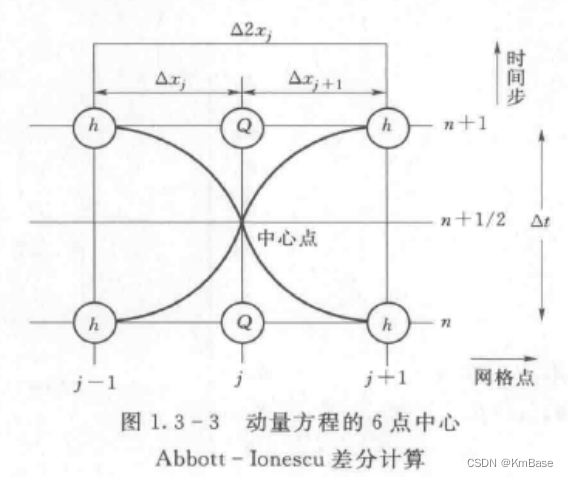
在这里插入图片描述
依据6点中心Abbott - Ionescu差分法，动量方程可以表示如下：
$\frac{\partial Q}{\partial t}\approx \frac{Q_{j}^{n+1}-Q_{j}^{n}}{\triangle t}\tag{7}$ $\frac {\partial (\alpha \frac {Q^2}{A})}{\partial x}\approx \frac{[\alpha \frac{Q^2}{A}]_{j+1}^{n+1/2}-[\alpha \frac{Q^2}{A}]_{j-1}^{n+1/2}}{\triangle 2xi}\tag{8}$ $\frac {\partial h}{\partial x}=\frac{\frac{h_{j+1}^{n+1}+h_{j+1}^{n}}{2}-\frac{h_{j-1}^{n+1}+h_{j-1}^{n}}{2}}{\triangle 2x_{j}}\tag{9}$
对公式(8)中的二次项，引入以下公式：
$Q^2\approx \theta Q_{j}^{n+1}Q_{j}^{n}-(\theta -1)Q_{j}^{n}Q_{j}^{n}\tag{10}$ 式中： θ 角的值通过HD参数文件“默认值”中的“THETA”系数来给定，默认值为1。
由上，动量方程可以表达为：
$\alpha _{j}h_{j-1}^{n+1}+\beta _{j}Q_{j}^{n+1}+\gamma _{j}h_{j+1}^{n+1}=\delta _{j}\tag{11}$ 其中 $\alpha _j=f(A)$
$\beta _j=f(Q_{j}^{n},\Delta t,\Delta x,C,A,R)$ $\gamma _j=f(A)$ $\delta _j=f(A,\Delta x,\Delta t,\alpha,q,v,\theta,h _{j-1}^{n},Q _{j-1}^{n+1/2},Q _{j}^{n},h _{j+1}^{n},Q _{j+1}^{n+1/2})$
在默认的条件下，软件在一个时间步长里用两次迭代来对这些方程进行求解。初次迭代起始于第一个时间步长，第二次迭代采用第一次计算值的中心差值来进行计算。迭代次数可以通过NoITER系数来进行修改。