【数据结构】题解：二叉树的非递归实现

文章目录

【数据结构】题解：二叉树的非递归实现
- 一、问题描述
- 二、递归实现
- 三、非递归实现
- - 3.1 前序遍历
  - 3.2 中序遍历
  - 3.3 后序遍历

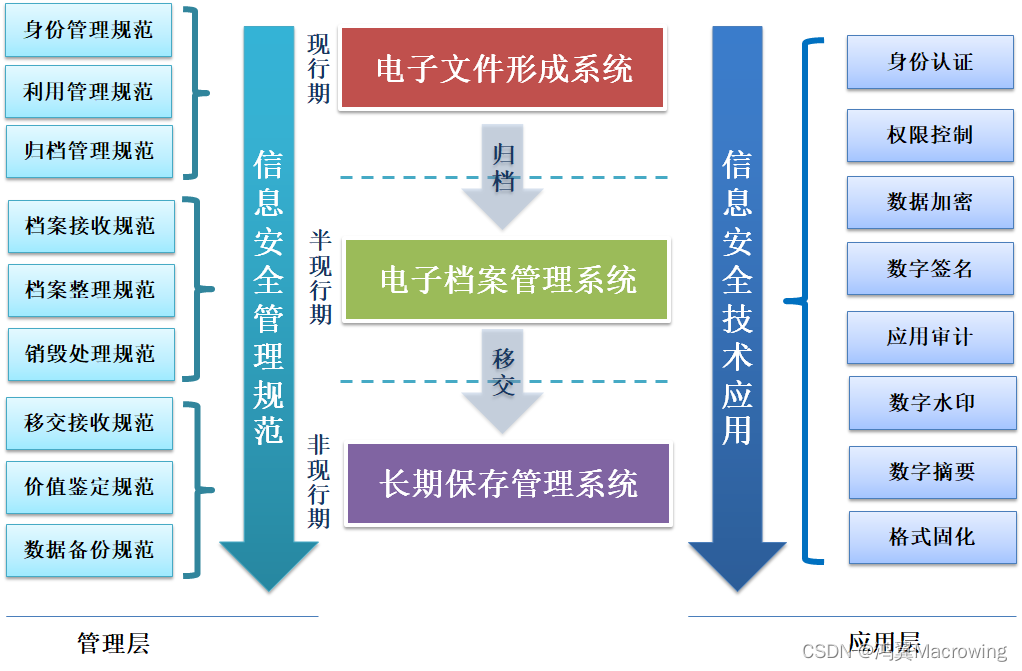
一、问题描述

二叉树的前序遍历，非递归迭代实现，二叉树的前序遍历
二叉树中序遍历，非递归迭代实现，二叉树的中序遍历
二叉树的后序遍历，非递归迭代实现，二叉树的后序遍历

前、中、后序遍历

前中后序指的是对于根访问的顺序，而对于左右子树的顺序，是左子树优先于右子树，因此对其中的总结如下：

前序遍历(Preorder Traversal 亦称先序遍历)：访问根结点的操作发生在遍历其左右子树之前
中序遍历(Inorder Traversal)：访问根结点的操作发生在遍历其左右子树之中（间）
后序遍历(Postorder Traversal)：访问根结点的操作发生在遍历其左右子树之后

如下图所示，我们对其前中后序排列进行举例：

二、递归实现

在了解非递归实现前，需要先掌握递归的实现思路，考虑如何转换为子问题的。

而对于通过前中后序遍历的实现，可以利用树的结构来实现，以前序遍历举例，先访问根，再访问左右子树，而对于左右子树而言，也是同样的思路，因此我们可以将其进行分治，使用递归实现，而递归结束的标志是没有节点在继续访问，因此当下一个子树为空时，就不再进行访问，对于代码的实现如下：

void PreOrder(BinaryTreeNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	// do something
	printf("%d ", root->val);
	PreOrder(root->left);
	PreOrder(root->right);
	return;
}

void InOrder(BinaryTreeNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	// do something
	printf("%d ", root->val);
	InOrder(root->right);
	return;
}

void PostOrder(BinaryTreeNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	// do something
	printf("%d ", root->val);
	return;
}

三、非递归实现

3.1 前序遍历

在递归实现的过程中，可以发现其子问题的解决是，将其转换为对于子树的访问，并设置了对应的终止条件。根据前序遍历的特性，可以设置一个树的访问规则，通过循环来完成树的先序遍历。

访问根节点，将其入栅，用于访问完左子树后，进行右子树的访问，再访问左路节点
出栈，通过栈中元素左路节点访问右子树

在这里插入图片描述

按照以上思路可以进行代码的编写，过程如下：

创建一个容器来存放遍历后的数据，创建一个栈进行访问需要访问右子树的左节点储存
通过循环进行每棵树的子问题进行，循环中的内容为各个树的访问规则，即访问当前节点，并不断的访问左节点，直到没有左节点，再通过栈顶元素，进行其右节点的访问。
其结束条件相对于树而言是存在该树即不可为空，对于访问过程而言，当还有需要访问的树时循环继续，即栈不为空

代码示例如下：

vector<int> preorderTraversal(TreeNode* root) {
    vector<int> ret;
    TreeNode* cur = root;
    stack<TreeNode*> st;
    // 循环一次表示一次迭代，表示访问一棵树
    while(cur || !st.empty()){
        // 访问根节点并入栈，再访问左路节点
        while(cur){
            ret.push_back(cur->val);
            st.push(cur);
            cur = cur->left;
        }
		// 从栈顶中访问需要被访问右子树的节点
        TreeNode* top = st.top();
        st.pop();
        cur = top->right;
    }
    return ret;
}

3.2 中序遍历

该遍历过程与前序遍历类似，主要差别为访问时机不同，前序遍历是先访问根的，因此当到达某个节点时，直接访问即可。而中序遍历时访问完左节点后，再访问根节点，实际也是访问右子树前进行访问根节点，因此只需对代码访问根节点的实际，进行修改即可，代码示例如下：

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> ret;
    TreeNode* cur = root;
    stack<TreeNode*> st;
    while(cur || !st.empty()){
        while(cur){
            st.push(cur);
            cur = cur->left;
        }
        
        TreeNode* top = st.top();
        ret.push_back(top->val);
        st.pop();
        cur = top->right;
    }
    return ret;
}

3.3 后序遍历

对于后序遍历的访问过程则是更为复杂，通过栈来对树进行遍历，其困难出现在，当访问右节点前会对根进行访问一次，此时时不如栈的，再对右节点访问后，由于其根没有如栈，还会对根进行访问一次，此时需要将其入栈。经过这两次访问过程，比较难的确定是何时入栈。图示如下：

为了解决该问题，可以引入多一个指针，表示上一个访问的节点，当根节点的右节点为指针指向的结点时，进行入栈，否则不入栈，图示如下：
在这里插入图片描述

代码示例如下：

vector<int> postorderTraversal(TreeNode* root) {
    vector<int> ret;
    TreeNode* cur = root;
    TreeNode* prev = nullptr;
    stack<TreeNode*> st;
    while(cur || !st.empty()){
        while(cur){
            st.push(cur);
            cur = cur->left;
        }

        TreeNode* top = st.top();
        // 右子树为空或者上一访问节点为根节点的右节点
        if(top->right == nullptr || top->right == prev){
            // 访问该节点
            ret.push_back(top->val);
            // 修改前驱指针
            prev = top;
            st.pop();
            // 不再访问右子树
        }
        else{
            // 访问右子树
            cur = top->right;
        }
    }
    return ret;
}