1 前言
本文主要讲解层次分析法(AHP)的python实现,后续会跟进实例分析
2 代码实现
导入包
import numpy as np
2.1 构造判断矩阵
判断矩阵一般采用专家意见法,也就是德尔菲法。但是比赛的时候也没有什么专家,大家自己看着整就行,当然有很多文章对层次分析法进行了改进,大家可以自行滴进行参考。

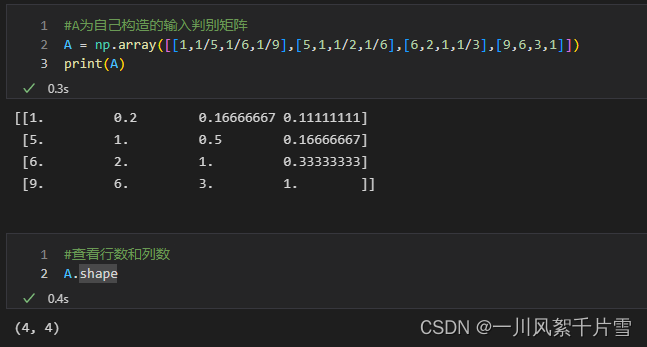
本文定义一个4*4的判断矩阵,也就是有4个指标
A = np.array([[1,1/5,1/6,1/9],[5,1,1/2,1/6],[6,2,1,1/3],[9,6,3,1]])
print(A)
查看矩阵的行列数
#查看行数和列数
A.shape
2.2 求特征值和特征向量
求解特征值和特征向量的方法主要参考了下方的博客
#求特征值和特征向量
'''
https://blog.csdn.net/Strive_For_Future/article/details/109631691
w,v = numpy.linalg.eig(a) 计算方形矩阵a的特征值和右特征向量
a : 待求特征值和特征向量的方阵。
w: 多个特征值组成的一个矢量。备注:多个特征值并没有按特定的次序排列。特征值中可能包含复数。
v: 多个特征向量组成的一个矩阵。每一个特征向量都被归一化了。第i列的特征向量v[:,i]对应第i个特征值w[i]。
'''
V,D = np.linalg.eig(A) # 求特征值和特征向量
print('特征值:')
print(V)
print('特征向量:')
print(D)
输出最大特征值和最大特征向量,也就是我们需要的
#最大特征值
tzz = np.max(V)
print('最大特征值为:\n', tzz)
#最大特征向量
k=[i for i in range(len(V)) if V[i] == np.max(V)]
tzx = -D[:,k]
print('最大特征值向量为:\n',tzx)
得到权重Q,这个Q也就是我们最终需要的权重矩阵,也就是每个指标的权重
# 赋权重
n = A.shape[1]
quan=np.zeros((n,1))
for i in range(0,n):
quan[i]=tzx[i]/np.sum(tzx)
Q=quan
print(Q)

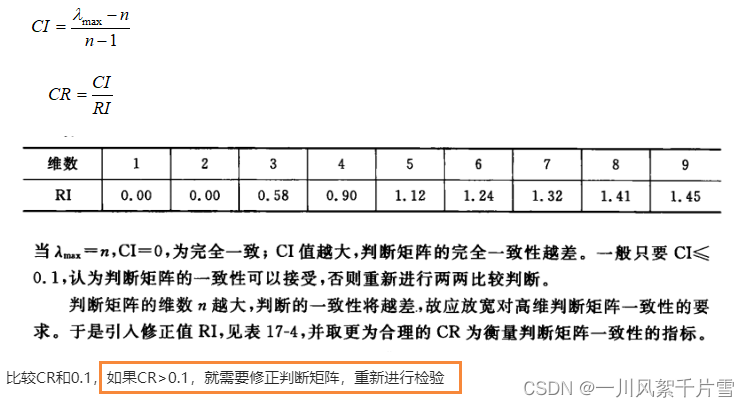
2.3 一致性检验
这个就是检验一下,咱们自己的判断矩阵是否合理。一致性检验通过了就是能用,不通过就是我们在进行专家打分的时候有问题,就得修正判断矩阵。
#一致性检验
CI=(tzz-n)/(n-1)
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59]
#判断是否通过一致性检验
CR=CI/RI[n-1]
if CR>=0.1:
print('没有通过一致性检验, 判断矩阵需要进行修正\n')
else:
print('通过一致性检验\n')
3 实例分析
假设有两个对象,分数分别为:
对象A: [8 7 6 8]
对象B: [7 8 8 7]
# 假设有两个目标
p = np.mat('8 7 6 8;7 8 8 7') #每一行代表一个对象的指标评分
print(p)
然后使用上方得到的权重Q,对这两个对象进行打分
#显示出所有评分对象的评分值
score=p*Q
for i in range(len(score)):
print('object_score {}:'.format(i),float(score[i]))
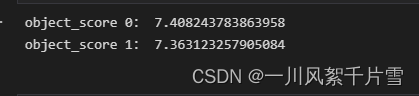
可以看到A比B的得分要高,大家可以尝试一下定义不同的判断矩阵,查看打分的变化情况。