2019-arXiv-Edge Contraction Pooling for Graph Neural

Paper: https://arxiv.org/abs/1905.10990
Code: https://github.com/pyg-team/pytorch_geometric/tree/master/benchmark/kernel
图神经网络的边缘收缩池化
池化层可以使GNN对抽象的节点组而不是单个节点进行推理。为了缩小这一差距,作者提出了一个依赖于边缘收缩概念的图池层:EdgePool 学习局部和稀疏的硬池转换。实验表明,EdgePool优于其他池化方法,可以很容易地集成到大多数GNN模型中,并提高了节点和图分类的性能。
边缘池层的主要优点是:
- EdgePool的性能优于其他池化方法。
- EdgePool可以集成到现有的图形分类架构中。
- EdgePool可用于节点分类并提高性能。
模型
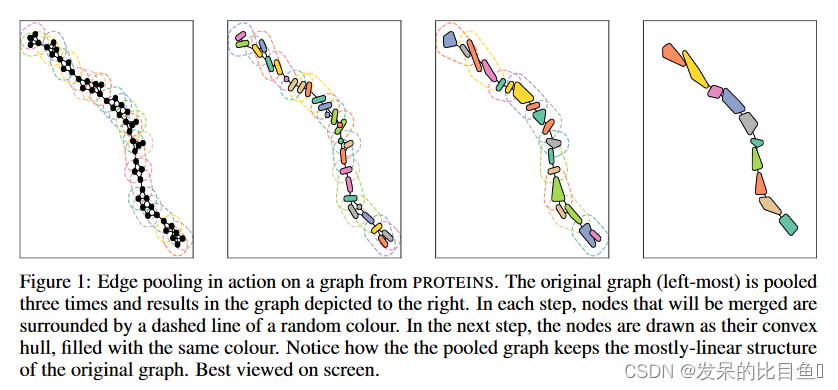
下图表示作用在蛋白质图中的基于边收缩的池化机制。原始图(最左边)被池化了三次,结果为最右侧的图。在每个步骤中,将要合并的节点周围都有一条随机颜色的虚线。在下一步中,将节点绘制为它们的凸形,填充相同的颜色。
图基础: 图 G = ( V , E ) G = (V, E) G=(V,E),其中每个 v v v 节点都有 f f f 特征 V ∈ R v × f V \in R^{v×f} V∈Rv×f 。边表示为没有权重或特征的有向节点对。
边缘收缩
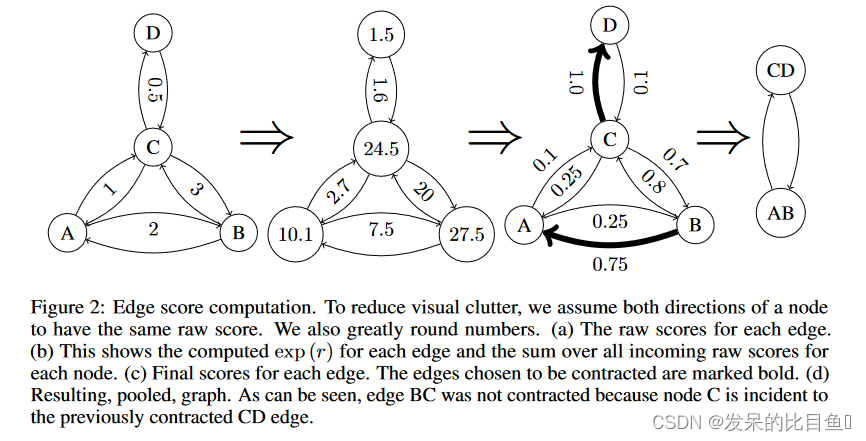
池化操作基于边缘收缩。收缩边 e = { v i , v j } e = \{v_i, v_j\} e={vi,vj} 引入新节点 v e v_e ve 和新边,使得 v e v_e ve 与所有节点 v i v_i vi 相邻或 v j v_j vj 已经相邻。 v i v_i vi、 v j v_j vj 及其所有边将从图形中删除。由于边收缩是可交换的,也可以定义边集收缩。通过构造集合,使得没有两条边入射到同一个节点,可以简单地多次应用单边收缩的朴素概念。
通过合并其节点来选择单个边缘进行收缩。然后,此新节点将连接到合并节点已连接到的所有节点。多次重复此过程,注意不要将新合并的节点包含在其中。
选择边
EdgePool对每条边设计了一个可学习的分数,然后根据边的分数来选择保留还是丢弃所连的节点。边的分数通过对节点特征的线性变换来计算,节点
x
i
x_{i}
xi和节点
x
j
x_{j}
xj所连的边的分数
r
i
j
r_{i j}
rij, 如果图中的边还有特征
e
i
j
e_{ij}
eij,那么也可以同时将边的特征也融入其中,也就是做了一个简单的拼接:

虽然每个节点只沿着一条边进行收缩,但是每个节点可能有多条可选的边,可将节点邻接的边的分数归一化,使得不同边之间的分数便于相互比较:

计算新节点特征
为了使梯度流入分数,我们使用门控并将组合的节点特征乘以边缘分数:

计算性能
EdgePool 是本地独立的:只要两个节点 n i n_i ni 和 n j n_j nj 及其邻居的节点分数不改变(通过更改感受野内的节点),边缘 e i j e_{ij} eij 的选择就不会改变。因此,不必一次为整个图形计算边缘池。如果图形发生更改,则只需要更新已更改区域的本地池化。
集成边缘要素
更新边缘池以考虑边缘
e
i
j
e_{ij}
eij 的边缘特征。为此将它们包含在原始分数计算中(公式(1))。最简单的方法是将它们连接起来:
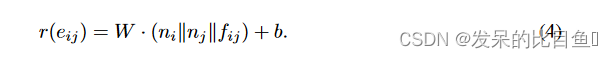
反池化EdgePool
对于节点分类来说,还是需要一个解池化的操作。对于解池化的操作,只需要对新的节点特征进行还原即可:

实验
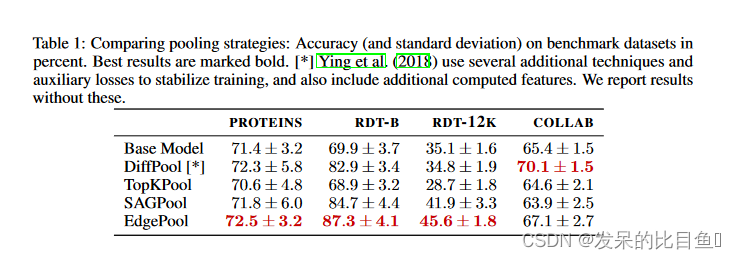
Table1 中是与其他不同的池化操作的对比,为了验证EdgePool的性能是否优于其他池化方法。
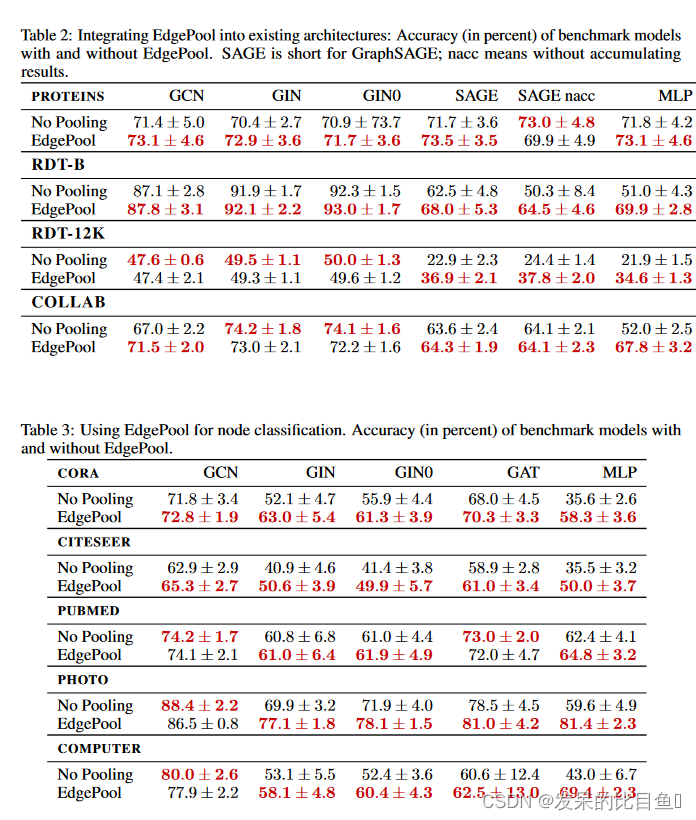
Table2 是将edgepool技术和其他GNN框架融合之后的效果(图分类),为了验证EdgePool是否可以集成到现有的GNN架构中。
Table3 是与其他GNN模型在节点分类任务上结合的效果。