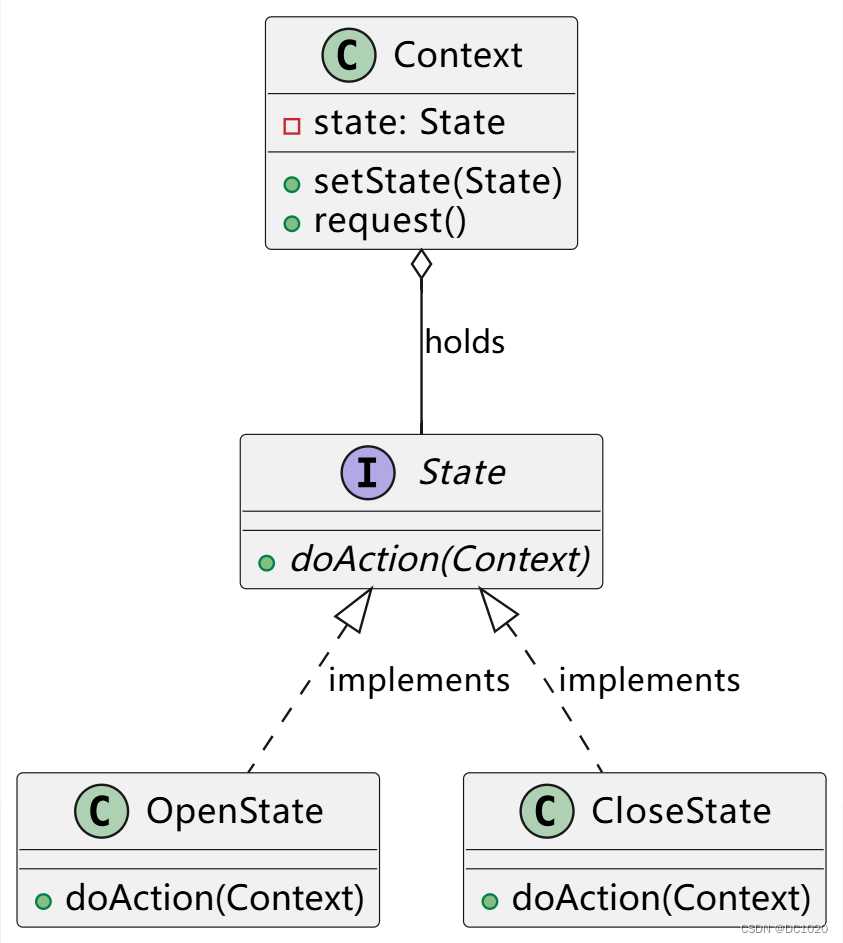
目录

Regression for Dummies

Conditionally Random Experiments

Dummy Variables

---

Regression for Dummies

回归和正交化固然很好，但归根结底，你必须做出独立性假设。你必须假设，在考虑到某些协变量的情况下，干预看起来与随机分配一样好。这可能相当困难。很难知道模型中是否包含了所有的混杂因素。因此，尽可能推动随机实验是非常有意义的。例如，在银行业的例子中，如果信用额度是随机的就好了，因为这样就可以很直接地估算出信用额度对违约率和客户消费的影响。问题是，这个实验的成本将高得惊人。你将会给风险极高的客户提供随机信用额度，而这些客户很可能会违约并造成巨大损失。

Conditionally Random Experiments

解决这一难题的方法并不是理想的随机对照试验，但却是最理想的方法：分层或有条件随机试验。在这种实验中，实验线不是完全随机的，而是从相同的概率分布中抽取的，因此您需要创建多个局部实验，根据客户的协变量从不同的分布中抽取样本。例如，您知道变量 credit_score1 是客户风险的代理变量。因此，您可以用它来创建风险较高或较低的客户群体，将他们划分为信用分数 1 相似的桶。然后，对于高风险组（信用分数低），您可以从平均分较低的分布中随机抽取信用额度；对于低风险客户（信用分数高），您可以从平均分较高的分布中随机抽取信用额度：

 risk_data_rnd = pd.read_csv("./data/risk_data_rnd.csv")
 risk_data_rnd.head()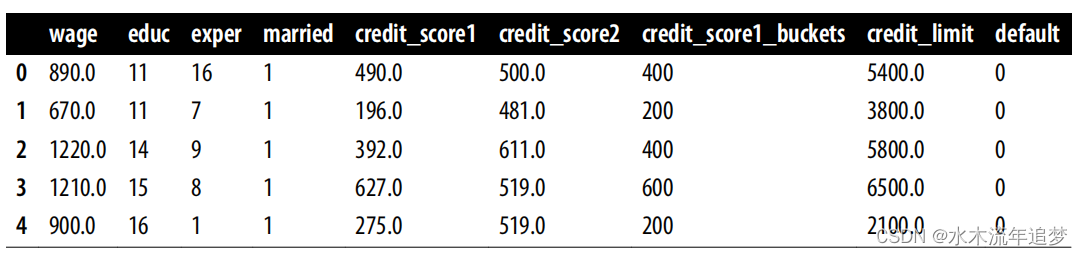

绘制按credit_score1_buckets划分的信用额度直方图，可以看到各行的取样分布不同。得分较高的组别--低风险客户--的直方图向左倾斜，线条较长。风险较高的客户组--低分--的贷款额度分布图向右倾斜，贷款额度较低。这种实验探索的信贷额度与最佳额度相差不大，从而降低了测试成本，使其更易于管理：

这并不意味着条件随机实验比完全随机实验更好。出于这个原因，如果您选择条件随机实验，无论出于什么原因，都要尽量使其接近完全随机实验。这意味着

• - 组数越少，处理条件随机测试就越容易。在本例中，您只有 5 个组，因为您把 credit_score1 分成了 200 个桶，分数从 0 到 1,000。将不同的组与不同的干预分布结合起来会增加复杂性，因此坚持少分组是个好主意。
• - 各组间干预分布的重叠越大，你的实验就越轻松。这与阳性假设有关。在这个例子中，如果高风险组获得高线的概率为零，那么您就必须依靠危险的推断才能知道如果他们获得高线会发生什么。

如果把这两条经验法则调到最大值，就会得到一个完全随机的实验，这意味着这两条经验法则都需要权衡：组数越少，重叠度越高，实验就越容易读取，但成本也越高，反之亦然。

Dummy Variables

条件随机实验的好处在于，条件独立性假设更加可信，因为你知道在你选择的分类变量下，各条线是随机分配的。其缺点是，简单地将结果与被处理者进行回归，会产生有偏差的估计值。例如，以下是在不包含混杂因素的情况下估计模型的结果：

 model = smf.ols("default ~ credit_limit", data=risk_data_rnd).fit()
 model.summary().tables[1]

如图所示，因果参数 β1 的估计值为负值，这在这里是没有意义的。较高的信用额度可能并不会降低客户的风险。实际情况是，在这个数据中，由于实验的设计方式，风险较低的客户--credit_score1 高的客户--平均获得了更高的额度。

为了对此进行调整，需要在模型中加入随机分配干预的组别。在这种情况下，需要credit_score1_buckets. 进行控制。尽管该组用数字表示，但它实际上是一个分类变量：它代表一个组。因此，控制组本身的方法是创建哑变量。虚拟变量是一个群体的二进制列。如果客户属于该组，则为 1，否则为 0。由于一个客户只能来自一个组，因此最多只有一列虚拟变量为 1，其他列均为 0。如果您有机器学习背景，您可能会知道这是one-hot。它们完全是一回事。

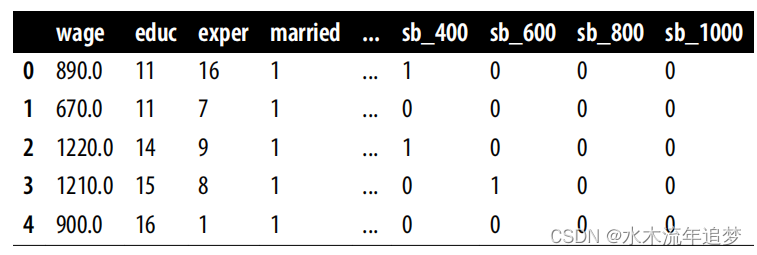
在 pandas 中，你可以使用 pd.get_dummies 函数来创建哑列。在这里，我传递了表示组的列 credit_score1_buckets，并表示我想要创建后缀为 sb（表示分数桶）的哑列。此外，我还删除了第一个虚拟列，即 0 到 200 分桶的虚拟列。这是因为其中一列是多余的。如果我知道所有其他列都是 0，那么我放弃的那一列 一定是 1：

 risk_data_dummies = (
risk_data_rnd
 .join(pd.get_dummies(risk_data_rnd["credit_score1_buckets"],
 prefix="sb",
 drop_first=True))
)

一旦您有了虚拟列，您就可以将它们添加到您的模型中，并再次估计β1：

现在，你会得到一个更合理的估计，这至少是积极的，这表明更多的信用额度会增加违约风险。

 model = smf.ols(
 "default ~ credit_limit + sb_200+sb_400+sb_600+sb_800+sb_1000",
 data=risk_data_dummies
 ).fit()
 model.summary().tables[1]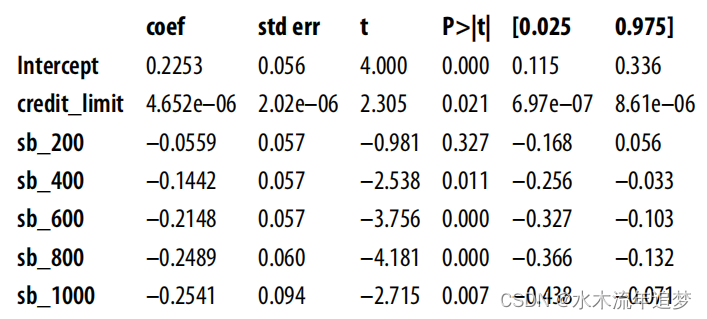

 model = smf.ols("default ~ credit_limit + C(credit_score1_buckets)",
 data=risk_data_rnd).fit()
 model.summary().tables[1]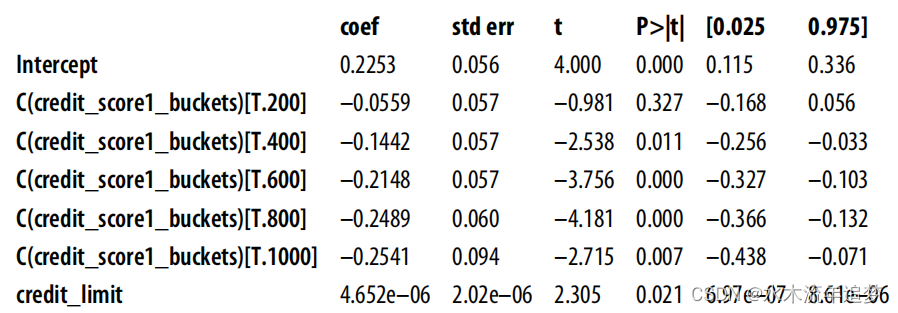

最后，这里只有一个斜率参数。添加虚拟变量来控制混杂因素后，每个组都有一个截距，但所有组的斜率都是一样的。我们很快就会讨论这个问题，但这个斜率将是各组回归的方差加权平均值。如果绘制每个组的模型预测图，您可以清楚地看到每个组只有一条线，但所有组的斜率相同：