一、Seq2seq的局限性

Seq2seq（序列到序列）模型我们在前面讲了它的原理，是一种广泛用于处理序列转换任务的深度学习架构，特别是在机器翻译、文本摘要、对话生成等应用中。然而，尽管seq2seq模型在某些领域取得了显著的成果，它仍然存在一些局限性，以下是对您提到的两个局限性的更正式和详细的描述：

1. 信息遗忘问题（Information Forgetting）：

   • 在seq2seq模型中，编码器（Encoder）负责将输入序列转换为固定大小的上下文向量，而解码器（Decoder）则基于这个上下文向量生成输出序列。对于循环神经网络（RNN）及其变体，如长短时记忆网络（LSTM）和门控循环单元（GRU），它们在处理长序列时可能面临信息遗忘的问题。
   • 随着序列长度的增加，这些模型可能会逐渐丢失早期输入信息，导致在生成输出序列时无法充分利用所有相关信息。这种信息丢失可能会降低模型的性能，特别是在需要长期依赖关系的复杂任务中。

2. 信息不对齐问题（Information Misalignment）：

   • 在seq2seq模型的解码阶段，模型需要生成与输入序列相对应的输出序列。然而，模型在处理输入序列时，可能会对所有单词给予相同的关注度，而不是根据它们对输出序列的相关性进行加权。
   • 这种信息不对齐可能导致模型无法准确地捕捉输入序列中的关键信息，从而影响输出序列的质量和相关性。例如，在机器翻译任务中，某些词汇或短语可能对翻译的整体意义至关重要，但模型可能无法识别并给予适当的重视。

为了克服这些局限性，我们看一下Attention机制是如何做的。

二、Attention介绍

Attention机制是一项先进技术，用于增强基于循环神经网络（RNN）、长短时记忆网络（LSTM）和门控循环单元（GRU）的编码器-解码器模型性能。它通常被称作Attention Mechanism，在深度学习领域非常流行，广泛应用于机器翻译、语音识别、图像标注等多个领域。

1. Attention机制的作用与流行原因：
   通过为序列中每个元素分配不同权重，Attention机制增强了模型的信息区分和识别能力。这种权重分配让模型更灵活地学习，尤其是在处理句子中每个词时，能根据其对翻译或识别结果的重要性进行调整。Attention机制还提供对齐关系，帮助解释输入输出序列间的对应关系，揭示模型学习的知识，为理解深度学习模型内部机制提供途径。
2. Attention机制的历史与发展：
   Attention机制的概念最早在20世纪90年代提出，初应用于计算机视觉领域，后在自然语言处理领域迅速发展，并近期在计算机视觉领域再获广泛关注。
3. Attention机制与人类视觉注意力的关系：
   Attention机制的灵感来自人类视觉注意力机制，一种仿生学应用。人类视觉系统能快速扫描场景，识别重点关注区域，集中注意力资源获取目标细节信息，忽略无关信息。这是人类长期进化中形成的生存策略，提高了视觉信息处理效率和准确性。
4. 人类视觉注意力机制的特点：
   人类视觉注意力机制利用有限注意力资源从大量信息中快速筛选高价值信息。这使人类能在复杂环境中快速识别响应重要视觉刺激，是进化中形成的高效信息处理方式。

三、原理解析

在传统的seq2seq中，解码器对于编码器的输入信息全部来自于H

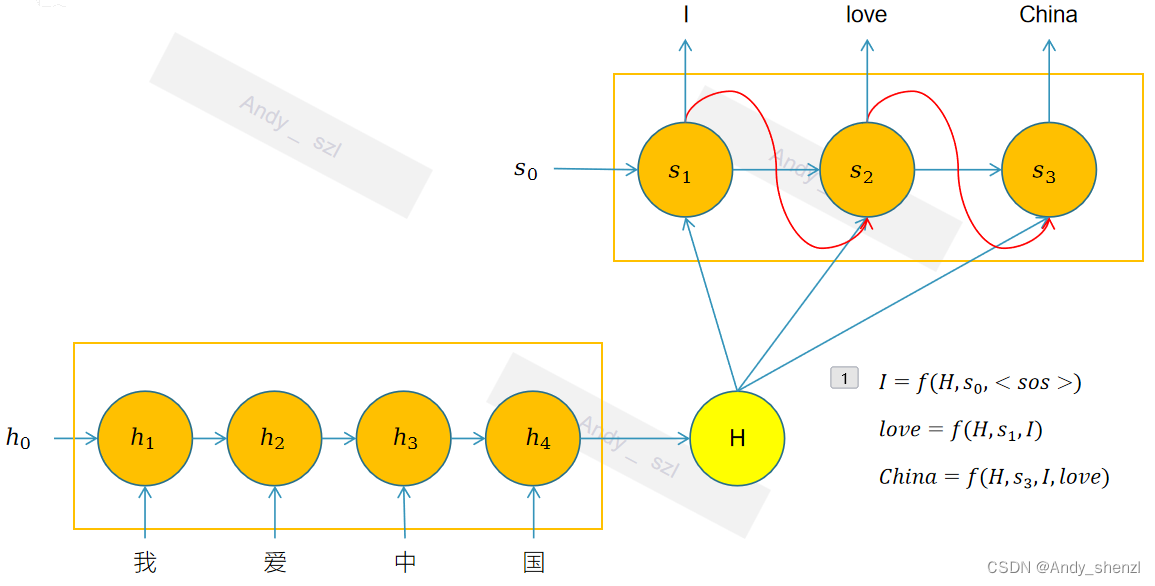
Attention模型的一个关键特点是它对传统的编码器-解码器（Encoder-Decoder）架构进行了改进，使得解码器（Decoder）在生成每个新的输出单词时，不是依赖于整个输入序列编码成的固定长度的中间语义向量 H，而是能够动态地计算并关注输入序列中与当前生成的单词最相关的部分，如下图。

解码器的输入过程就变成了：
$I=f(c_1,<sos>)$
$love=f(c_2,I)$
$China=f(c_3,I,love)$

整个Attention机制的重点是查看$c_1,c_2,c_3$是如何计算的

3.1 注意力分数

我们以$C_1$为例来说明

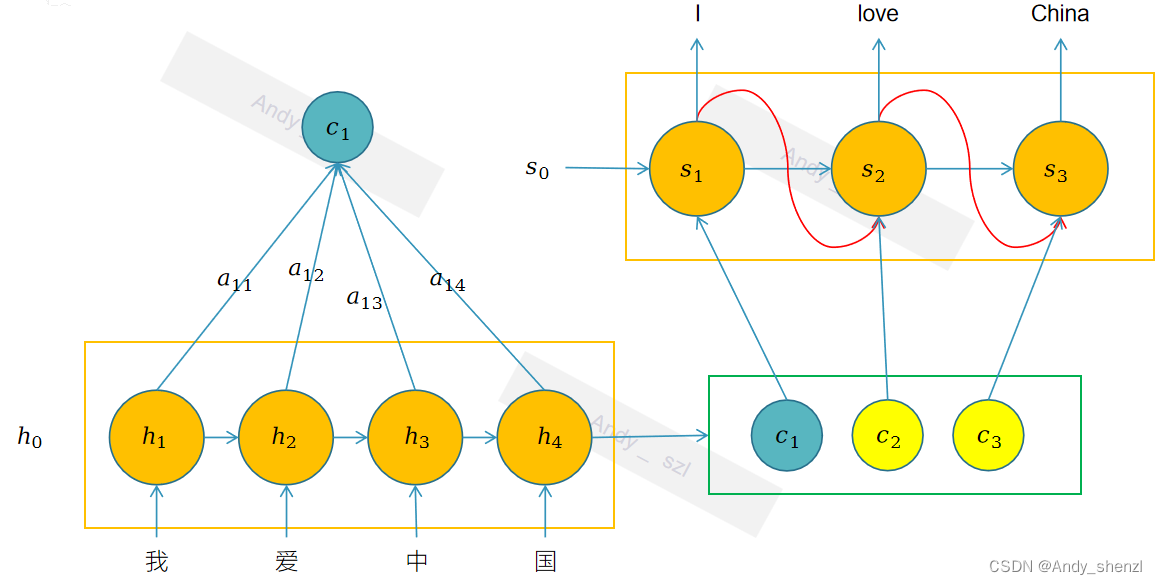
图片中的是C1注意力权重公式的示例。根据图片中的内容，我们可以看到：

1. ${\mathbf{h}}_1$，${\mathbf{h}}_2$，${\mathbf{h}}_3$，${\mathbf{h}}_4$是编码器每个时间状态的隐藏层信息；

2. ${\alpha }_{ij}$ 是输入序列中第 $j$ 个词对解码时间步$i$的注意力权重，比如${\alpha }_{12}$是编码器第2个时刻${\mathbf{h}}_2$ 对于解码器第1个时刻的注意力权重；

3. ${\mathbf{C}}_1={\alpha }_{11}\ast {\mathbf{h}}_1+{\alpha }_{12}\ast {\mathbf{h}}_2+{\alpha }_{13}\ast {\mathbf{h}}_3+{\alpha }_{14}\ast {\mathbf{h}}_4$，${\alpha }_{ij}$可以看成是解码器在生成第一个单词I时，和编码器中每个时刻生成的隐藏层${\mathbf{h}}_j$的相关性；因为${\mathbf{h}}_j$是每个时刻生成的隐藏状态，其实是包含了当前时间点输入的主要内容；所以我们可以理解为这里需要计算的是单词I和“我”，“爱“，”中“，”国”每个时刻输入内容的相关性。当然这里的${\mathbf{h}}_j$其实是包含了部分上文信息的（在原始的论文中采用的是双向的RNN，也就是包含上下文信息的）。所以在生成单词I时，理论上与“我”的相关性最大，与其他的汉字`“爱“，”中“，”国”``的相关性较小。在其他的时间节点类似。

4. 公式信息：注意力机制的计算公式，对于解码步骤 ( i ) 的上下文向量 ${\mathbf{C}}_i$，它的计算方式是：
   ${\mathbf{C}}_i={\sum }_{j=1}^n{\alpha }_{ij}{\mathbf{h}}_j$

   其中：

   • ${\alpha }_{ij}$ 是输入序列中第 $j$ 个词对解码步骤$i$的注意力权重。
   • ${\mathbf{h}}_j$ 是编码器输出的第$j$ 个词的隐藏状态。
   • $n$ 是输入序列的长度。

5. 补充全部公式：
   ${\mathbf{C}}_1={\alpha }_{11}\ast {\mathbf{h}}_1+{\alpha }_{12}\ast {\mathbf{h}}_2+{\alpha }_{13}\ast {\mathbf{h}}_3+{\alpha }_{14}\ast {\mathbf{h}}_4$
   ${\mathbf{C}}_2={\alpha }_{21}\ast {\mathbf{h}}_1+{\alpha }_{22}\ast {\mathbf{h}}_2+{\alpha }_{23}\ast {\mathbf{h}}_3+{\alpha }_{24}\ast {\mathbf{h}}_4$
   ${\mathbf{C}}_3={\alpha }_{31}\ast {\mathbf{h}}_1+{\alpha }_{32}\ast {\mathbf{h}}_2+{\alpha }_{33}\ast {\mathbf{h}}_3+{\alpha }_{34}\ast {\mathbf{h}}_4$

那么这个 ${\alpha }_{ij}$ 是怎么计算出来的呢？

3.2 注意力分数计算

还是以输出的第一个时刻为例：

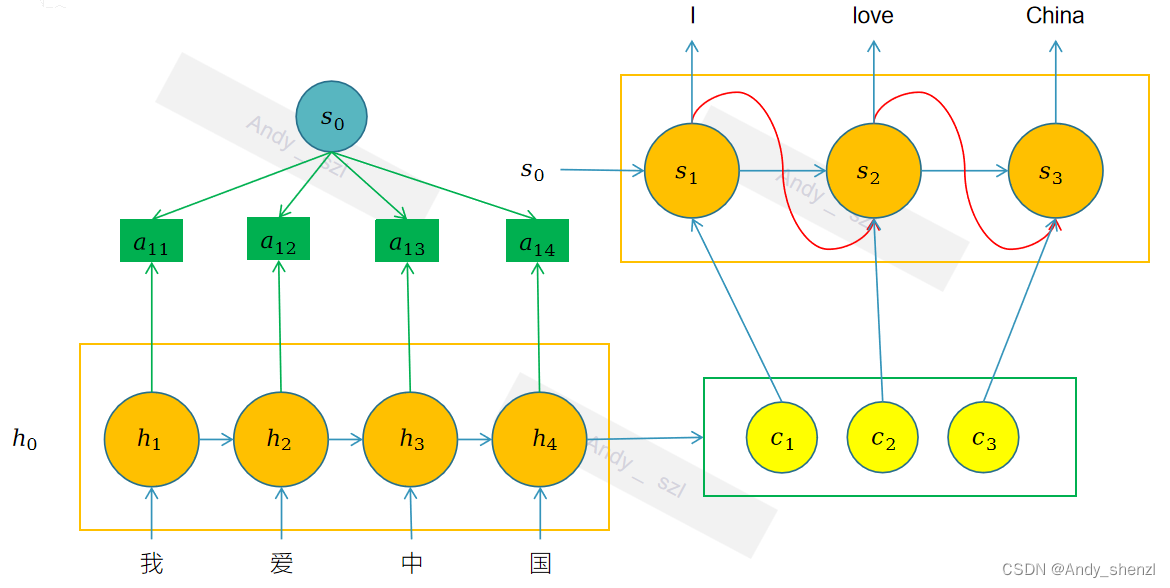
在传统seq2seq的decode中，输入有三个：encode的隐藏状态、前一个时刻的输入和前一个隐藏状态；在注意力机制中就是使用前一个时刻的隐藏状态${\mathbf{s}}_{i-1}$ 和encode中每一个时刻的隐藏状态${\mathbf{h}}_j$进行计算得到${\alpha }_{ij}$ ;

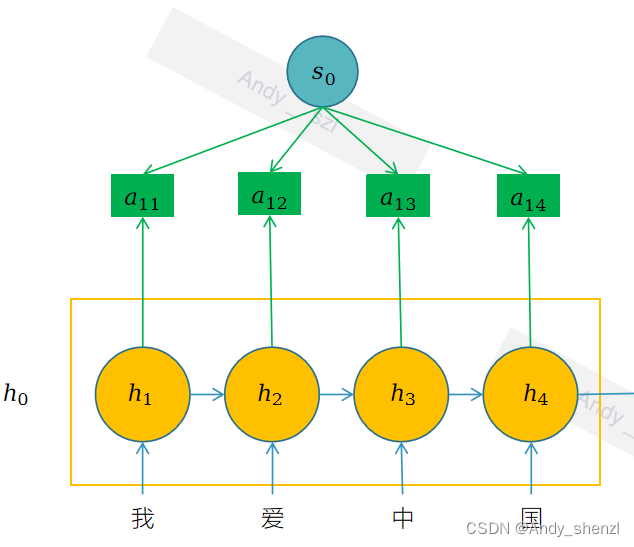
比如第一个decode中的注意力权重就是隐藏状态${\mathbf{s}}_0$与encode中每一个时刻的隐藏状态${\mathbf{h}}_j$进行计算得到${\alpha }_{1j}$。

具体的计算方法有两种：
图片中提供的信息描述了注意力机制中权重 ( \alpha_{ij} ) 的计算方法以及它在模型中的作用。以下是核心内容的整理：

• 使用神经网络计算权重：
  图片中提供的信息描述了注意力机制中匹配得分 ( e_{ij} ) 的计算方法，这是计算注意力权重 ( \alpha_{ij} ) 的基础。以下是核心内容的整理：

  1. 匹配得分$e_{ij}$ 的计算：

     • 匹配得分$e_{ij}$ 表示解码器在第 $i-1$ 步的隐状态${\mathbf{s}}_{i-1}$ 和编码器在第$j$ 步的隐向量 ${\mathbf{h}}_j$ 之间的匹配程度。

  2. 使用双曲正切函数的计算方法：

     • 匹配得分$e_{ij}$ 可以通过以下公式计算：
       $e_{ij}={\mathbf{v}}^T\tanh (W{\mathbf{s}}_{i-1}+V{\mathbf{h}}_j)$
       其中：
     • $\mathbf{v}$ 是可学习的权重向量。
     • $W$ 和$V$ 是可学习的权重矩阵。
     • $\tanh$ 是双曲正切激活函数，用于引入非线性。

  请注意，这里的${\mathbf{v}}^T$ 表示向量$\mathbf{v}$的转置。这种计算方法是一种常见的注意力机制实现，它通过神经网络的方式捕捉解码器和编码器状态之间的交互。

• 使用二次型矩阵计算权重：
  二次型矩阵计算方法是一种用于计算注意力权重 ${\alpha }_{ij}$ 的技术，通常出现在注意力机制中。这种方法的核心思想是通过一个二次型（一个向量和矩阵的乘积）来衡量解码器的前一状态${\mathbf{s}}_{i-1}$ 与编码器的每个状态 ${\mathbf{h}}_j$ 之间的关联度。下面是对这种方法的解读：
  二次型矩阵计算方法的公式如下：
  $e_{ij}={\mathbf{s}}_{i-1}^T{W}_{i-1,j}{\mathbf{h}}_j$

  其中：

  • $e_{ij}$ 是解码器在第$i-1$ 步的隐状态 ${\mathbf{s}}_{i-1}$ 和编码器在第$j$ 步的隐向量${\mathbf{h}}_j$ 之间的匹配得分。
  • ${\mathbf{s}}_{i-1}$ 是解码器在第 $i-1$ 步的隐状态，通常是一个向量。
  • $W_{i-1,j}$ 是一个可学习的权重矩阵，用于调整解码器和编码器状态之间的关系。这个矩阵可能依赖于解码器的步骤$i-1$ 和编码器的步骤 $j$。
  • ${\mathbf{h}}_j$ 是编码器在第$j$ 步的隐向量。

四、计算步骤

1. 计算匹配得分：首先，使用权重矩阵$W_{i-1,j}$ 将编码器的隐向量 ${\mathbf{h}}_j$ 转换为一个新的向量。

2. 计算匹配得分：然后，将解码器的隐状态 ${\mathbf{s}}_{i-1}$ 与转换后的编码器隐向量进行点积，得到匹配得分$e_{ij}$。

3. 计算权重：通过计算得到的匹配得分$e_{ij}$ 通常需要通过Softmax函数进行归一化，以得到最终的注意力权重 ${\alpha }_{ij}$：

   ${\alpha }_{ij}=\frac{\exp (e_{ij})}{{\sum }_{k=1}^n\exp (e_{ik})}$

   这样，每个${\alpha }_{ij}$ 都在 0 到 1 之间，并且所有${\alpha }_{ij}$ 的和为 1。