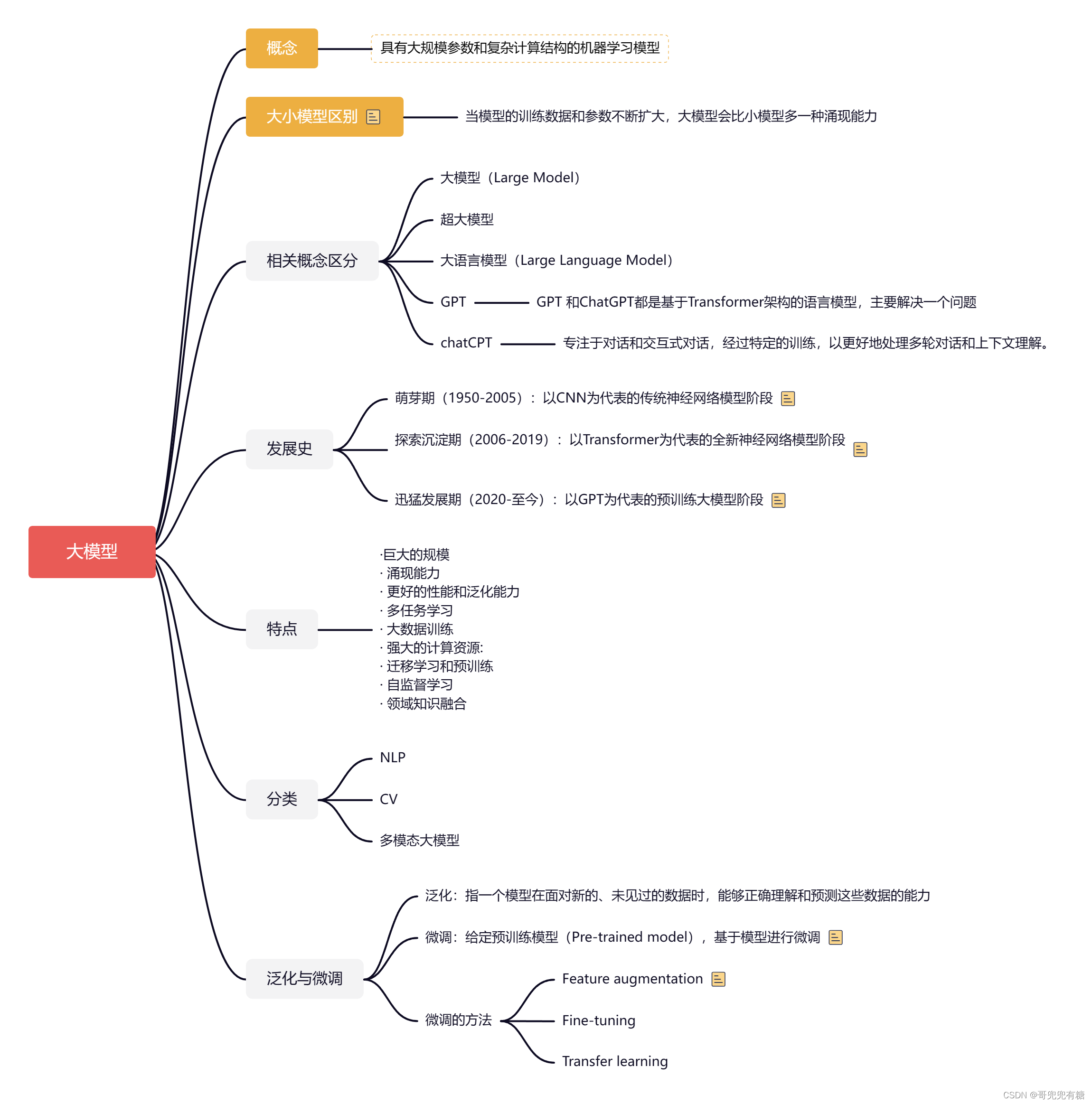
一、全连接到卷积

1、卷积具有两个原则：

        平移不变性：无论作用在哪个部分，它都要有相同的作用，而不会随着位置的改变而改变

        局部性：卷积核作用处，作用域应该是核作用点的周围一小部分而不作用于更大的部分

2、卷积是一个特殊的全连接层。

（1）对输入输出：长度变化->高宽变化；

（2）对权重：之前输入输出都是一维，权重就是二维。现在输入输出都是二维，权重就是四维了；全连接层的权重矩阵的维度可以表示为 (n,m)，其中 n 是输入神经元的数量，m 是输出神经元的数量。如果一个全连接层有 4 个输入维度和 3 个输出维度，那么它的权重矩阵的维度就是 4×3

（3）与全连接二维权重类似，只是从二维变成了四维

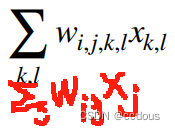
（4）把下标变一下，使得可以引出卷积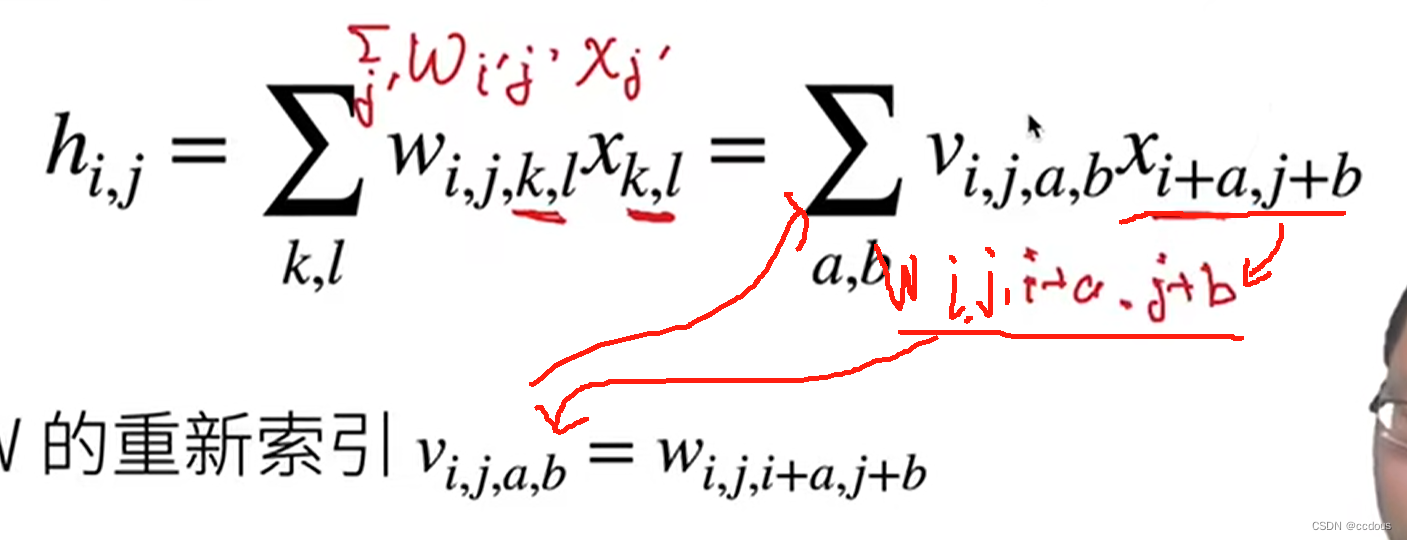

3、对应两个原则，处理上面的等式

（1）平移不变形

        i,j变的时候，不能让w跟着变，即在别的维度都是一样的权重，否则失去平移不变性

        平移不变性让我们对权重有一个限制，把ij的维度抹去，从四维变为二维

（2）局部性

4、权重是识别图片的识别器，

5、总结

（1）对全连接层使用平移不变性和局部性得到卷积层

（2）“卷积核在数值不变的情况下遍历整张图”、“卷积核不应该太大”

（3）这是卷积操作子的情况，后面会写卷积层的操作

二、卷积层

1、二维卷积层

（1）对输出Y：Kernel为2×2的矩阵，那么德尔塔就应该等于1

（2）卷积核与输入的位置无关，这叫做平移不变性；输出的一个窗口所用的只是一个2×2的矩阵，这说明了局部性

（3）w =其实就是kernel

（4）卷积核矩阵的大小，控制的是局部性；卷积为了保持局部性，不会随着输入维度的变大而使核变复杂

2、交叉相关与卷积

        只是学出来的东西是反的，其他没有区别

3、一维与三维：一维交叉相关主要处理文本语言时序序列，而三维交叉相关会处理视频医学图像气象地图等。我们经常使用的二维交叉相关通常用于处理图像。

4、总结

三、代码

1、互相关运算

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):  #@save
    """计算二维互相关运算"""
    #卷积矩阵的长宽
    h, w = K.shape
    #输出矩阵
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            #卷积核大小的X与卷积核相乘求和得到输出
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

2、卷积层

#跟上述的功能相同，只是创建的继承nn.Module的卷积类
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        #生成kernel大小的权重矩阵
        self.weight = nn.Parameter(torch.rand(kernel_size))
        #偏置全部设为1
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

3、卷积核

# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

for i in range(10):
    #使用卷积层对X进行前向传播，得到预测值Y_hat
    Y_hat = conv2d(X)
    #计算预测值和真实值之间的平方误差损失
    l = (Y_hat - Y) ** 2
    ## 将卷积层的梯度清零
    conv2d.zero_grad()
    #计算损失对卷积核的梯度
    l.sum().backward()
    # 迭代卷积核，使用梯度下降法
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')