一.算法快速幂

今天刷到两个题,比较有意思,还是记录一下.
先来讲讲50题.

LeetCode50(Pow(x,n))

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

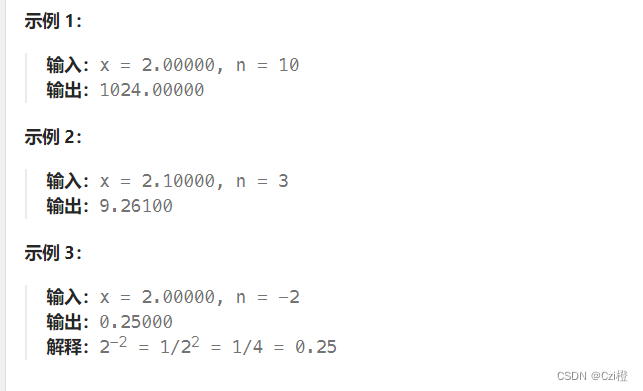
这道题一看很平常啊,不就一直乘嘛,循环走一次就够了.但是很抱歉,单纯的想法终究迎来了超时.而且还是个中等的题目,意识到没那么简单.我们需要换种思路.

对于2的128次方,如果我们需要一次次循环遍历,得需要128次才能计算得出.
而我们仔细把128拆分可以发现
2 * 2 = 2²
2² * 2² = 2⁴
2⁴ * 2⁴ = 2^8
2^8 * 2^8 = 2^16
2^16 * 2^16 = 2^32
2^32 * 2^32 = 2^64
2^64 * 2^64 = 2^128
我们只需要7次就能得到答案.
那有人就问了,你这是2的次数幂可以这样算而已.那我们对于不是2的整数幂如何处理呢?
例如7的105次方,我们可以将它进行拆分
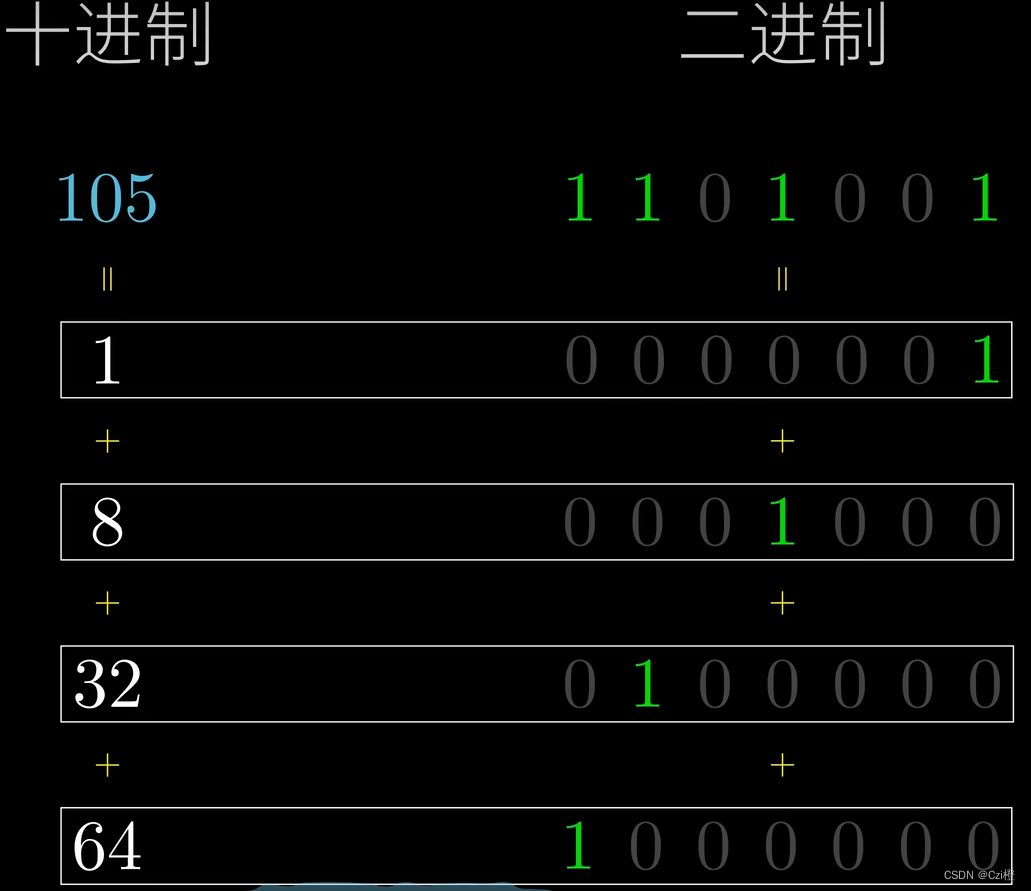
这样不好看105,我们转化成2进制试试.
0110 1001
即等于 7^64+ 7^32 + 7^8 + 7^1 = 7^105.

是不是我们每次都能拆分成2的整数幂
对于7*64我们可不可以通过之前的快速幂得到,答案是肯定的,

那我们怎么去判定什么时候需要去进行这个拆分的相乘呢?在上图中我们注意到,我们需要的快速幂的数都是正好二进制置为1的数.我们只需要去进行取余,只要末尾数为1时,此时我们需要将快速幂的结果相乘,其余步骤只做乘数的累加即可.每进行一次将次方数除二.
我们写出伪代码

function quickPow(a,n)
	r = 1
	while n != 0
		if n mod 2 == 1
			r = r * a
		a=a*a
		n = n/2
	return r

即可以通过这张图这样理解

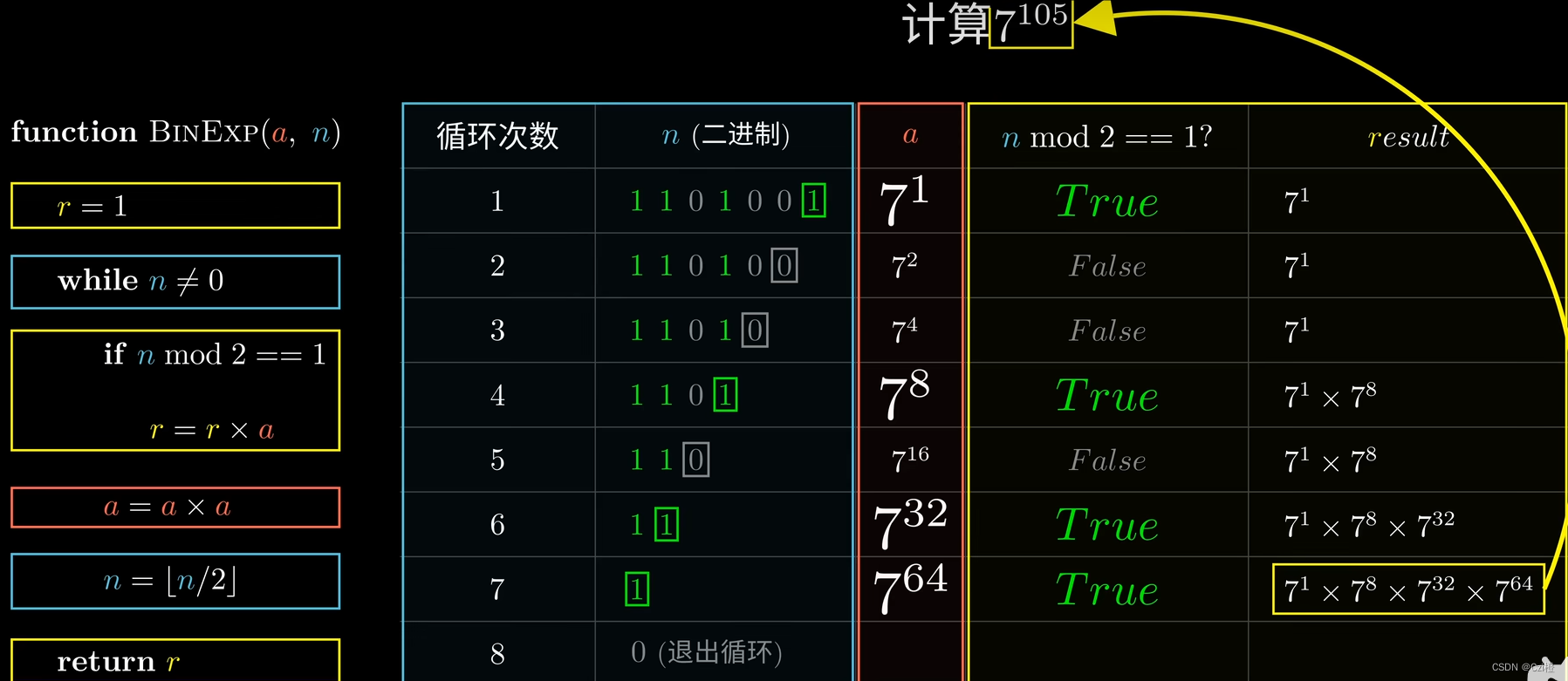
那我们还可以进一步优化这段代码.取余的运算我们可以对1做&运算.
而对于除以2我们可以右移一位来实现.

而对于这道题,我们还需要注意一点,就是有负数次幂的时候.其实本质上是一样的,因为负数次幂实际上就等于 1 / a^n.所以最终代码为

class Solution {
    public double myPow(double x, long n) {
        return n >= 0? quickPow(x,n): 1 / quickPow(x,-n);
    }
    public double quickPow(double x,long n){
        double r = 1.0;
        while(n != 0){
            if((n % 2) == 1){
                r = r * x; 
            }
            x = x * x;
            n = n >> 1;
        }
        return r;
    }
}

LeetCode70(爬楼梯)

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

这道题其实我们有几种解法,我介绍两种解法.
第一种,来复习一下动态规划.根据题目我们可以列式子
F(n) = F(n-1) + F(n-2);

即对于任意一个台阶都等于前一个台阶的次数加上前两个台阶的次数.
对于0阶台阶,我们只有一种方法到达,而对于1阶台阶我们也是只有一种方法到达.对于F(2),即2阶台阶,我们有两种方式到达,走两步或者一次性走两步.根据公式也能推导F(2) = F(1) + F(0).依次类推F(3) = F(2) + F(1) = 3次
F(4) = F(3) + F(2) = 5次…

所以每一阶都是前两阶之和.代码为

class Solution {
    public int climbStairs(int n) {
        int f1 = 0,f2 = 0,step = 1;
        for(int i = 0;i < n;i++){
            f1 = f2;
            f2 = step;
            step = f1 + f2;
        }
        return step;
    }
}

那我们如何利用之前提到过的快速幂解决这个问题呢.我们可以利用矩阵.

我们仔细来看看这个表达式

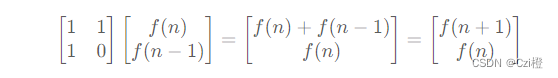
而对于[{f(n),f(n-1)}]的矩阵我们依旧可以像这样展开,所以最终能得到

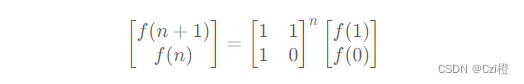
这不就是个幂等式吗,所以依照之前的模板.代码为

public class Solution {
    public int climbStairs(int n) {
        int[][] q = {{1, 1}, {1, 0}}; //定义之前分析到的结果的矩阵
        int[][] res = pow(q, n);
        return res[0][0];
    }

    public int[][] quickPow(int[][] q, int n) {
        int[][] result = {{1, 0}, {0, 1}}; //单元矩阵
        while (n > 0) {
            if ((n & 1) == 1) {
                result = mul(result , q);
            }
            q = mul(q, q);
            n >>= 1;
        }
        return result ;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                res [i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j];
            }
        }
        return res ;
    }
}

注意: 大家有没有发现一个点啊,这玩意的公式有点像那个.斐波那契是叭.
都是F(n) = F(n-1) + F(n-2)
那对于求斐波那契的多少项我们是不是同样能够这样处理.所以我们求斐波那契的代码和这个是一致的.