引言
聚类是一种强大的机器学习方法,用于根据特征空间中元素的接近程度发现相似的模式。它广泛用于计算机科学、生物科学、地球科学和经济学。尽管已经开发了最先进的基于分区和基于连接的聚类方法,但数据中的弱连接性和异构密度阻碍了其有效性。在这项工作中,我们提出了一种使用局部方向中心性(CDC)的边界搜索聚类算法。它采用基于 K 最近邻 (KNN) 分布的密度无关度量来区分内部点和边界点。边界点生成封闭的笼子来绑定内部点的连接,从而防止跨聚类连接并分离弱连接的聚类。我们通过在具有挑战性的合成数据集中检测复杂的结构簇,从单细胞RNA测序(scRNA-seq)和质谱细胞术(CyTOF)数据中识别细胞类型,识别语音语料库上的说话者,并在各种类型的真实世界基准上作证,来证明CDC的有效性。
TDCM(或ratio)是通过二维空间中三角不规则网络 (TIN) 的图论分析来估计的。通常,边界点往往比内部点具有较低的中心性(即较高的 DCM)。因此,我们按降序对所有 DCM 进行排序,如果给定边界点数,则可以搜索最佳 TDCM(或ratio)。
聚类算法的过程
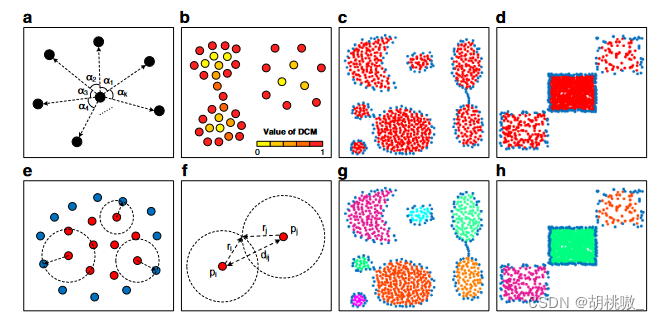
CDC的核心思想是根据KNN的分布来区分集群的边界点和内部点。边界点勾勒出簇的形状,并生成笼子以绑定内部点的连接。簇的内部点趋向于在各个方向上都被相邻点包围,而边界点仅包括一定方向范围内的相邻点。为了测量方向分布的这种差异,我们将 KNN 在 2D 空间中形成的角度方差定义为局部方向中心度量 (DCM):
D
C
M
=
1
k
∑
i
=
1
k
(
α
i
−
2
π
k
)
2
DCM =\frac{1}{k}\sum\limits_{i=1}^{k}(\alpha_i-\frac{2\pi}{k})^2
DCM=k1i=1∑k(αi−k2π)2
中心点的 KNNs 可以形成 k 个角 α1、α2…αk(图a)。对于二维角,条件
∑
i
=
1
k
α
i
=
2
π
\sum_{i=1}^{k}\alpha_i=2\pi
∑i=1kαi=2π成立。当且仅当所有角度相等时,DCM 达到最小值 0。这种情况意味着中心点的 KNN 在所有方向上均匀分布。当其中一个角度为 2π 而其余角度为 0 时,它可以最大化为
4
(
k
−
1
)
n
2
k
2
\frac{4(k-1)n^2}{k^2}
k24(k−1)n2。当 KNN 沿同一方向分布时,就会发生这种极端情况。根据极值,DCM 可以归一化为 [0, 1] 范围,如下所示:
D
C
M
=
k
4
(
k
−
1
)
n
2
∑
i
=
1
k
(
α
i
−
2
π
k
)
2
DCM =\frac{k}{4(k-1)n^2}\sum\limits_{i=1}^{k}(\alpha_i-\frac{2\pi}{k})^2
DCM=4(k−1)n2ki=1∑k(αi−k2π)2
DCM计算结果表明,团簇内部点的DCM值相对较低,边界点的DCM值较高(图b)。因此,内部点和边界点可以用阈值TDCM划分。DS5 和 DS7 两个合成数据集的划分结果验证了其有效性(图c、d)。为了保证内部点 p1, p2, …,pm 在周围边界点 q1, q2, …, qn−m 限制的区域内相互连接,我们将内部点 pi 与所有边界点之间的最小距离定义为其可到达距离:
r
i
=
m
i
n
j
=
1
n
−
m
d
(
p
i
,
q
j
)
r_i=min_{j=1}^{n-m}d(p_i,q_j)
ri=minj=1n−md(pi,qj)
其中 d(pi,qj) 是两点 pi 和 qj 之间的距离(图 e)。如果保证以下关联规则,则两个内部点可以连接为同一簇:
d
(
p
i
,
p
j
)
≤
r
i
+
r
j
d(p_i,p_j) \leq{r_i+r_j}
d(pi,pj)≤ri+rj
其中 ri 和 rj 分别是内部点 pi 和 pj 的可达距离(图f)。在正确识别边界点的前提下(边界点识别不完全的极端情况除外),内部点的连接被限制在边界点定义的区域内。如果两个内部点之间存在跨聚类连接,则边界点将包含在由其可到达距离定义的范围内,这与可到达距离的定义相冲突。因此,同一聚类的内部点可以被困在由边界点组成的同一外部轮廓中,并且基于此关联规则将避免跨聚类连接。DS5 和 DS7 的连接结果是通过将规则应用于除法结果而生成的(图 g、h)。虽然DS5和DS7中的簇对连接较弱,DS7中的三个簇的密度差异很大,但所有簇都被准确识别。
在计算 DCM 并连接内部点后,我们通过将每个边界点分配给其最近的内部点所属的集群来完成该过程。CDC 包含两个可控参数,k 和 TDCM。k 调整最近邻的数量,TDCM 确定内部点和边界点的划分。CDC的伪代码详见附注2。在实践中,考虑到 TDCM 随数据分布而变化,我们采用内部点的百分位数比率ratio来确定 TDCM 作为按降序排序的[n∙(1–ratio)]的 DCM。参数ratio具有直观的物理含义和更好的稳定性,这使得它比TDCM更容易指定。根据我们的实验,70%~99%的内点是建议的默认参数比率范围,以获得有希望的聚类结果。然而,当聚类相互混合时,需要更多的边界点(较低的比率)来分离闭合的聚类。
k的经验估计方法
通过对参数敏感度的分析和已有的研究,我们知道k是一个不敏感的参数,与数据集中的点数n有关。因此,我们提出了一种经验方法,将 k 和 n 之间的关系形式化为:
k
=
{
⌈
π
50
⌉
−
⌈
π
20
⌉
if
100
≤
n
≤
1000
⌈
l
o
g
2
(
n
)
+
10
⌉
−
5
⌈
l
o
g
2
(
n
)
⌉
if
n
≥
1000
k=\begin{cases} \lceil\frac{\pi}{50}\rceil- \lceil\frac{\pi}{20}\rceil&\text{if }100\leq n\le1000 \\ \lceil log_2(n)+10\rceil-5\lceil log_2(n)\rceil &\text{if } n\geq1000 \end{cases}
k={⌈50π⌉−⌈20π⌉⌈log2(n)+10⌉−5⌈log2(n)⌉if 100≤n≤1000if n≥1000
⌈
⌉
\lceil \quad \rceil
⌈⌉表示向上取整。
估计用于确定TDCM的边界点数:

构建了一个三角不规则网络(TIN)(图a)来连接所有点。在图论中,顶点的度数定义为入射到顶点的边数,每条边连接两个顶点。基于这一定律
∑
i
=
1
V
d
e
g
(
v
i
)
=
2
E
\sum_{i=1}^{V}deg(v_i)=2E
i=1∑Vdeg(vi)=2E
deg(vi) 表示顶点 vi 的度数,V 表示顶点总数,E 表示边的总数。
对于具有单个连接分量的 TIN,边界点的总数等于最外边的总数。
∑
i
=
1
V
d
e
g
(
v
i
)
=
3
F
+
B
\sum_{i=1}^{V}deg(v_i)=3F+B
i=1∑Vdeg(vi)=3F+B
F 和 B 分别表示三角形和边界点的总数。
二维欧拉公式:
V
+
F
−
E
=
1
V+F-E=1
V+F−E=1
通过结合这些公式,我们可以推断出 B 的解如下:
B
=
2
V
−
F
−
2
B=2V-F-2
B=2V−F−2
但是,整个 TIN 中的初始边界点数不等于分离聚类中的边界点总数。为了进行准确的估计,应将整个 TIN 视为多个子网(图 b)。给定 C 簇,簇中的边界点数可以求解如下:
∑
i
=
1
m
B
i
=
2
∑
i
=
1
m
V
i
−
∑
i
=
1
m
F
i
−
2
C
\sum_{i=1}^{m}B_i=2\sum_{i=1}^{m}V_i-\sum_{i=1}^{m}F_i-2C
i=1∑mBi=2i=1∑mVi−i=1∑mFi−2C
B
=
2
V
−
F
−
2
C
B=2V-F-2C
B=2V−F−2C
其中 F 是多个分离网络中簇内三角形的总数。V 在给定数据集(即 n)中是已知的,但 F 和 C 不是。初始F是整个TIN中三角形的总数,其中包括连接不同聚类的三角形,即三个顶点不都在同一聚类中的跨聚类三角形(否则为聚类内三角形)。使用过多的三角形会使边界点 B 的数量小于真实值。为了识别跨聚类三角形,我们设置了一个判断规则:
∑
i
=
1
3
∑
j
=
1
,
j
≠
i
3
σ
(
v
i
,
v
j
)
<
3
\sum_{i=1}^{3}\sum_{j=1,j\ne i}^{3}\sigma(v_i,v_j)<3
i=1∑3j=1,j=i∑3σ(vi,vj)<3
其中 v1、v2、v3 是三角形的三个顶点,σ(vi, vj)isan 指标函数:
σ
(
v
i
,
v
j
)
=
{
0
,
if
v
j
∉
KNN
(
v
i
)
1
,
if
v
j
∈
KNN
(
v
i
)
\sigma(v_i,v_j)=\begin{cases} 0, &\text{if }v_{j}\notin \text {KNN}(v_i) \\ 1, &\text{if }v_{j}\in \text {KNN}(v_i) \end{cases}
σ(vi,vj)={0,1,if vj∈/KNN(vi)if vj∈KNN(vi)
考虑聚类内三角形中顶点的邻近性。最终的F可以计算为初始F减去满足方程(16)的跨聚类三角形的数量(图c)。就簇C的数量而言,通常远小于V和F,这对B的估计有微不足道的影响,此外,CDC对DCM阈值的鲁棒性如讨论所述。因此,当 C 模糊或难以确定时,可以将其视为 1。
Code availability
The code of CDC in MATLAB, R and Python, and the toolkit with six applications can be downloaded at https://github.com/ZPGuiGroupWhu/ClusteringDirectionCentrality and https://zenodo.org/record/7029720#.YwuFsuxByZw. Digital Object Identifier https:// doi.org/10.5281/zenodo.7029720.
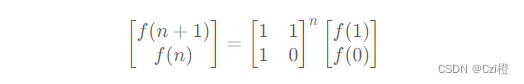








![[工业网络] 模型建立](https://img-blog.csdnimg.cn/img_convert/bdabc0f83323fdd4846e786e4418473d.jpeg)