基于遗传算法卡车无人机旅行推销员问题（Matlab代码实现）

news2025/11/1 2:40:54

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

📋1 概述

📝2 运行结果

📃3 参考文献

📋4 Matlab代码实现

📋1 概述

本文利用遗传算法解决了卡车无人机串联或包裹递送操作（即UPS，FedEx）的旅行推销员问题的“最后一英里”问题。每辆卡车都携带一架无人机，该无人机从一个站点发射，将范围内的包裹运送到附近的站点，同时与卡车并行运行。卡车和无人机并行工作以运送包裹。无人机受到航程和容量的限制。因此，它必须作为操作在卡车附近运行。操作是指卡车发射无人机，卡车和无人机运送到不同的位置，然后卡车在会合地点回收无人机以进行电池更换和装载。这个想法是确定卡车和无人机（以及操作）的路线，以最大限度地减少总时间。总时间基于操作（启动-交付-恢复）的时间。操作（卡车或无人机）的最大时间用于计算路径的总时间。

📝2 运行结果

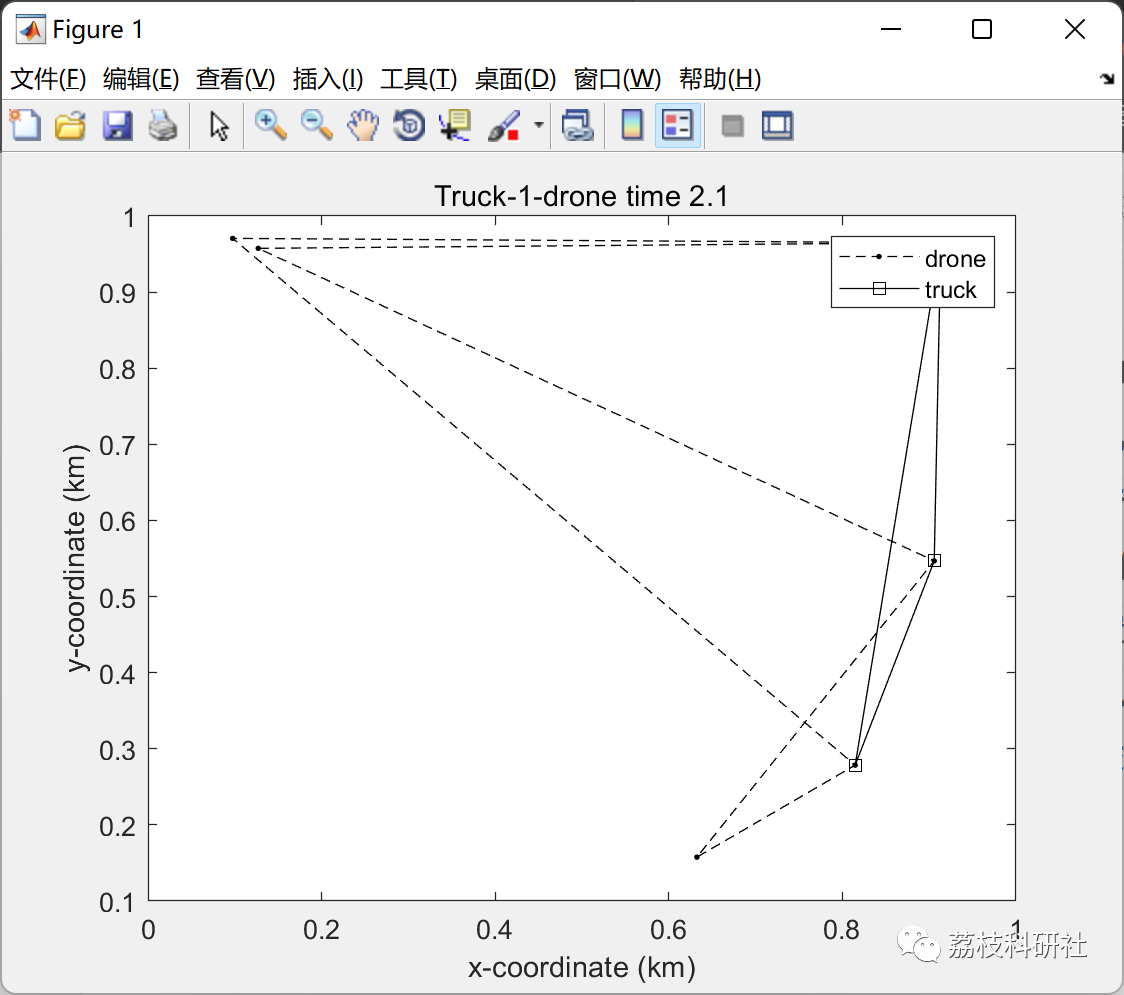
部分代码：

% Find the Best Route in the Population
[minDist,index] = min(totalDist);
distHistory(iter) = minDist;
if minDist < globalMin
globalMin = minDist;
optPop2 = pop2(index,:);
optPop1 = pop(index,:);
if showprogress % gaph results

tr_route = (optPop2==0).*optPop1;
tr_route = tr_route(tr_route>0);
tr_route = [tr_route tr_route(1)];
if optPop2(n)==1
dr_route = [optPop1 optPop1(1) ];
else
dr_route = [optPop1 ];
end
plot(xy(dr_route,1), xy(dr_route,2), 'k.--'); hold on;
plot(xy(tr_route,1), xy(tr_route,2),'ks-');
xlabel('x-coordinate (km)');
ylabel('y-coordinate (km)');
legend('drone','truck');
title(sprintf('Truck-1-drone time %1.1f',minDist));
hold off;
drawnow;
end
end

% Genetic Algorithm Operators
randomOrder = randperm(popSize);

for p = 5:5:popSize
% basically a random sampling in matrix format with a
rtes = pop(randomOrder(p-4:p),:);

dists = totalDist(randomOrder(p-4:p));
% what are the min distances?
[~,idx] = min(dists);
% what is the best route
bestOf5Route = rtes(idx,:);

% randomly select two route insertion points and sort
routeInsertionPoints = sort(ceil(n*rand(1,2)));

I = routeInsertionPoints(1);
J = routeInsertionPoints(2);

for k = 1:5 % Mutate the Best row (dist) to get Three New Routes and orig.
% a small matrix of 4 rows of best time
tmpPop(k,:) = bestOf5Route;

switch k
% flip two of the cities and cities between
case 2 % Flip
tmpPop(k,I:J) = tmpPop(k,J:-1:I);

case 3 % Swap
tmpPop(k,[I J]) = tmpPop(k,[J I]);
case 4 % Slide segment
tmpPop(k,I:J) = tmpPop(k,[I+1:J I]);
% tmpPop2(k,I2)=flag;
case 5 % increment sequence one space
tmpPop(k,1:end) = tmpPop(k,[2:end 1]);

otherwise % Do Nothing
end
end
% using the original population, create a new population
newPop(p-4:p,:) = tmpPop;
end
pop = newPop; % update entire populations with mutations

end
res=[optPop2;
optPop1]
end