Python_机器学习_算法_第7章_7.拓展知识

7.拓展知识

7.1. 其他距离公式

1 标准化欧氏距离

标准化欧氏距离(Standardized EuclideanDistance)是针对欧氏距离的缺点而作的一种改进。

思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。

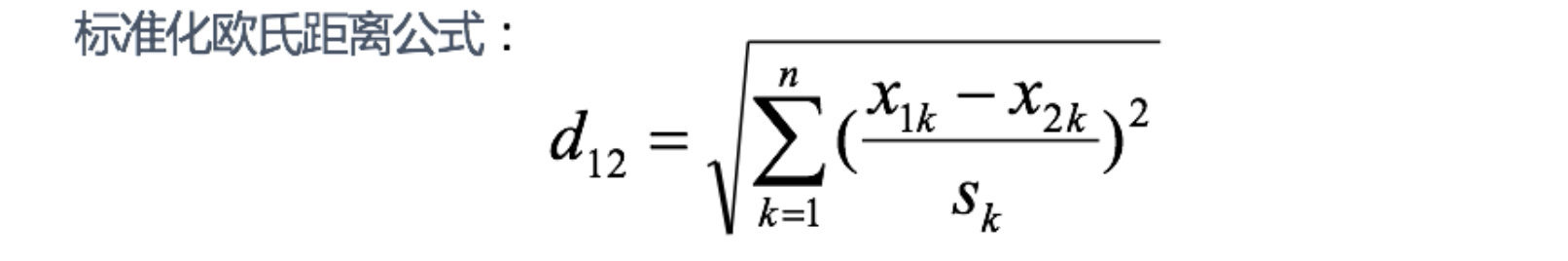
tips: Sk表示各个维度的标准差

如果将方差的倒数看成一个权重，也可称之为加权欧氏距离(Weighted Euclidean distance)。

举例:

X=[[1,1],[2,2],[3,3],[4,4]];（假设两个分量的标准差分别为0.5和1）
经计算得:
d =   2.2361    4.4721    6.7082    2.2361    4.4721    2.2361

2 余弦距离

几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异，就是余弦距离(Cosine Distance)。

• 二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

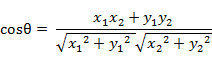
• 两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为：

即：

夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1，当两个向量的方向完全相反余弦取最小值-1。

举例:

X=[[1,1],[1,2],[2,5],[1,-4]]
经计算得:
d =   0.9487    0.9191   -0.5145    0.9965   -0.7593   -0.8107

3 汉明距离【了解】

两个等长字符串s1与s2的汉明距离(Hamming Distance)为：将其中一个变为另外一个所需要作的最小字符替换次数。

例如:

  The Hamming distance between "1011101" and "1001001" is 2. 
  The Hamming distance between "2143896" and "2233796" is 3. 
  The Hamming distance between "toned" and "roses" is 3.

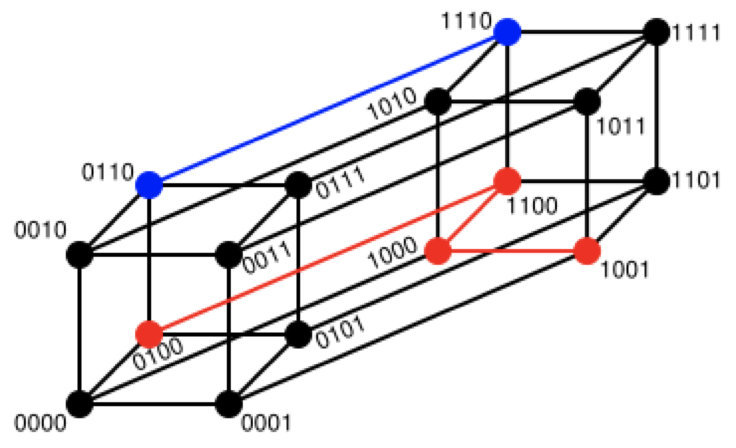
随堂练习：
求下列字符串的汉明距离：

  1011101与 1001001 　

  2143896与 2233796 
　
  irie与 rise

汉明重量：是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是 1 的个数，所以 11101 的汉明重量是 4。因此，如果向量空间中的元素a和b之间的汉明距离等于它们汉明重量的差a-b。

应用：汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中，为了增强容错性，应使得编码间的最小汉明距离尽可能大。但是，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。

举例:

X=[[0,1,1],[1,1,2],[1,5,2]]
注：以下计算方式中，把2个向量之间的汉明距离定义为2个向量不同的分量所占的百分比。

经计算得:
d =   0.6667    1.0000    0.3333

4 杰卡德距离【了解】

杰卡德相似系数(Jaccard similarity coefficient)：两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示：

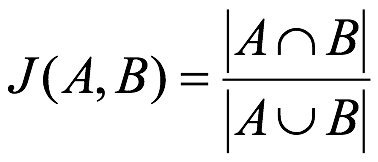
杰卡德距离(Jaccard Distance)：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：

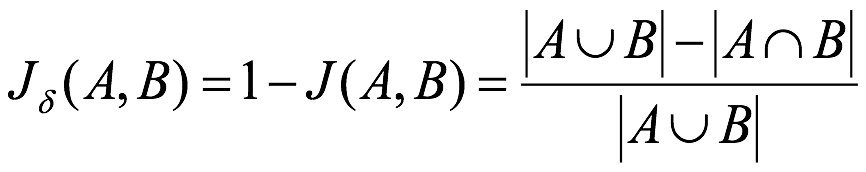
举例:

X=[[1,1,0],[1,-1,0],[-1,1,0]]
注：以下计算中，把杰卡德距离定义为不同的维度的个数占“非全零维度”的比例
经计算得:
d =   0.5000    0.5000    1.0000

5 马氏距离【了解】

下图有两个正态分布图，它们的均值分别为a和b，但方差不一样，则图中的A点离哪个总体更近？或者说A有更大的概率属于谁？显然，A离左边的更近，A属于左边总体的概率更大，尽管A与a的欧式距离远一些。这就是马氏距离的直观解释。

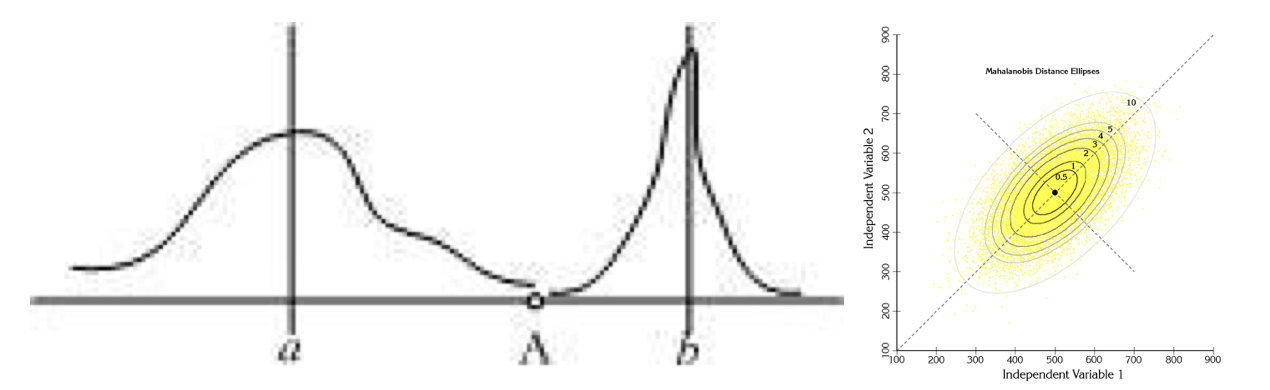
马氏距离(Mahalanobis Distance)是基于样本分布的一种距离。

马氏距离是由印度统计学家马哈拉诺比斯提出的，表示数据的协方差距离。它是一种有效的计算两个位置样本集的相似度的方法。

与欧式距离不同的是，它考虑到各种特性之间的联系，即独立于测量尺度。

**马氏距离定义：**设总体G为m维总体（考察m个指标），均值向量为μ=（μ1，μ2，… …，μm，）`,协方差阵为∑=（σij）,

则样本X=（X1，X2，… …，Xm，）`与总体G的马氏距离定义为：

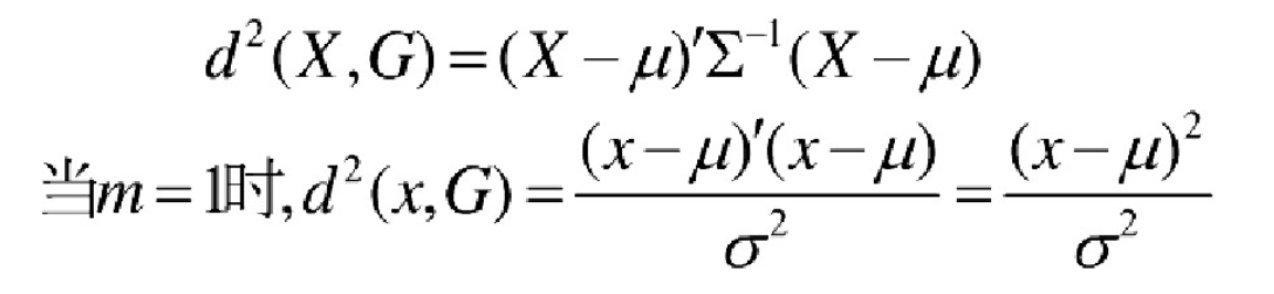
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为∑的随机变量的差异程度：如果协方差矩阵为单位矩阵，马氏距离就简化为欧式距离；如果协方差矩阵为对角矩阵，则其也可称为正规化的欧式距离。

马氏距离特性：

1.量纲无关，排除变量之间的相关性的干扰；

2.马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；

3 .计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。

4.还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如三个样本点（3，4），（5，6），（7，8），这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧式距离计算。

欧式距离&马氏距离：

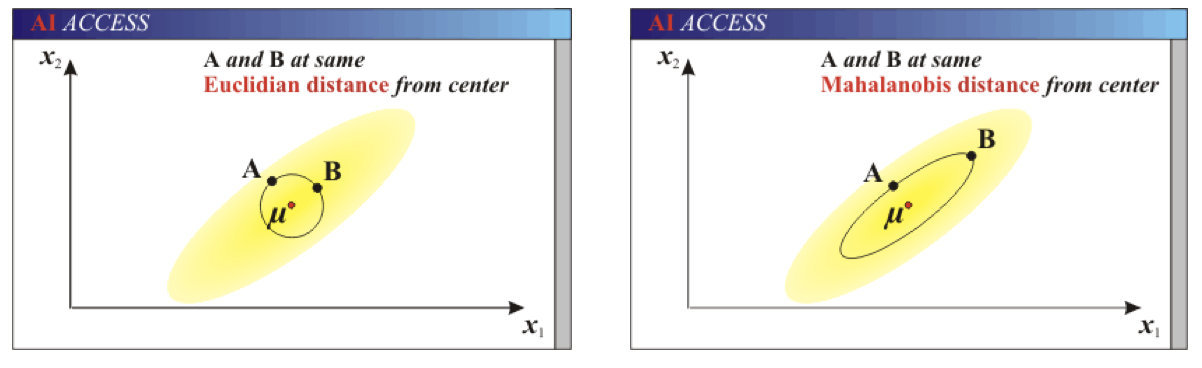
举例：

已知有两个类G1和G2，比如G1是设备A生产的产品，G2是设备B生产的同类产品。设备A的产品质量高（如考察指标为耐磨度X），其平均耐磨度μ1=80，反映设备精度的方差σ2(1)=0.25;设备B的产品质量稍差，其平均耐磨损度μ2=75，反映设备精度的方差σ2(2)=4.

今有一产品G0，测的耐磨损度X0=78，试判断该产品是哪一台设备生产的？

直观地看，X0与μ1（设备A）的绝对距离近些，按距离最近的原则，是否应把该产品判断设备A生产的？

考虑一种相对于分散性的距离，记X0与G1，G2的相对距离为d1，d2,则：

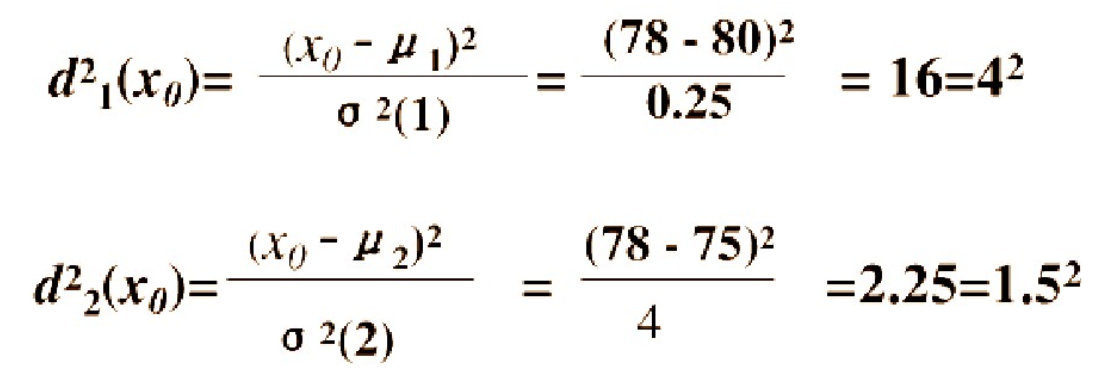
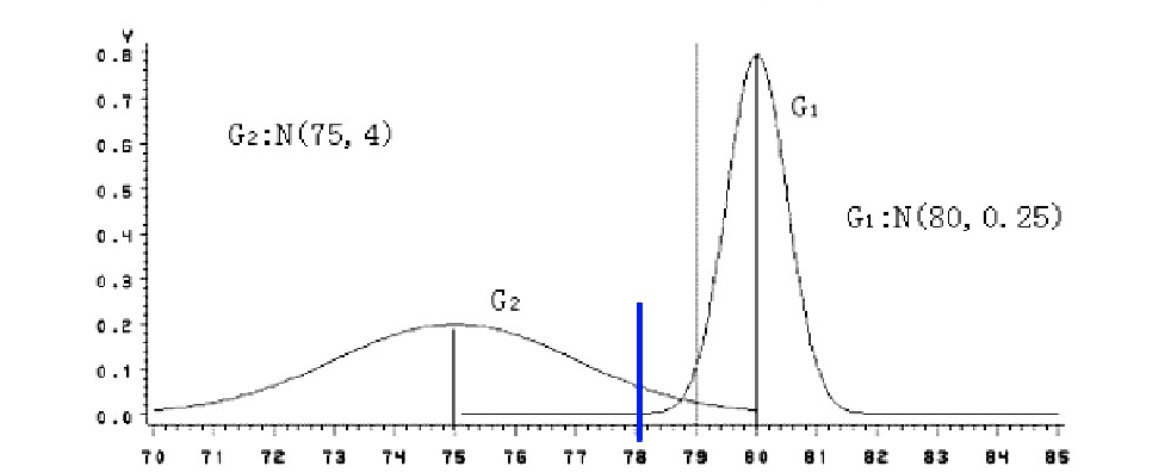
因为d2=1.5 < d1=4，按这种距离准则，应判断X0为设备B生产的。

设备B生产的产品质量较分散，出现X0为78的可能性较大；而设备A生产的产品质量较集中，出现X0为78的可能性较小。

这种相对于分散性的距离判断就是马氏距离。

7.2.再议数据分割

前面已经讲过，我们可通过实验测试来对学习器的泛化误差进行评估并进而做出选择。

为此，需使用一个“测试集”( testing set)来测试学习器对新样本的判别能力，然后以测试集上的“测试误差” (testing error)作为泛化误差的近似。

通常我们假设测试样本也是从样本真实分布中独立同分布采样而得。但需注意的是，测试集应该尽可能与训练集互斥。

互斥，即测试样本尽量不在训练集中出现、未在训练过程中使用过。

测试样本为什么要尽可能不出现在训练集中呢？为理解这一点，不妨考虑这样一个场景:

老师出了10道习题供同学们练习，考试时老师又用同样的这10道题作为试题，这个考试成绩能否有效反映出同学们学得好不好呢？

答案是否定的，可能有的同学只会做这10道题却能得高分。

回到我们的问题上来，我们希望得到泛化性能强的模型，好比是希望同学们对课程学得很好、获得了对所学知识“举一反三”的能力；训练样本相当于给同学们练习的习题，测试过程则相当于考试。显然，若测试样本被用作训练了，则得到的将是过于“乐观”的估计结果。

可是，我们只有一个包含m个样例的数据集

既要训练，又要测试，怎样才能做到呢？

• 答案是:通过对D进行适当的处理，从中产生出训练集S和测试集T。（这个也是我们前面一直在做的事情）。

下面我们一起总结一下几种常见的做法：

• 留出法
• 交叉验证法
• 自助法

---

1 留出法

“留出法”(hold-out)直接将数据集D划分为两个互斥的集合，其中一个集合作为训练集S，另一个作为测试集T，即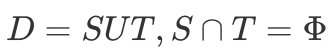。在S上训练出模型后，用T来评估其测试误差，作为对泛化误差的估计。

大家在使用的过程中，需注意的是，训练/测试集的划分要尽可能保持数据分布的一致性，避免因数据划分过程引入额外的偏差而对最终结果产生影响，例如在分类任务中至少要保持样本的类别比例相似。

如果从采样( sampling)的角度来看待数据集的划分过程，则保留类别比例的采样方式通常称为**“分层采样”( stratified sampling)。**

例如通过对D进行分层样而获得含70%样本的训练集S和含30%样本的测试集T，

若D包含500个正例、500个反例，则分层采样得到的S应包含350个正例、350个反例，而T则包含150个正例和150个反例；

若S、T中样本类别比例差别很大，则误差估计将由于训练/测试数据分布的差异而产生偏差。

另一个需注意的问题是，即便在给定训练测试集的样本比例后，仍存在多种划分方式对初始数据集D进行分割。

例如在上面的例子中，可以把D中的样本排序，然后把前350个正例放到训练集中，也可以把最后350个正例放到训练集中，这些不同的划分将导致不同的训练/测试集，相应的，模型评估的结果也会有差别。

因此，单次使用留出法得到的估计结果往往不够稳定可靠，在使用留出法时，一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。

例如进行100次随机划分，每次产生一个训练/测试集用于实验评估，100次后就得到100个结果，而留出法返回的则是这100个结果的平均。

此外，我们希望评估的是用D训练出的模型的性能，但留出法需划分训练/测试集，这就会导致一个窘境:

• 若令训练集S包含绝大多数样本，则训练出的模型可能更接近于用D训练出的模型，但由于T比较小，评估结果可能不够稳定准确；
• 若令测试集T多包含一些样本，则训练集S与D差别更大了，被评估的模型与用D训练出的模型相比可能有较大差别，从而降低了评估结果的保真性( fidelity)。

这个问题没有完美的解决方案，常见做法是将大约2/3~4/5的样本用于训练，剩余样本用于测试。

使用Python实现留出法：

from sklearn.model_selection import train_test_split
#使用train_test_split划分训练集和测试集
train_X , test_X, train_Y ,test_Y = train_test_split(
        X, Y, test_size=0.2,random_state=0)

在留出法中，有一个特例，叫：留一法( Leave-One-Out，简称LOO），即每次抽取一个样本做为测试集。

显然，留一法不受随机样本划分方式的影响，因为m个样本只有唯一的方式划分为m个子集一每个子集包含个样本；

使用Python实现留一法：

from sklearn.model_selection import LeaveOneOut

data = [1, 2, 3, 4]
loo = LeaveOneOut()
for train, test in loo.split(data):
    print("%s %s" % (train, test))
'''结果
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]
'''

留一法优缺点：

优点：

• 留一法使用的训练集与初始数据集相比只少了一个样本，这就使得在绝大多数情况下，留一法中被实际评估的模型与期望评估的用D训练出的模型很相似。因此，留一法的评估结果往往被认为比较准确。

缺点：

• 留一法也有其缺陷:在数据集比较大时，训练m个模型的计算开销可能是难以忍受的(例如数据集包含1百万个样本，则需训练1百万个模型，而这还是在未考虑算法调参的情况下。

2 交叉验证法

2.1 交叉验证法基本介绍

“交叉验证法”( cross validation)先将数据集D划分为k个大小相似的互斥子集，即。每个子集Di都尽可能保持数据分布的一致性，即从D中通过分层抽样得到。

然后，每次用k-1个子集的并集作为训练集，余下的那个子集作为验证集；这样就可获得k组训练/验证集，从而可进行k次训练和测试，最终返回的是这k个测试结果的均值。

显然，交叉验证法评估结果的稳定性和保真性在很大程度上取决于k的取值，为强调这一点，通常把交叉验证法称为“k折交叉验证”(k- fold cross validation)。k最常用的取值是10，此时称为10折交叉验证；其他常用的k值有5、20等。下图给出了10折交叉验证的示意图。

**与留出法相似，将数据集D划分为k个子集同样存在多种划分方式。**为减小因样本划分不同而引入的差别，k折交叉验证通常要随机使用不同的划分重复p次，最终的评估结果是这p次k折交叉验证结果的均值，例如常见的有 “10次10折交叉验证”。

交叉验证实现方法，除了咱们前面讲的GridSearchCV之外，还有KFold, StratifiedKFold

2.2 KFold和StratifiedKFold

from sklearn.model_selection import KFold,StratifiedKFold

• 用法：
  • 将训练/测试数据集划分n_splits个互斥子集，每次用其中一个子集当作验证集，剩下的n_splits-1个作为训练集，进行n_splits次训练和测试，得到n_splits个结果
  • StratifiedKFold的用法和KFold的区别是：SKFold是分层采样，确保训练集，测试集中，各类别样本的比例是和原始数据集中的一致。
• 注意点：
  • 对于不能均等分数据集，其前n_samples % n_splits子集拥有n_samples // n_splits + 1个样本，其余子集都只有n_samples // n_splits样本
• 参数说明：
  • n_splits：表示划分几等份
  • shuffle：在每次划分时，是否进行洗牌
    • ①若为Falses时，其效果等同于random_state等于整数，每次划分的结果相同
    • ②若为True时，每次划分的结果都不一样，表示经过洗牌，随机取样的
• 属性：
  • ①split(X, y=None, groups=None)：将数据集划分成训练集和测试集，返回索引生成器

import numpy as np
from sklearn.model_selection import KFold,StratifiedKFold

X = np.array([
    [1,2,3,4],
    [11,12,13,14],
    [21,22,23,24],
    [31,32,33,34],
    [41,42,43,44],
    [51,52,53,54],
    [61,62,63,64],
    [71,72,73,74]
])

y = np.array([1,1,0,0,1,1,0,0])

folder = KFold(n_splits = 4, random_state=0, shuffle = False)
sfolder = StratifiedKFold(n_splits = 4, random_state = 0, shuffle = False)

for train, test in folder.split(X, y):
    print('train:%s | test:%s' %(train, test))
    print("")

for train, test in sfolder.split(X, y):
    print('train:%s | test:%s'%(train, test))
    print("")

结果：

# 第一个for，输出结果为：
train:[2 3 4 5 6 7] | test:[0 1]

train:[0 1 4 5 6 7] | test:[2 3]

train:[0 1 2 3 6 7] | test:[4 5]

train:[0 1 2 3 4 5] | test:[6 7]

# 第二个for，输出结果为：
train:[1 3 4 5 6 7] | test:[0 2]

train:[0 2 4 5 6 7] | test:[1 3]

train:[0 1 2 3 5 7] | test:[4 6]

train:[0 1 2 3 4 6] | test:[5 7]

可以看出，sfold进行4折计算时候，是平衡了测试集中，样本正负的分布的；但是fold却没有。

3 自助法

我们希望评估的是用D训练出的模型。但在留出法和交叉验证法中，由于保留了一部分样本用于测试，因此**实际评估的模型所使用的训练集比D小，**这必然会引入一些因训练样本规模不同而导致的估计偏差。留一法受训练样本规模变化的影响较小，但计算复杂度又太高了。

有没有什么办法可以减少训练样本规模不同造成的影响，同时还能比较高效地进行实验估计呢？

“自助法”( bootstrapping)是一个比较好的解决方案，它直接以自助采样法( bootstrap sampling)为基础。给定包含m个样本的数据集D，我们对它进行采样产生数据集D:

• 每次随机从D中挑选一个样本，将其拷贝放入D，然后再将该样本放回初始数据集D中，使得该样本在下次采样时仍有可能被到；
• 这个过程重复执行m次后，我们就得到了包含m个样本的数据集D′，这就是自助采样的结果。

显然，D中有一部分样本会在D′中多次出现，而另一部分样本不出现。可以做一个简单的估计，样本在m次采样中始终不被采到的概率是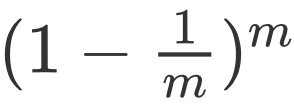，取极限得到

即通过自助采样，初始数据集D中约有36.8%的样本未出现在采样数据集D′中。

于是我们可将D′用作训练集，D\D′用作测试集；这样，实际评估的模型与期望评估的模型都使用m个训练样本，而我们仍有数据总量约1/3的、没在训练集中出现的样本用于测试。

这样的测试结果，亦称**“包外估计”(out- of-bagestimate）**

自助法优缺点：

• 优点：
  • 自助法在数据集较小、难以有效划分训练/测试集时很有用；
  • 此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处。
• 缺点：
  • 自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差。因此，在初始数据量足够时；留出法和交叉验证法更常用一些。

4 总结

综上所述：

• 当我们数据量足够时，选择留出法简单省时，在牺牲很小的准确度的情况下，换取计算的简便；
• 当我们的数据量较小时，我们应该选择交叉验证法，因为此时划分样本集将会使训练数据过少；
• 当我们的数据量特别少的时候，我们可以考虑留一法。

7.3. 正规方程的另一种推导方式

---

1.损失表示方式

总损失定义为：

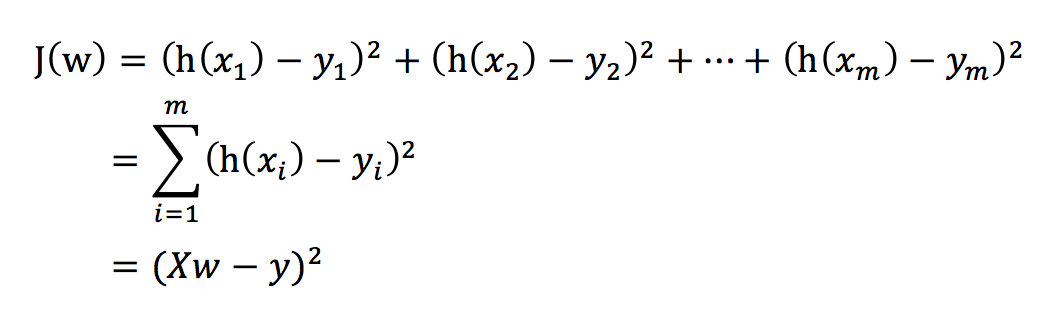
• yi为第i个训练样本的真实值
• h(xi)为第i个训练样本特征值组合预测函数
• 又称最小二乘法

2.另一种推导方式

把损失函数分开书写：

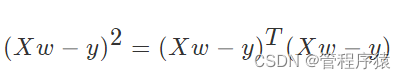
对展开上式进行求导：

需要求得求导函数的极小值，即上式求导结果为0，经过化解，得结果为：

经过化解为：

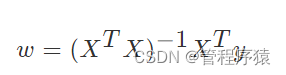
补充：需要用到的矩阵求导公式：

7.4.梯度下降法算法比较和进一步优化

常见的梯度下降算法有：

• 全梯度下降算法(Full gradient descent）,
• 随机梯度下降算法（Stochastic gradient descent）,
• 小批量梯度下降算法（Mini-batch gradient descent）,
• 随机平均梯度下降算法（Stochastic average gradient descent）

它们都是为了正确地调节权重向量，通过为每个权重计算一个梯度，从而更新权值，使目标函数尽可能最小化。其差别在于样本的使用方式不同。

我们通过一个数据集案例进行对比，查看他们的区别

1 算法比较

为了比对四种基本梯度下降算法的性能，我们通过一个逻辑二分类实验来说明。本文所用的Adult数据集来自UCI公共数据库（http://archive.ics.uci.edu/ml/datasets/Adult）。 数据集共有15081条记录，包括“性别”“年龄”“受教育情况”“每周工作时常”等14个特征，数据标记列显示“年薪是否大于50000美元”。我们将数据集的80%作为训练集，剩下的20%作为测试集，使用逻辑回归建立预测模型，根据数据点的14个特征预测其数据标记（收入情况）。

以下6幅图反映了模型优化过程中四种梯度算法的性能差异。

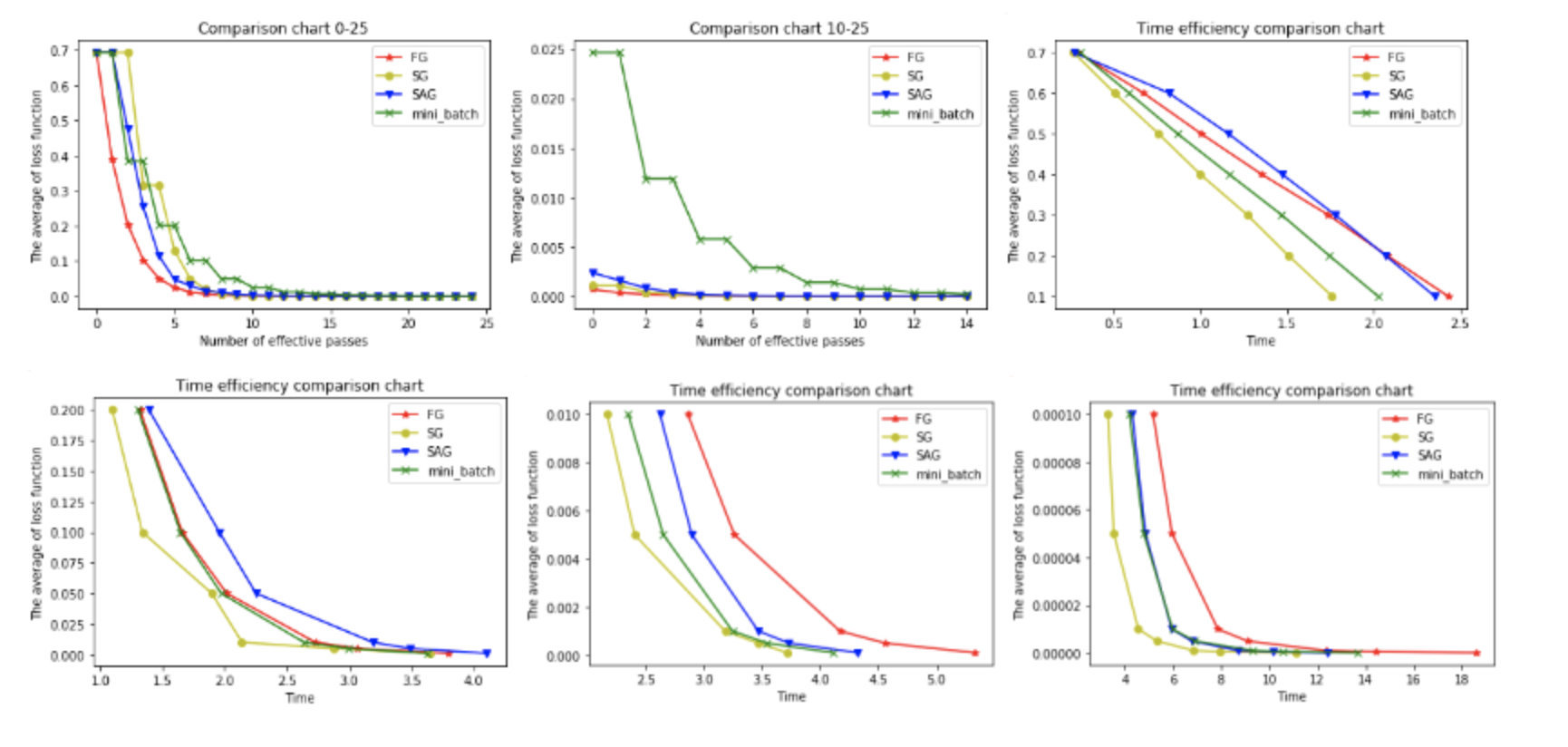
在图1和图2中，横坐标代表有效迭代次数，纵坐标代表平均损失函数值。图1反映了前25次有效迭代过程中平均损失函数值的变化情况，为了便于观察，图2放大了第10次到25次的迭代情况。

从图1中可以看到，四种梯度算法下，平均损失函数值随迭代次数的增加而减少。FG的迭代效率始终领先，能在较少的迭代次数下取得较低的平均损失函数值。FG与SAG的图像较平滑，这是因为这两种算法在进行梯度更新时都结合了之前的梯度；SG与mini-batch的图像曲折明显，这是因为这两种算法在每轮更新梯度时都随机抽取一个或若干样本进行计算，并没有考虑到之前的梯度。

从图2中可以看到**虽然四条折现的纵坐标虽然都趋近于0，但SG和FG较早，mini-batch最晚。**这说明如果想使用mini-batch获得最优参数，必须对其进行较其他三种梯度算法更多频次的迭代。

在图3，4，5，6中，横坐标表示时间，纵坐标表示平均损失函数值。

从图3中可以看出使用四种算法将平均损失函数值从0.7降到0.1最多只需要2.5s，由于本文程序在初始化梯度时将梯度设为了零，故前期的优化效果格外明显。其中SG在前期的表现最好，仅1.75s便将损失函值降到了0.1，虽然SG无法像FG那样达到线性收敛，但在处理大规模机器学习问题时，为了节约时间成本和存储成本，可在训练的一开始先使用SG，后期考虑到收敛性和精度可改用其他算法。

从图4，5，6可以看出，随着平均损失函数值的不断减小，SG的性能逐渐反超FG，FG的优化效率最慢，即达到相同平均损失函数值时FG所需要的时间最久。

综合分析六幅图我们得出以下结论：

（1**）FG方法由于它每轮更新都要使用全体数据集，故花费的时间成本最多，内存存储最大。**

（2）SAG在训练初期表现不佳，优化速度较慢。这是因为我们常将初始梯度设为0，而SAG每轮梯度更新都结合了上一轮梯度值。

（3）综合考虑迭代次数和运行时间，SG表现性能都很好，能在训练初期快速摆脱初始梯度值，快速将平均损失函数降到很低。但要注意，在使用SG方法时要慎重选择步长，否则容易错过最优解。

（4）mini-batch结合了SG的“胆大”和FG的“心细”，从6幅图像来看，它的表现也正好居于SG和FG二者之间。在目前的机器学习领域，mini-batch是使用最多的梯度下降算法，正是因为它避开了FG运算效率低成本大和SG收敛效果不稳定的缺点。

2 梯度下降优化算法

以下这些算法主要用于深度学习优化

• 动量法
  • 其实动量法(SGD with monentum)就是SAG的姐妹版
  • SAG是对过去K次的梯度求平均值
  • SGD with monentum 是对过去所有的梯度求加权平均
• Nesterov加速梯度下降法
  • 类似于一个智能球，在重新遇到斜率上升时候，能够知道减速
• Adagrad
  • 让学习率使用参数
  • 对于出现次数较少的特征，我们对其采用更大的学习率，对于出现次数较多的特征，我们对其采用较小的学习率。
• Adadelta
  • Adadelta是Adagrad的一种扩展算法，以处理Adagrad学习速率单调递减的问题。
• RMSProp
  • 其结合了梯度平方的指数移动平均数来调节学习率的变化。
  • 能够在不稳定（Non-Stationary）的目标函数情况下进行很好地收敛。
• Adam
  • 结合AdaGrad和RMSProp两种优化算法的优点。
  • 是一种自适应的学习率算法

参考链接：[https://blog.csdn.net/google19890102/article/details/69942970]

7.5 .第二章知识补充： 多项式回归

我们在前面讲的都是一般线性回归，即使用的假设函数是一元一次方程，也就是二维平面上的一条直线。

但是很多时候可能会遇到直线方程无法很好的拟合数据的情况，这个时候可以尝试使用多项式回归。

多项式回归中，加入了特征的更高次方（例如平方项或立方项），也相当于增加了模型的自由度，用来捕获数据中非线性的变化。添加高阶项的时候，也增加了模型的复杂度。随着模型复杂度的升高，模型的容量以及拟合数据的能力增加，可以进一步降低训练误差，但导致过拟合的风险也随之增加（后面会专门讨论出现过拟合的情况）。

1 多项式回归的一般形式

在多项式回归中，最重要的参数是最高次方的次数。设最高次方的次数为n，且只有一个特征时，其多项式回归的方程为：

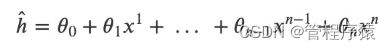
如果令x_0=1x0=1，在多样本的情况下，可以写成向量化的形式：

其中𝑋是大小为m⋅(n+1)的矩阵，θ是大小为(n+1)⋅1的矩阵。

在这里虽然只有一个特征x以及x的不同次方，但是也可以将x的高次方当做一个新特征。与多元回归分析唯一不同的是，这些特征之间是高度相关的，而不是通常要求的那样是相互对立的。

在这里有个问题在刚开始学习线性回归的时候困扰了自己很久：如果假设中出现了高阶项，那么这个模型还是线性模型吗？此时看待问题的角度不同，得到的结果也不同。如果把上面的假设看成是特征xx的方程，那么该方程就是非线性方程；如果看成是参数𝜃θ的方程，那么xx的高阶项都可以看做是对应𝜃θ的参数，那么该方程就是线性方程。很明显，在线性回归中采用了后一种解释方式。因此多项式回归仍然是参数的线性模型。

2 多项式回归的实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

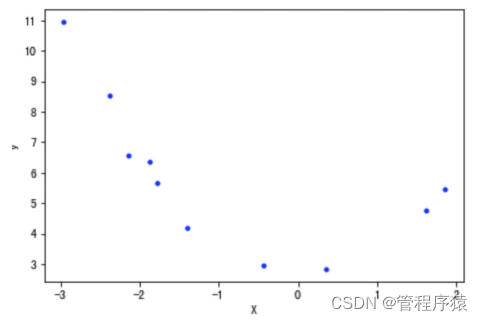
下是使用的数据是使用 y=x2+2 并加入一些随机误差生成的，只取了10个数据点：

# 构造数据,数据可视化展示
data = np.array([[ -2.95507616,  10.94533252],
                 [ -0.44226119,   2.96705822],
                 [ -2.13294087,   6.57336839],
                 [  1.84990823,   5.44244467],
                 [  0.35139795,   2.83533936],
                 [ -1.77443098,   5.6800407 ],
                 [ -1.8657203 ,   6.34470814],
                 [  1.61526823,   4.77833358],
                 [ -2.38043687,   8.51887713],
                 [ -1.40513866,   4.18262786]])

X = data[:, 0].reshape(-1, 1)  # 将array转换成矩阵
y = data[:, 1].reshape(-1, 1)

plt.plot(X, y, "b.")
plt.xlabel('X')
plt.ylabel('y')
plt.show()

2.1 直线方程的拟合

下面先用直线方程拟合上面的数据点

lin_reg = LinearRegression()
lin_reg.fit(X, y)
print(lin_reg.intercept_, lin_reg.coef_)  # [ 4.97857827] [[-0.92810463]]

X_plot = np.linspace(-3, 3, 1000).reshape(-1, 1)

# 可以使用两种方法用于模型预测
# y_plot = np.dot(X_plot, lin_reg.coef_.T) + lin_reg.intercept_
y_plot = lin_reg.predict(X_plot)

plt.plot(X_plot, y_plot,"red")
plt.plot(X, y, 'b.')
plt.xlabel('X')
plt.ylabel('y')

# 使用mse衡量其误差值:
y_pre = lin_reg.predict(X)
mean_squared_error(y, y_pre)
# 3.3363076332788495

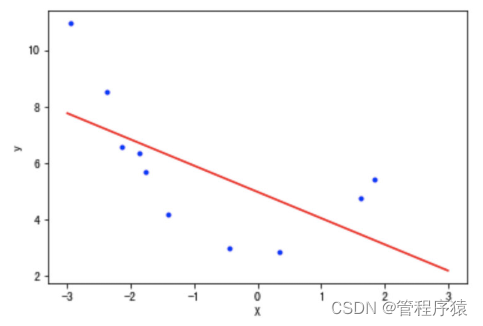
2.2 使用多项式方程

为了拟合2次方程，需要有特征x2的数据，这里可以使用函数"PolynomialFeatures"来获得：

sklearn 的 PolynomialFeatures 的用法

官方文档链接

使用 sklearn.preprocessing.PolynomialFeatures 这个类可以进行特征的构造，构造的方式就是特征与特征相乘（自己与自己，自己与其他人），这种方式叫做使用多项式的方式。 例如：有 𝑎、𝑏 两个特征，那么它的 2 次多项式的次数为 1,a,b,a2,ab,b2。

PolynomialFeatures 这个类有 3 个参数：

• degree：控制多项式的次数；
• interaction_only：默认为 False，如果指定为 True，那么就不会有特征自己和自己结合的项，组合的特征中没有 a2 和 b2 ；
• include_bias：默认为 True 。如果为 True 的话，那么结果中就会有 0 次幂项，即全为 1 这一列。

X = np.arange(6).reshape(3, 2)
X

# 输出结果
array([[0, 1],
       [2, 3],
       [4, 5]])

from sklearn.preprocessing import PolynomialFeatures
# 设置多项式阶数为2,其他值默认
# degree 多项式阶数
poly = PolynomialFeatures(degree=2)
res = poly.fit_transform(X)
res

# 输出结果
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

使用函数"PolynomialFeatures"获取二次方项：

poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
print(X_poly)

# 输出结果
[[-2.95507616  8.73247511]
 [-0.44226119  0.19559496]
 [-2.13294087  4.54943675]
 [ 1.84990823  3.42216046]
 [ 0.35139795  0.12348052]
 [-1.77443098  3.1486053 ]
 [-1.8657203   3.48091224]
 [ 1.61526823  2.60909145]
 [-2.38043687  5.66647969]
 [-1.40513866  1.97441465]]

利用上面的数据做线性回归分析：

lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
print(lin_reg.intercept_, lin_reg.coef_)  
# [ 2.60996757] [[-0.12759678  0.9144504 ]]

X_plot = np.linspace(-3, 3, 1000).reshape(-1, 1)
X_plot_poly = poly_features.fit_transform(X_plot)
y_plot = lin_reg.predict(X_plot_poly)
plt.plot(X_plot, y_plot, 'red')
plt.plot(X, y, 'b.')
plt.show()

第3行得到了训练后的参数，即多项式方程为h=-0.13x+0.91x^2+2.61h=−0.13x+0.91x2+2.61（结果中系数的顺序与𝑋中特征的顺序一致），如下图所示：

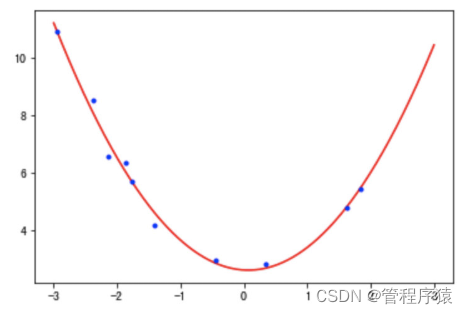
# 使用mse衡量其误差值:
y_pre = lin_reg.predict(X_poly)
mean_squared_error(y, y_pre)
# 0.07128562789085331

利用多项式回归，代价函数MSE的值下降到了0.07。

通过观察代码，可以发现训练多项式方程与直线方程唯一的差别是输入的训练集𝑋的差别。在训练直线方程时直接输入了𝑋的值，在训练多项式方程的时候，还添加了我们计算出来的x2这个“新特征”的值（由于x2完全是由x的值确定的，因此严格意义上来讲此时该模型只有一个特征x）。

此时有个非常有趣的问题：假如一开始得到的数据就是上面代码中"X_poly"的样子，且不知道x1与x2之间的关系。此时相当于我们有10个样本，每个样本具有x1,x2两个不同的特征。这时假设函数为：

直接按照二元线性回归方程来训练，也可以得到上面同样的结果（𝜃的值）。如果在相同情况下，收集到了新的数据，可以直接带入上面的方程进行预测。

唯一不同的是，我们不知道x2=x^2_1x2=x12这个隐含在数据内部的关系，所有也就无法画出上图中的这条曲线。一旦了解到了这两个特征之间的关系，数据的维度就从3维下降到了2维（包含截距项\theta_0θ0）。

3 持续降低训练误差与过拟合

在上面实现多项式回归的过程中，通过引入高阶项x2，训练误差从3.34下降到了0.07，减小了将近50倍。那么训练误差是否还有进一步下降的空间呢？

• 答案是肯定的，通过继续增加更高阶的项，训练误差可以进一步降低。通过尝试，当最高阶项为x12时，训练误差为3.87e-23，几乎等于0了。

下面是测试不同degree的过程：

# 定义模型训练函数
def try_degree(degree, X, y):
    poly_features_d = PolynomialFeatures(degree=degree, include_bias=False)
    X_poly_d = poly_features_d.fit_transform(X)
    lin_reg_d = LinearRegression()
    lin_reg_d.fit(X_poly_d, y)
    return {'X_poly': X_poly_d, 'intercept': lin_reg_d.intercept_, 'coef': lin_reg_d.coef_}

degree2loss_paras = []
for i in range(2, 20):
    paras = try_degree(i, X, y)

    # 自己实现预测值的求解
    h = np.dot(paras['X_poly'], paras['coef'].T) + paras['intercept']
    _loss = mean_squared_error(h, y)
    degree2loss_paras.append({'d': i, 'loss': _loss, 'coef': paras['coef'], 'intercept': paras['intercept']})

查看最小模型参数：

min_index = np.argmin(np.array([i['loss'] for i in degree2loss_paras]))
min_loss_para = degree2loss_paras[min_index]
print(min_loss_para)

# 输出结果
{'d': 12, 
 'loss': 3.8764202841976227e-23, 
 'coef': array([[ 1.17159189,  8.60674192, -4.91798703, -4.18378115,  3.79426131, -8.56026107, -6.94465715,  5.03891035,  4.08870088, -0.30369348, -0.6635493 , -0.11314395]]), 
 'intercept': array([1.63695924])}

对最小模型可视化展示：

X_plot = np.linspace(-3, 1.9, 1000).reshape(-1, 1)
poly_features_d = PolynomialFeatures(degree=min_loss_para['d'], include_bias=False)

X_plot_poly = poly_features_d.fit_transform(X_plot)
y_plot = np.dot(X_plot_poly, min_loss_para['coef'].T) + min_loss_para['intercept']


plt.plot(X_plot, y_plot, 'red', label="degree12")
plt.plot(X, y, 'b.', label="X")
plt.legend(loc='best')
plt.show()

此时函数图像穿过了每一个样本点，所有的训练样本都落在了拟合的曲线上，训练误差接近与0。 可以说是近乎完美的模型了。但是，这样的曲线与我们最开始数据的来源（一个二次方程加上一些随机误差）差异非常大。

如果从相同来源再取一些样本点，使用该模型预测会出现非常大的误差。类似这种训练误差非常小，但是新数据点的测试误差非常大的情况，就叫做模型的过拟合。过拟合出现时，表示模型过于复杂，过多考虑了当前样本的特殊情况以及噪音（模型学习到了当前训练样本非全局的特性），使得模型的泛化能力下降。

防止模型过拟合是机器学习领域里最重要的问题之一。鉴于该问题的普遍性和重要性，在满足要求的情况下，能选择简单模型时应该尽量选择简单的模型。

7.6.维灾难

1 什么是维灾难

随着维度的增加，分类器性能逐步上升，到达某点之后，其性能便逐渐下降

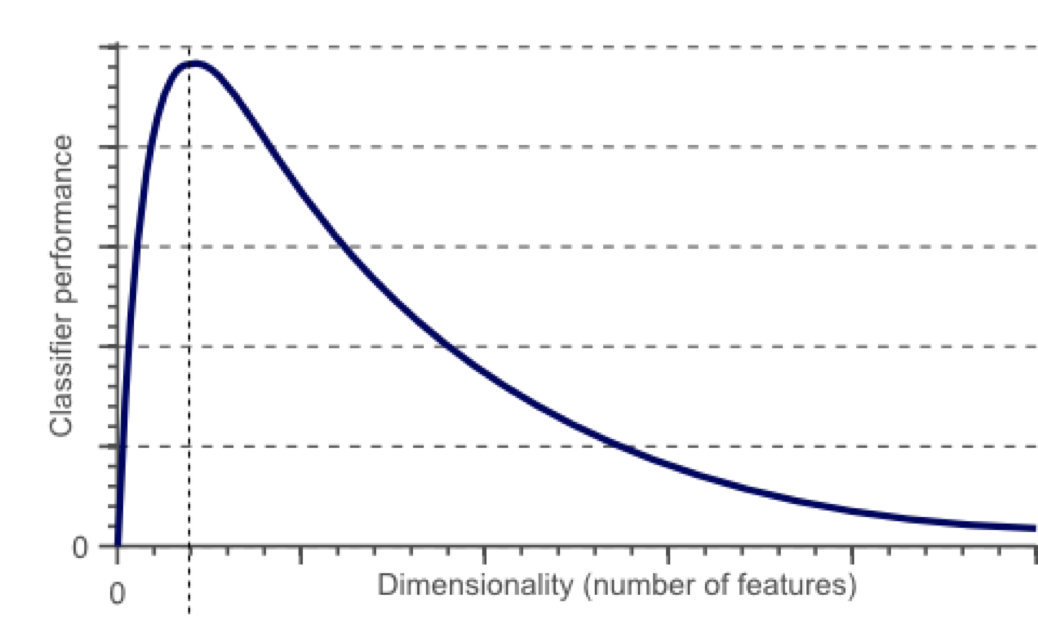
有一系列的图片，每张图片的内容可能是猫也可能是狗；我们需要构造一个分类器能够对猫、狗自动的分类。首先，要寻找到一些能够描述猫和狗的特征，这样我们的分类算法就可以利用这些特征去识别物体。猫和狗的皮毛颜色可能是一个很好的特征，考虑到红绿蓝构成图像的三基色，因此用图片三基色各自的平均值称得上方便直观。这样就有了一个简单的Fisher分类器：

If  0.5*red + 0.3*green + 0.2*blue > 0.6 : return cat;
    else return dog;

使用颜色特征可能无法得到一个足够准确的分类器，如果是这样的话，我们不妨加入一些诸如图像纹理(图像灰度值在其X、Y方向的导数dx、dy)，就有5个特征(Red、Blue、Green、dx、dy)来设计我们的分类器：

也许分类器准确率依然无法达到要求，加入更多的特征，比如颜色、纹理的统计信息等等，如此下去，可能会得到上百个特征。那是不是我们的分类器性能会随着特征数量的增加而逐步提高呢？答案也许有些让人沮丧，事实上，当特征数量达到一定规模后，分类器的性能是在下降的。

随着维度(特征数量)的增加，分类器的性能却下降了

2 维数灾难与过拟合

我们假设猫和狗图片的数量是有限的(样本数量总是有限的)，假设有10张图片，接下来我们就用这仅有的10张图片来训练我们的分类器。

增加一个特征，比如绿色，这样特征维数扩展到了2维：

增加一个特征后，我们依然无法找到一条简单的直线将它们有效分类

再增加一个特征，比如蓝色，扩展到3维特征空间：

在3维特征空间中，我们很容易找到一个分类平面，能够在训练集上有效的将猫和狗进行分类：

在高维空间中，我们似乎能得到更优的分类器性能。

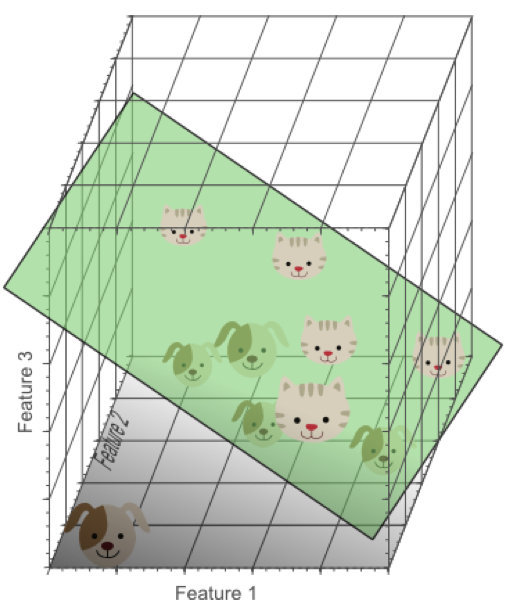
从1维到3维，给我们的感觉是：维数越高，分类性能越优。然而，维数过高将导致一定的问题：在一维特征空间下，我们假设一个维度的宽度为5个单位，这样样本密度为10/5=2;在2维特征空间下，10个样本所分布的空间大小25，这样样本密度为10/25=0.4;在3维特征空间下，10个样本分布的空间大小为125，样本密度就为10/125=0.08.

如果继续增加特征数量，随着维度的增加，样本将变得越来越稀疏，在这种情况下，也更容易找到一个超平面将目标分开。然而，如果我们将高维空间向低维空间投影，高维空间隐藏的问题将会显现出来：

过多的特征导致的过拟合现象：训练集上表现良好，但是对新数据缺乏泛化能力。

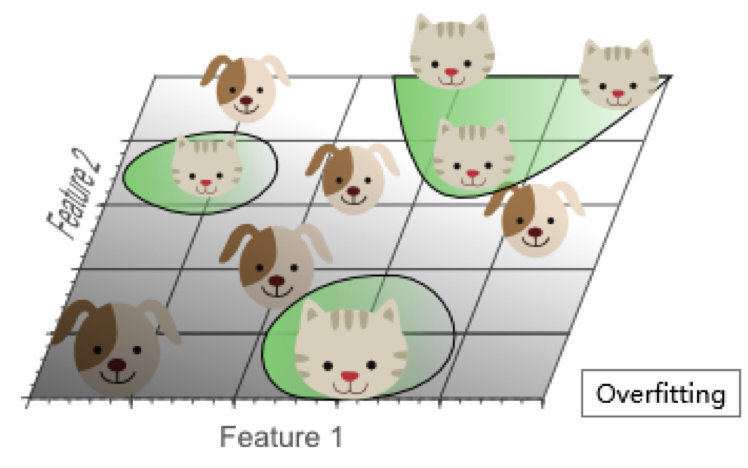
高维空间训练形成的线性分类器，相当于在低维空间的一个复杂的非线性分类器，这种分类器过多的强调了训练集的准确率甚至于对一些错误/异常的数据也进行了学习，而正确的数据却无法覆盖整个特征空间。为此，这样得到的分类器在对新数据进行预测时将会出现错误。这种现象称之为过拟合，同时也是维灾难的直接体现。

简单的线性分类器在训练数据上的表现不如非线性分类器，但由于线性分类器的学习过程中对噪声没有对非线性分类器敏感，因此对新数据具备更优的泛化能力。换句话说，通过使用更少的特征，避免了维数灾难的发生(也即避免了高维情况下的过拟合)

由于高维而带来的数据稀疏性问题：假设有一个特征，它的取值范围D在0到1之间均匀分布，并且对狗和猫来说其值都是唯一的，我们现在利用这个特征来设计分类器。如果我们的训练数据覆盖了取值范围的20%(e.g 0到0.2)，那么所使用的训练数据就占总样本量的20%。上升到二维情况下，覆盖二维特征空间20%的面积，则需要在每个维度上取得45%的取值范围。在三维情况下，要覆盖特征空间20%的体积，则需要在每个维度上取得58%的取值范围…在维度接近一定程度时，要取得同样的训练样本数量，则几乎要在每个维度上取得接近100%的取值范围，或者增加总样本数量，但样本数量也总是有限的。

如果一直增加特征维数，由于样本分布越来越稀疏，如果要避免过拟合的出现，就不得不持续增加样本数量。

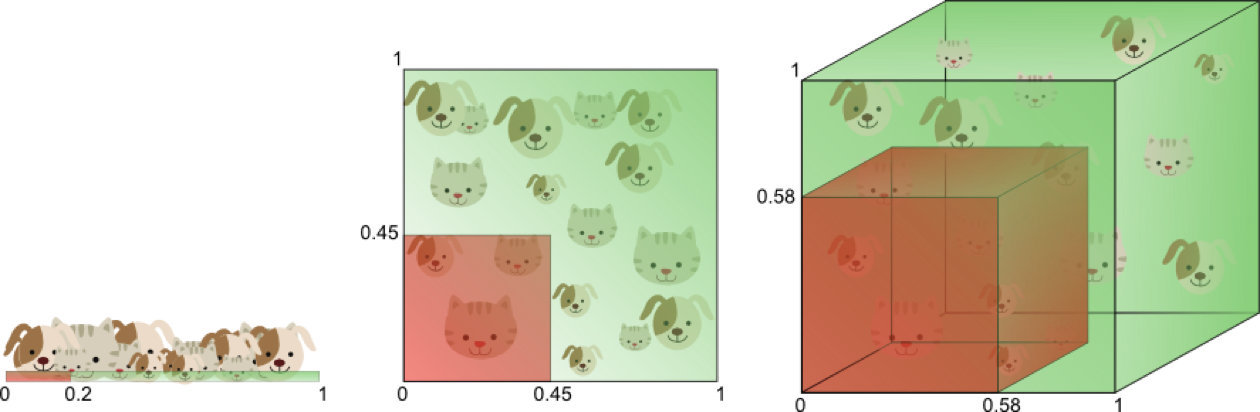
数据在高维空间的中心比在边缘区域具备更大的稀疏性，数据更倾向于分布在空间的边缘区域：

不属于单位圆的训练样本比搜索空间的中心更接近搜索空间的角点。这些样本很难分类，因为它们的特征值差别很大（例如，单位正方形的对角的样本）。

一个有趣的问题是，当我们增加特征空间的维度时，圆（超球面）的体积如何相对于正方形（超立方体）的体积发生变化。尺寸d的单位超立方体的体积总是1 ^ d = 1.尺寸d和半径0.5的内切超球体的体积可以计算为：

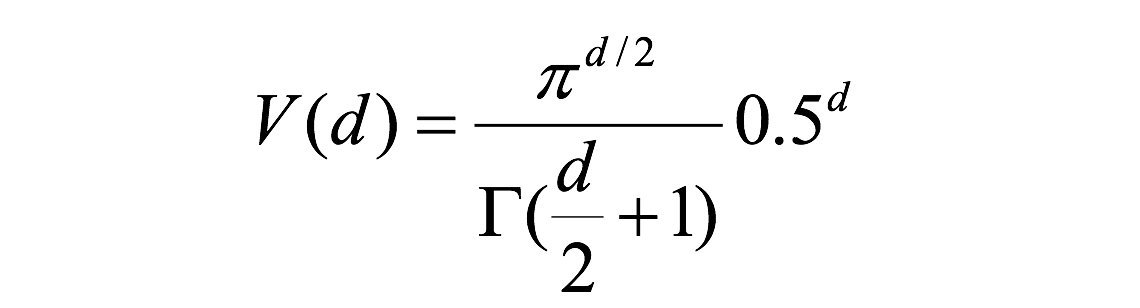
在高维空间中，大多数训练数据驻留在定义特征空间的超立方体的角落中。如前所述，特征空间角落中的实例比围绕超球体质心的实例难以分类。

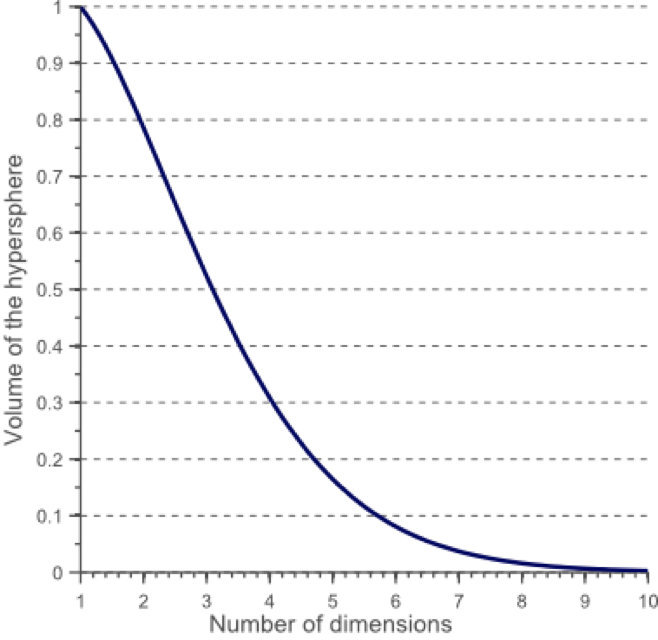
在高维空间中，大多数训练数据驻留在定义特征空间的超立方体的角落中。如前所述，特征空间角落中的实例比围绕超球体质心的实例难以分类：

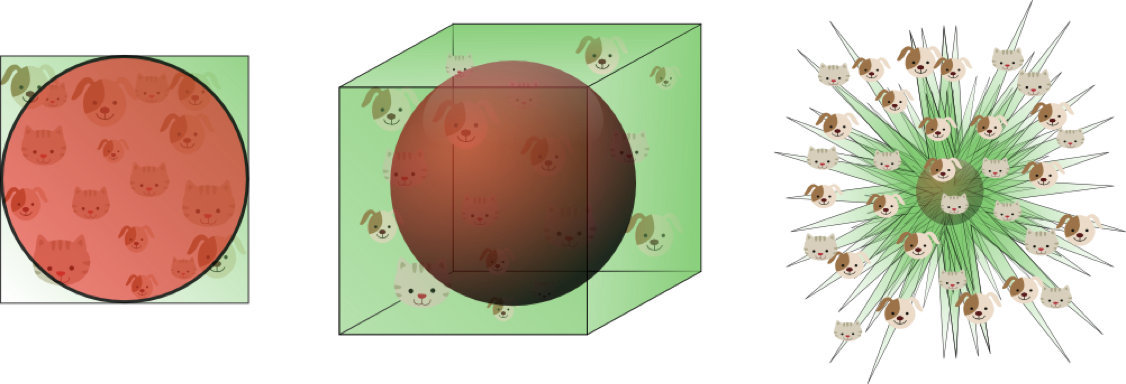
an 8D hypercube which has 2^8 = 256 corners

事实证明，许多事物在高维空间中表现得非常不同。 例如，如果你选择一个单位平方（1×1平方）的随机点，它将只有大约0.4％的机会位于小于0.001的边界（换句话说，随机点将沿任何维度“极端”这是非常不可能的）。 但是在一个10000维单位超立方体（1×1×1立方体，有1万个1）中，这个概率大于99.999999％。 高维超立方体中的大部分点都非常靠近边界。更难区分的是：如果你在一个单位正方形中随机抽取两个点，这两个点之间的距离平均约为0.52。如果在单位三维立方体中选取两个随机点，则平均距离将大致为0.66。但是在一个100万维的超立方体中随机抽取两点呢？那么平均距离将是大约408.25（大约1,000,000 / 6）！

非常违反直觉：当两个点位于相同的单位超立方体内时，两点如何分离？这个事实意味着高维数据集有可能非常稀疏：大多数训练实例可能彼此远离。当然，这也意味着一个新实例可能离任何训练实例都很远，这使得预测的可信度表现得比在低维度数据中要来的差。训练集的维度越多，过度拟合的风险就越大。

理论上讲，维度灾难的一个解决方案可能是增加训练集的大小以达到足够密度的训练实例。 不幸的是，在实践中，达到给定密度所需的训练实例的数量随着维度的数量呈指数增长。 如果只有100个特征（比MNIST问题少得多），那么为了使训练实例的平均值在0.1以内，需要比可观察宇宙中的原子更多的训练实例，假设它们在所有维度上均匀分布。

对于8维超立方体，大约98％的数据集中在其256个角上。结果，当特征空间的维度达到无穷大时，从采样点到质心的最小和最大欧几里得距离的差与最小距离本身只比趋于零：

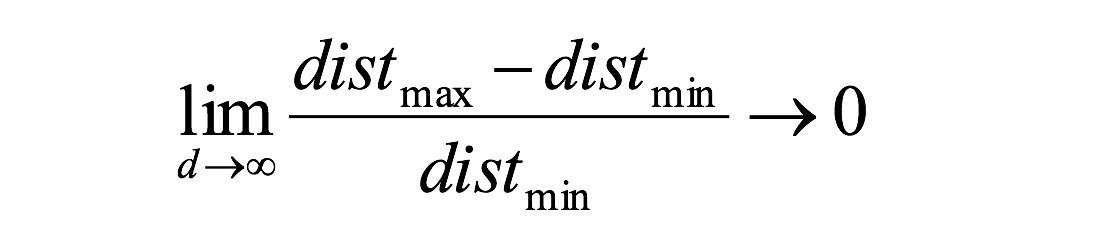
距离测量开始失去其在高维空间中测量的有效性,由于分类器取决于这些距离测量,因此在较低维空间中分类通常更容易，其中较少特征用于描述感兴趣对象。

如果理论无限数量的训练样本可用，则维度的诅咒不适用，我们可以简单地使用无数个特征来获得完美的分类。训练数据的大小越小，应使用的功能就越少。如果N个训练样本足以覆盖单位区间大小的1D特征空间，则需要N ^ 2个样本来覆盖具有相同密度的2D特征空间，并且在3D特征空间中需要N ^ 3个样本。换句话说，所需的训练实例数量随着使用的维度数量呈指数增长。

7.7.分类中解决类别不平衡问题

---

前面我们已经初步认识了，什么是类别不平衡问题。其实，在现实环境中，采集的数据（建模样本）往往是比例失衡的。比如网贷数据，逾期人数的比例是极低的（千分之几的比例）；奢侈品消费人群鉴定等。

1 类别不平衡数据集基本介绍

在这一节中，我们一起看一下，当遇到数据类别不平衡的时候，我们该如何处理。在Python中，有Imblearn包，它就是为处理数据比例失衡而生的。

• 安装Imblearn包

pip3 install imbalanced-learn

第三方包链接：https://pypi.org/project/imbalanced-learn/

• 创造数据集

from sklearn.datasets import make_classification
import matplotlib.pyplot as plt

#使用make_classification生成样本数据
X, y = make_classification(n_samples=5000, 
                           n_features=2,  # 特征个数= n_informative（） + n_redundant + n_repeated 
                           n_informative=2,  # 多信息特征的个数
                           n_redundant=0,   # 冗余信息，informative特征的随机线性组合
                           n_repeated=0,  # 重复信息，随机提取n_informative和n_redundant 特征 
                           n_classes=3,  # 分类类别
                           n_clusters_per_class=1,  # 某一个类别是由几个cluster构成的
                           weights=[0.01, 0.05, 0.94],  # 列表类型，权重比
                           random_state=0)

• 查看各个标签的样本

#查看各个标签的样本量
from collections import Counter
Counter(y)

# Counter({2: 4674, 1: 262, 0: 64})

• 数据集可视化

# 数据集可视化
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()

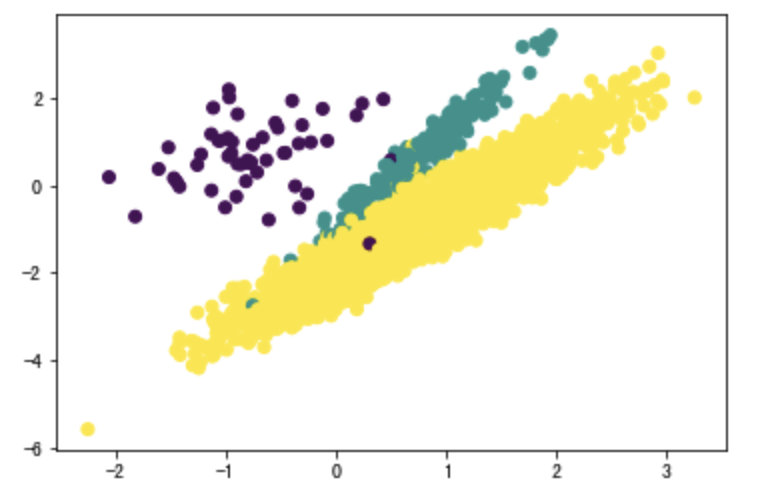
可以看出样本的三个标签中，1，2的样本量极少，样本失衡。下面使用imblearn进行过采样。

接下来，我们就要基于以上数据，进行相应的处理。

---

关于类别不平衡的问题，主要有两种处理方式：

• 过采样方法
  • 增加数量较少那一类样本的数量，使得正负样本比例均衡。
• 欠采样方法
  • 减少数量较多那一类样本的数量，使得正负样本比例均衡。

2 解决类别不平衡数据方法介绍

2.1 过采样方法

2.1.1 什么是过采样方法

对训练集里的少数类进行“过采样”（oversampling），即增加一些少数类样本使得正、反例数目接近，然后再进行学习。

2.1.2 随机过采样方法

随机过采样是在少数类

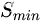
中随机选择一些样本，然后通过复制所选择的样本生成样本集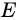
，将它们添加到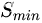
中来扩大原始数据集从而得到新的少数类集合

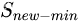
。新的数据集

• 通过代码实现随机过采样方法：

# 使用imblearn进行随机过采样
from imblearn.over_sampling import RandomOverSampler
ros = RandomOverSampler(random_state=0)
X_resampled, y_resampled = ros.fit_resample(X, y)
#查看结果
Counter(y_resampled)

#过采样后样本结果
# Counter({2: 4674, 1: 4674, 0: 4674})

# 数据集可视化
plt.scatter(X_resampled[:, 0], X_resampled[:, 1], c=y_resampled)
plt.show()

---

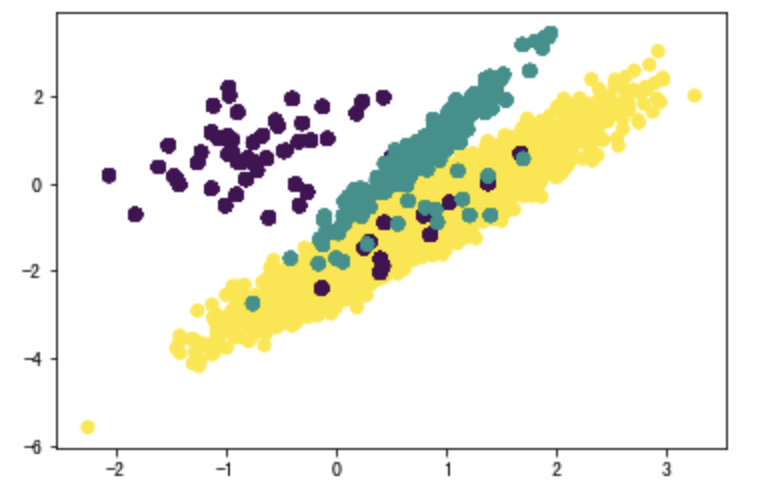
• 缺点：
  • 对于随机过采样，由于需要对少数类样本进行复制来扩大数据集，造成模型训练复杂度加大。
  • 另一方面也容易造成模型的过拟合问题，因为随机过采样是简单的对初始样本进行复制采样，这就使得学习器学得的规则过于具体化，不利于学习器的泛化性能，造成过拟合问题。

为了解决随机过采样中造成模型过拟合问题，又能保证实现数据集均衡的目的，出现了过采样法代表性的算法SMOTE算法。

2.1.3 过采样代表性算法-SMOTE

SMOTE全称是Synthetic Minority Oversampling即合成少数类过采样技术。

SMOTE算法是对随机过采样方法的一个改进算法，由于随机过采样方法是直接对少数类进行重采用，会使训练集中有很多重复的样本，容易造成产生的模型过拟合问题。而SMOTE算法的基本思想:

SMOTE算法合成新少数类样本的算法描述如下：

---

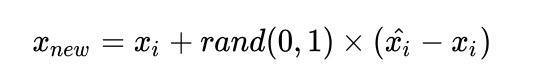
我们用图文表达的方式，再来描述一下SMOTE算法。

1. 先随机选定一个少数类样本
   。

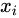
2. 找出这个少数类样本
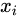
   的K个近邻（假设K=5），5个近邻已经被圈出。

3. 随机从这K个近邻中选出一个样本
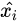
   （用绿色圈出来了）。

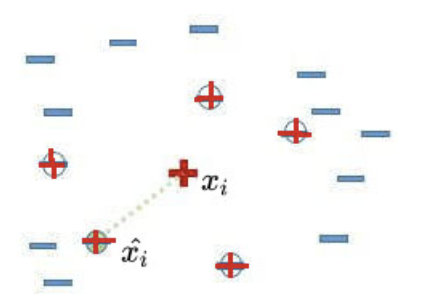
4)在少数类样本

和被选中的这个近邻样本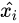
之间的连线上，随机找一点。这个点就是人工合成的新的样本点（绿色正号标出）。

SMOTE算法摒弃了随机过采样复制样本的做法，可以防止随机过采样中容易过拟合的问题，实践证明此方法可以提高分类器的性能。

• 代码实现：

# SMOTE过采样
from imblearn.over_sampling import SMOTE
X_resampled, y_resampled = SMOTE().fit_resample(X, y)
Counter(y_resampled)

# 采样后样本结果
# [(0, 4674), (1, 4674), (2, 4674)]

# 数据集可视化
plt.scatter(X_resampled[:, 0], X_resampled[:, 1], c=y_resampled)
plt.show()

2.2 欠采样方法

2.2.1 什么是欠采样方法

直接对训练集中多数类样本进行“欠采样”（undersampling），即去除一些多数类中的样本使得正例、反例数目接近，然后再进行学习。

2.2.2 随机欠采样方法

• 代码实现：

# 随机欠采样
from imblearn.under_sampling import RandomUnderSampler
rus = RandomUnderSampler(random_state=0)
X_resampled, y_resampled = rus.fit_resample(X, y)
Counter(y_resampled)

# 采样后结果
[(0, 64), (1, 64), (2, 64)]

# 数据集可视化
plt.scatter(X_resampled[:, 0], X_resampled[:, 1], c=y_resampled)
plt.show()

---

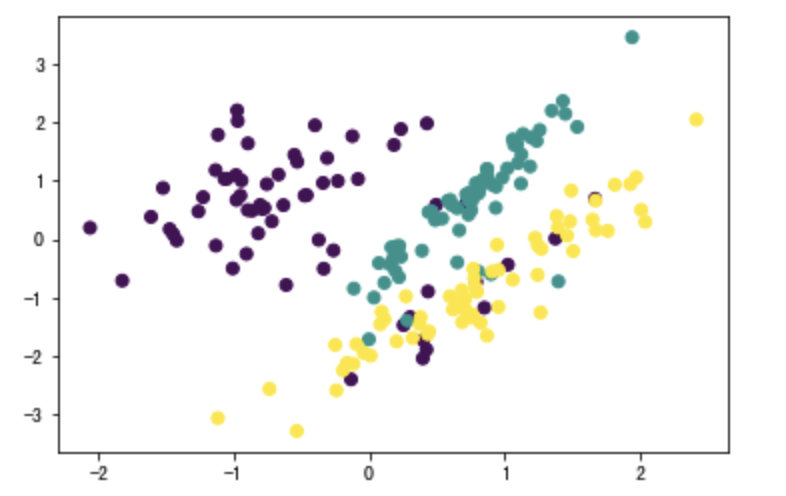
• 缺点：
  • 随机欠采样方法通过改变多数类样本比例以达到修改样本分布的目的，从而使样本分布较为均衡，但是这也存在一些问题。对于随机欠采样，由于采样的样本集合要少于原来的样本集合，因此会造成一些信息缺失，即将多数类样本删除有可能会导致分类器丢失有关多数类的重要信息。

---

官网链接：https://imbalanced-learn.readthedocs.io/en/stable/ensemble.html

7.8.向量与矩阵的范数

1.向量的范数

向量的1-范数：
; 各个元素的绝对值之和；

向量的2-范数：
每个元素的平方和再开平方根；

向量的无穷范数：

例：向量X=[2, 3, -5, -7] ，求向量的1-范数，2-范数和无穷范数。

向量X的1-范数：各个元素的绝对值之和 = 2+3+5+7 = 17=2+3+5+7=17；

向量X的2-范数：每个元素的平方和再开平方根；；

向量X的无穷范数：

（1）正无穷范数：向量的所有元素的绝对值中最大的；即X的正无穷范数为：7；

（2）负无穷范数：向量的所有元素的绝对值中最小的；即X的负无穷范数为：2；

2.矩阵的范数

设：向量 X \in R^nX∈R**n ，矩阵 A \in R^{n \times n}A∈R**n×n ，例如矩阵A为：

A=[2, 3, -5, -7;

   4, 6,  8, -4;

   6, -11, -3, 16];

（1）矩阵的1-范数（列模）：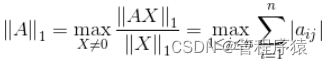
；矩阵的每一列上的元素绝对值先求和，再从中取个最大的，（列和最大)；即矩阵A的1-范数为：27

（2）矩阵的2-范数（谱模）：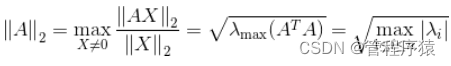
，其中\lambda_iλ**i为A^{TA*A**T**A*的特征值；矩阵A}TAATA的最大特征值开平方根。

（3）矩阵的无穷范数（行模）：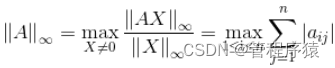
；矩阵的每一行上的元素绝对值先求和，再从中取个最大的，（行和最大)

---

原文链接：https://blog.csdn.net/zaishuiyifangxym/article/details/81673491

7.9. 无偏估计

1.如何理解无偏估计

无偏估计：就是我认为所有样本出现的概率一样。

假如有N种样本我们认为所有样本出现概率都是1/N。然后根据这个来计算数学期望。此时的数学期望就是我们平常讲的平均值。

数学期望本质就是平均值

2.无偏估计为何叫做“无偏”？它要“估计”什么？

首先回答第一个问题：它要“估计”什么？

• 它要估计的是整体的数学期望（平均值）。

第二个问题：那为何叫做无偏？有偏是什么？

• 假设这个是一些样本的集合:X=x_1, x_2, x_3,…,x_NX=x1,x2,x3,…,x**N 我们根据样本估计整体的数学期望（平均值）。

• 因为正常求期望是加权和，什么叫加权和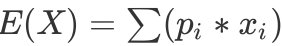这个就叫加权和。每个样本出现概率不一样，概率大的乘起来就大，这个就产生偏重了（有偏估计）。

• 但是，但是我们不知道某个样本出现的概率啊。比如你从别人口袋里面随机拿了3张钞票。两张是十块钱，一张100元，然后你想估计下他口袋里的剩下的钱平均下来每张多少钱（估计平均值）。

• 然后呢？

• 无偏估计计算数学期望

  就是认为所有样本出现概率一样大，没有看不起哪个样本。

  • 回到求钱的平均值的问题。无偏估计我们认为每张钞票出现概率都是1/2（因为只出现了10和100这两种情况，所以是1/2。如果是出现1 10 100三种情况，每种情况概率则是1/3。
  • 哪怕拿到了两张十块钱，我还是认为十块钱出现的概率和100元的概率一样。不偏心。所以无偏估计，所估计的别人口袋每张钱的数学期望（平均值）=10 1/2+100 1/2。

• 有偏估计那就是偏重那些出现次数多的样本。认为样本的概率是不一样的。

  • 我出现了两次十块钱，那么我认为十块钱的概率是2/3，100块钱概率只有1/3. 有偏所估计的别人口袋每张钱的数学期望（平均值）=10 2/3+100 1/3。

3.为何要用无偏估计？

因为现实生活中我不知道某个样本出现的概率啊，就像骰子，我不知道他是不是加过水银。

-SLV2PAhu-1667062043351)]；矩阵的每一行上的元素绝对值先求和，再从中取个最大的，（行和最大)

---

原文链接：https://blog.csdn.net/zaishuiyifangxym/article/details/81673491

7.9. 无偏估计

1.如何理解无偏估计

无偏估计：就是我认为所有样本出现的概率一样。

假如有N种样本我们认为所有样本出现概率都是1/N。然后根据这个来计算数学期望。此时的数学期望就是我们平常讲的平均值。

数学期望本质就是平均值

2.无偏估计为何叫做“无偏”？它要“估计”什么？

首先回答第一个问题：它要“估计”什么？

• 它要估计的是整体的数学期望（平均值）。

第二个问题：那为何叫做无偏？有偏是什么？

• 假设这个是一些样本的集合:X=x_1, x_2, x_3,…,x_NX=x1,x2,x3,…,x**N 我们根据样本估计整体的数学期望（平均值）。

• 因为正常求期望是加权和，什么叫加权和[外链图片转存中…(img-XXQrws8J-1667062043352)]这个就叫加权和。每个样本出现概率不一样，概率大的乘起来就大，这个就产生偏重了（有偏估计）。

• 但是，但是我们不知道某个样本出现的概率啊。比如你从别人口袋里面随机拿了3张钞票。两张是十块钱，一张100元，然后你想估计下他口袋里的剩下的钱平均下来每张多少钱（估计平均值）。

• 然后呢？

• 无偏估计计算数学期望

  就是认为所有样本出现概率一样大，没有看不起哪个样本。

  • 回到求钱的平均值的问题。无偏估计我们认为每张钞票出现概率都是1/2（因为只出现了10和100这两种情况，所以是1/2。如果是出现1 10 100三种情况，每种情况概率则是1/3。
  • 哪怕拿到了两张十块钱，我还是认为十块钱出现的概率和100元的概率一样。不偏心。所以无偏估计，所估计的别人口袋每张钱的数学期望（平均值）=10 1/2+100 1/2。

• 有偏估计那就是偏重那些出现次数多的样本。认为样本的概率是不一样的。

  • 我出现了两次十块钱，那么我认为十块钱的概率是2/3，100块钱概率只有1/3. 有偏所估计的别人口袋每张钱的数学期望（平均值）=10 2/3+100 1/3。

3.为何要用无偏估计？

因为现实生活中我不知道某个样本出现的概率啊，就像骰子，我不知道他是不是加过水银。

所以我们暂时按照每种情况出现概率一样来算。