E - Sugoroku 4 【概率dp】

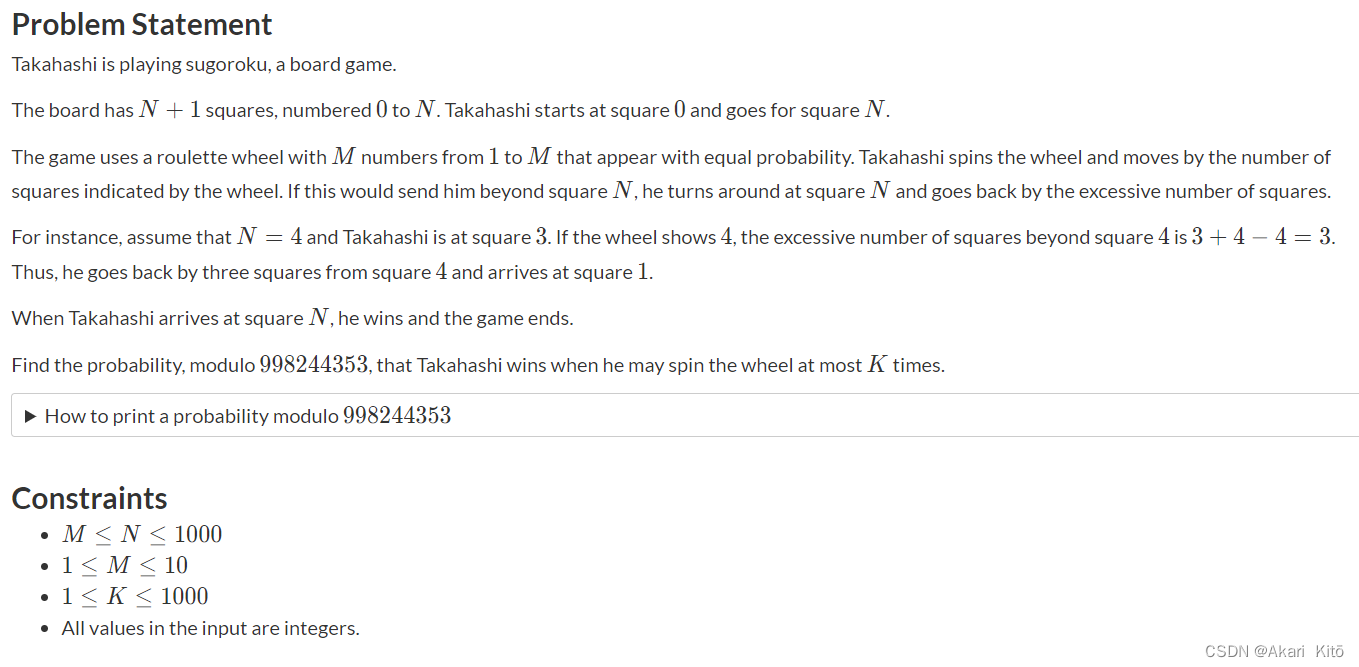
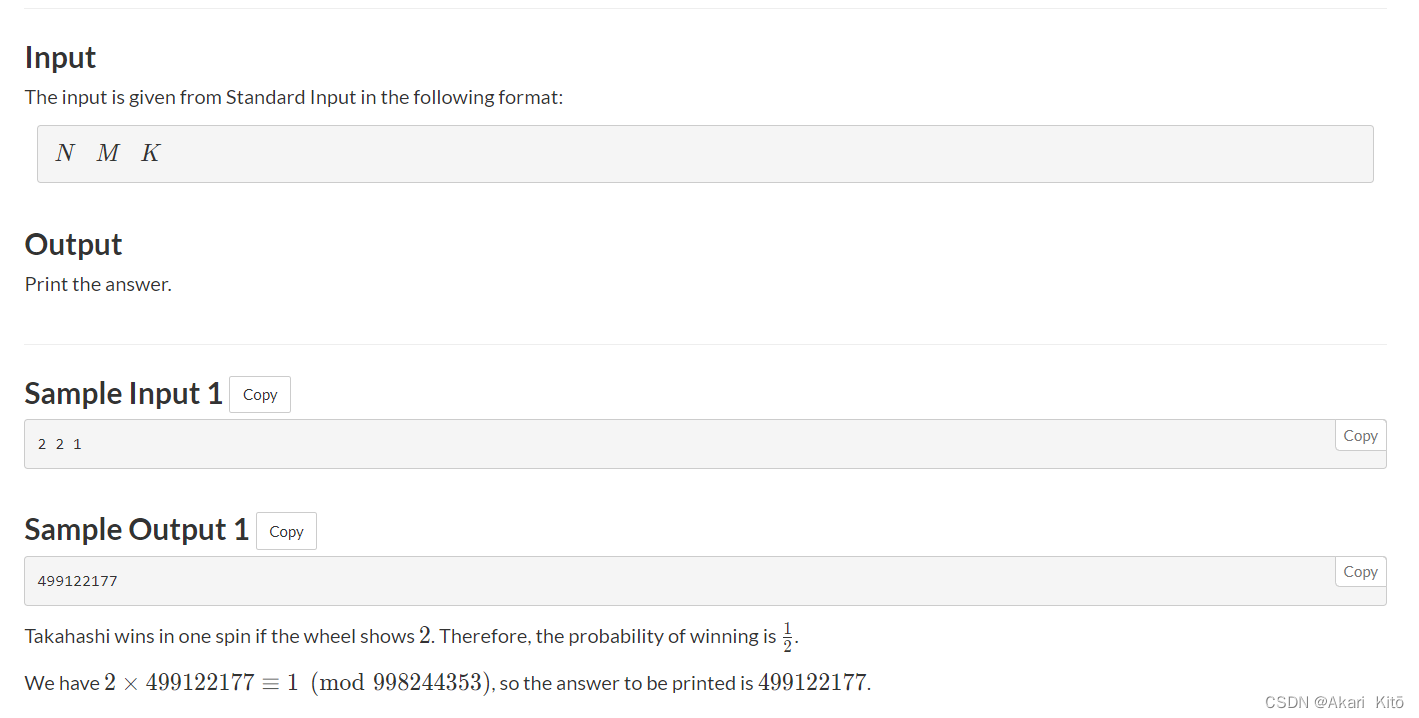
题意：
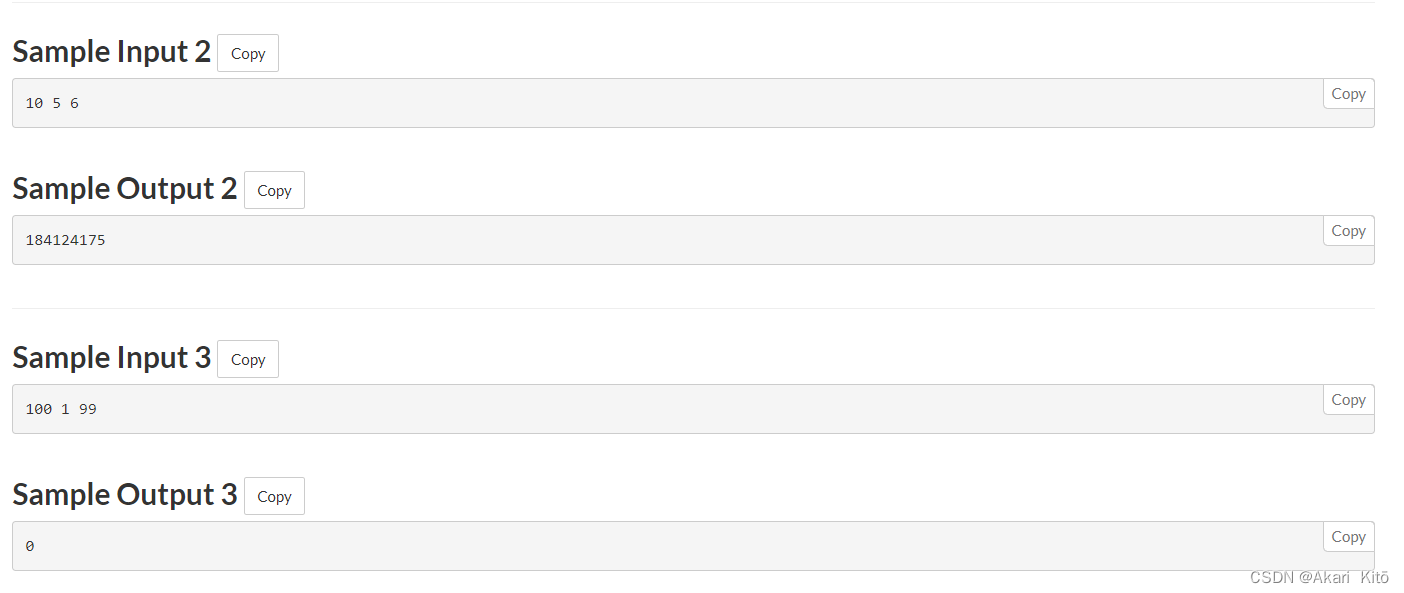
对于每个样例，读入n，m，k。
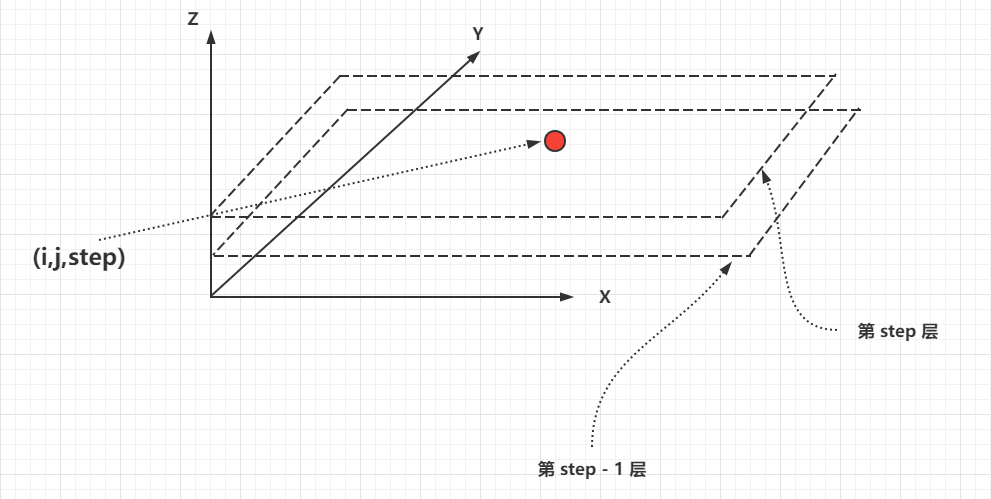
一维数轴，你现在在0这个点上，目标是到达n这个点，你有k次掷骰子的机会，每次可能等概率的掷出1~m的任意一个数字，之后你可以向前走对应的步数（如果会大于n，到达n后会向左走完剩余的步数，但是下次依旧是向右走），问你k次内，到达n的概率。
分析：
数据范围不大，因此可以暴力dp
dp[i][j]表示i轮后，位于位置j的概率。
转移时，建议枚举上一轮所在位置，因为这个的概率一定是$1/m$，如果枚举的是这一轮的位置，之后通过枚举点数确定上一轮的位置的话，概率可能不为$1/m$。
AC代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

ll dp[1005][1005];
ll n, m, k;
const ll mod = 998244353;
ll ni;

ll pow_mod(ll a, ll n)
{
    ll ans = 1;
    a %= mod;
    while(n)
    {
        if(n & 1) ans = (ans * a) % mod;
        a = (a * a) % mod;
        n >>= 1;
    }
    return ans;
}


int main()
{
    cin >> n >> m >> k;

    ni = pow_mod(m, mod - 2);

    dp[0][0] = 1;
    for(int i = 0; i < k; ++i)
    {
        for(int j = 0; j < n; ++j)
        {
            for(int p = 1; p <= m; ++p)
            {
                if(j + p <= n) dp[i + 1][j + p] = (dp[i + 1][j + p] + dp[i][j] * ni) % mod;
                else dp[i + 1][2 * n - p - j] = (dp[i + 1][2 * n - p - j] + dp[i][j] * ni) % mod;
            }
        }
    }

    ll ans = 0;

    for(int i = 1; i <= k; ++i) ans = (ans + dp[i][n]) % mod;
    printf("%lld\n", ans);

    return 0;
}

F - Erase Subarrays 【dp】

题意：
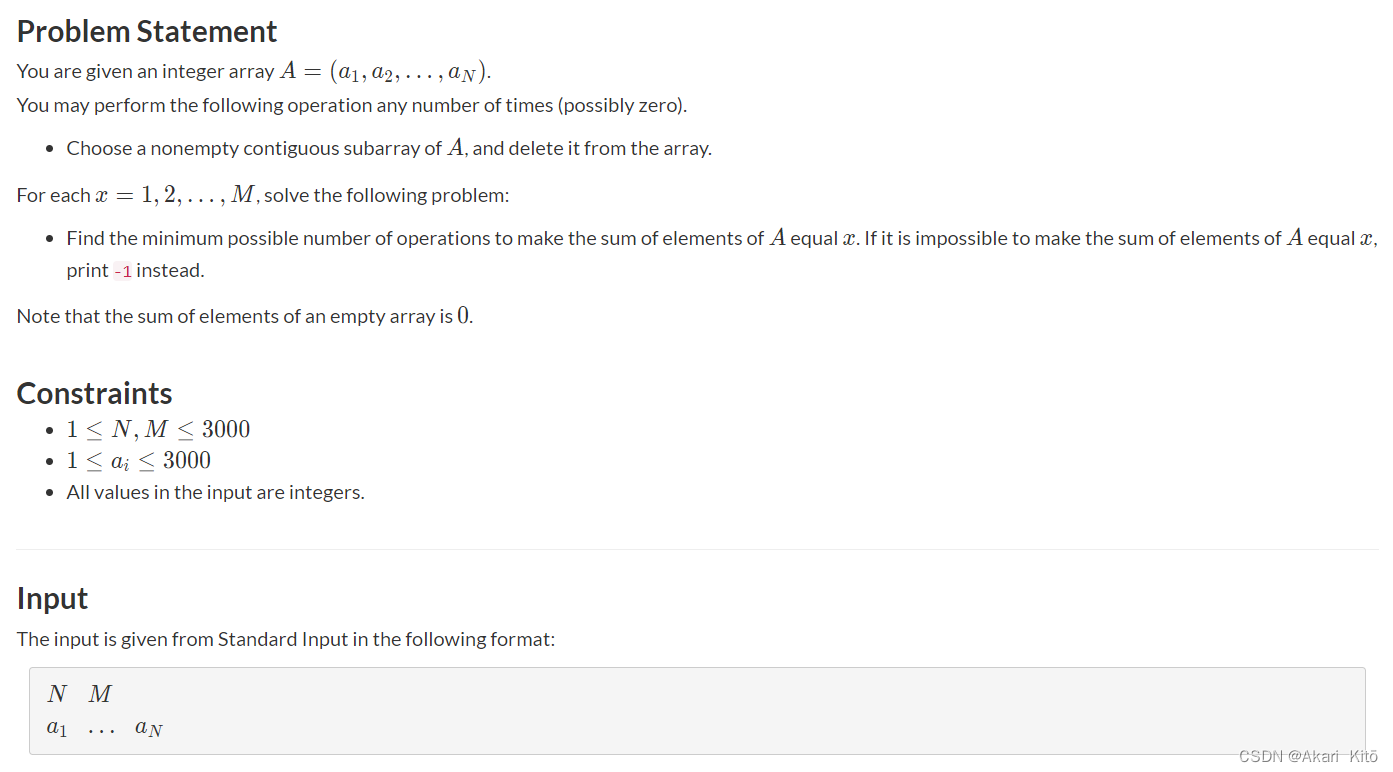
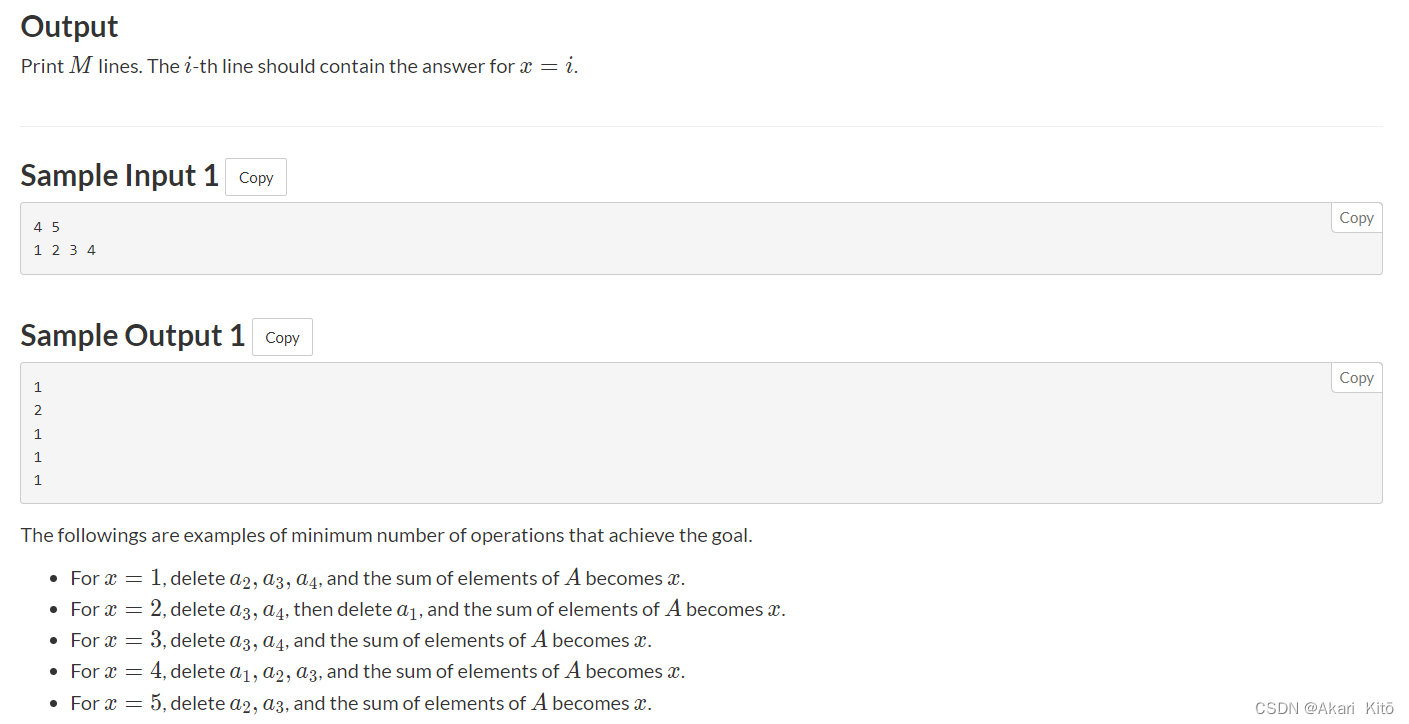
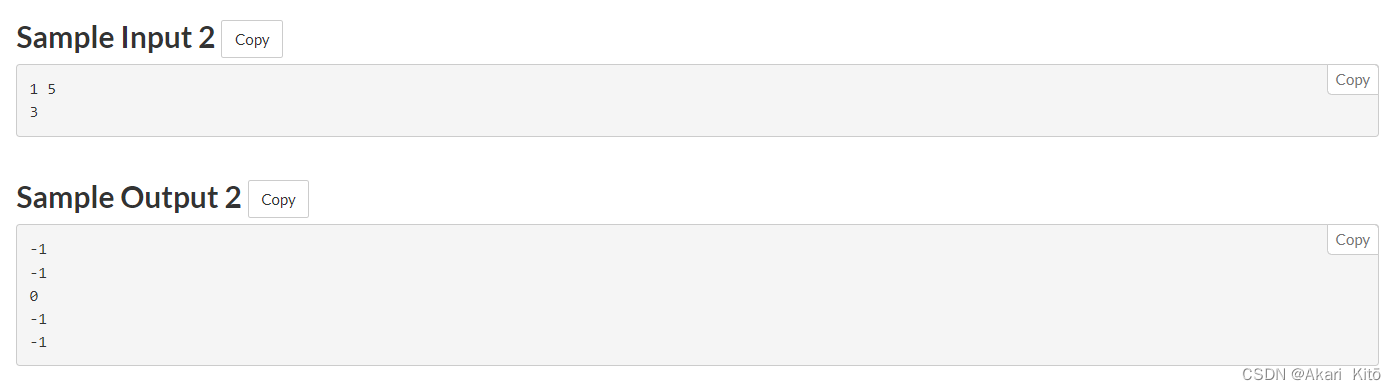
先输入n和m。之后n个数字表示数组a，你可以进行的操作是，删除数组a的任意一个子区间，你可以进行任意次。问你使得删除后的a数组的元素和等于$i$时的最小操作次数是多少$(1<=i<=m)$，不存在输出-1。
分析：
dp[i][j][0/1]表示第i位选或者不选是，区间$1-i$经过操作后凑出j的最小操作数，另外令a[0]=0,则dp[0][0][1] = 0,dp[0][0][0] = inf。其余状态初识化为inf。
AC代码：

#include <bits/stdc++.h>

using namespace std;

const int inf = 0x3f3f3f3f;
int n, m, mi;
int ar[3005];
int dp[3005][3005][3];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);

    memset(dp, 0x3f, sizeof(dp));

    dp[0][0][1] = 0;

    for(int i = 1; i <= n; ++i)
    {
        for(int j = 0; j <= m; ++j)
        {
            dp[i][j][0] = min(dp[i - 1][j][1], dp[i - 1][j][0]);
            if(j - ar[i] >= 0) dp[i][j][1] = min(dp[i - 1][j - ar[i]][0] + 1, dp[i - 1][j - ar[i]][1]);
            //cout << i << ' ' << j << ' ' << dp[i][j][0] << ' ' << dp[i][j][1] << '\n';
        }
    }

    for(int i = 1; i <= m; ++i)
    {
        mi = min(dp[n][i][0] + 1, dp[n][i][1]);
        if(mi >= inf) printf("-1\n");
        else printf("%d\n", mi);
    }

    return 0;
}