基于LSTM、GRU和RNN的交通时间序列预测（Python）

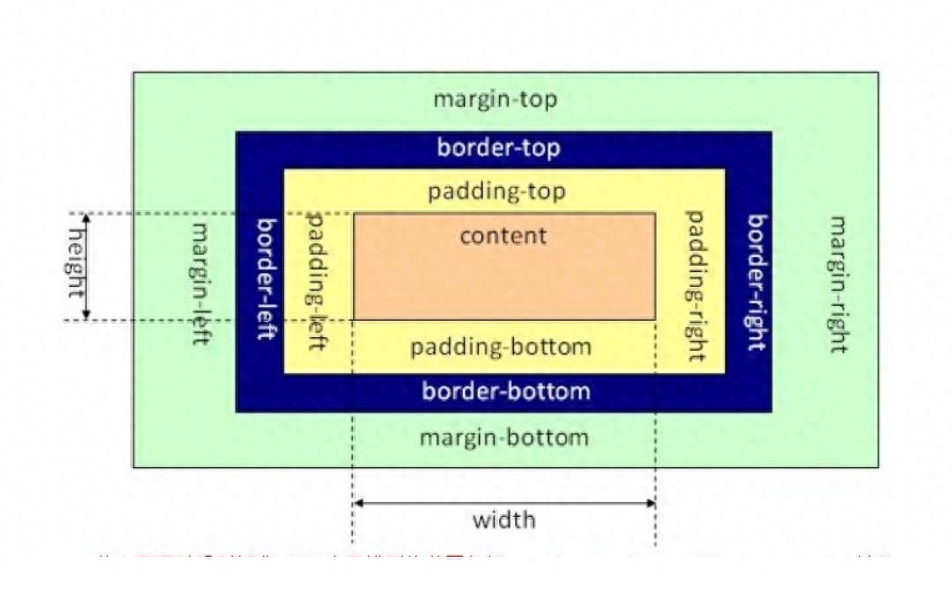
近年来，人工智能技术的发展推动了智慧交通领域的进步，交通流预测日益成为研究热点之一。交通流预测是基于历史的交通数据对未来时段的交通流状态参数进行预测。作为交通流状态的直接反映，交通流参数的预测结果可以直接应用于 ATIS 和ATMS 中，为交通管理者实施管控、诱导措施提供有效参考。

根据基础数据的时间窗和预测步长，交通流预测存在长时、短时预测之分。长时预测的预测步长往往是一小时或更长的时间，预测结果常应用于交通规划、交通影响评价。短时预测的预测步长一般在 15 分钟以内（如：2 分钟、5 分钟），预测结果常作为实时交通管控和交通诱导的有效参考，也更具研究价值，预测方法可分为模型驱动方法和数据驱动方法两大类。

交通流参数预测的模型驱动方法主要以动态交通流仿真模型为代表，如DynaMIT-P，DynaSmart-X，Visum-online 等。数据驱动方法主要通过数理分析、机器学习等方法，以历史交通数据为主要研究对象进行预测，该方法从数据本身出发，避免了分析复杂的交通系统，且运算效率更适用于实时的在线运行。数据驱动的交通流预测方法可分为线形预测方法、非线性预测方法和智能预测方法三类。

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import numpy as np
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
from models import LSTMModel, RNNModel, GRUModel, SimpleTransformerModel
import pandas as pd
import matplotlib.pyplot as plt




def train_model(model, train_inputs, train_labels, learning_rate, epochs, batch_size=64):
    # Wrap training data and labels into TensorDataset and use DataLoader
    train_dataset = TensorDataset(train_inputs, train_labels)
    train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)


    # Define loss function and optimizer
    criterion = nn.MSELoss()
    optimizer = optim.AdamW(model.parameters(), lr=learning_rate)


    # Train the model
    for epoch in range(epochs):
        model.train()
        running_loss = 0.0
        for inputs, labels in train_loader:
            optimizer.zero_grad()
            outputs = model(inputs)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
            running_loss += loss.item()


        # Print average loss after each epoch
        print(f'Epoch {epoch+1}, Loss: {running_loss/len(train_loader)}')




def evaluate_model(model, test_inputs, test_labels, means, stds):
    model.eval()
    with torch.no_grad():
        predictions = model(test_inputs)
        predictions = predictions.squeeze().detach().numpy()
        test_labels = test_labels.squeeze().detach().numpy()


        predictions = predictions * stds.reshape(-1) + means.reshape(-1)
        # Initialize lists to store evaluation metrics
        rmses = []
        maes = []
        mapes = []


        # Define a threshold to filter out samples with near-zero true values
        threshold = 1e-6


        # Calculate metrics for each dimension of test_labels
        for i in range(test_labels.shape[1]):
            true = test_labels[:, i]
            pred = predictions[:, i]
            rmse = math.sqrt(mean_squared_error(true, pred))
            mae = mean_absolute_error(true, pred)


            # Calculate MAPE only for samples with true values above the threshold
            valid_indices = true > threshold
            valid_true = true[valid_indices]
            valid_pred = pred[valid_indices]
            if len(valid_true) > 0:
                mape = np.mean(np.abs((valid_true - valid_pred) / valid_true)) * 100
            else:
                mape = float('nan')


            rmses.append(rmse)
            maes.append(mae)
            mapes.append(mape)


        # Create a DataFrame to store and display evaluation metrics
        metrics_df = pd.DataFrame({
            'RMSE': rmses,
            'MAE': maes,
            'MAPE': mapes
        }, index=[f'Time Step {i + 1}' for i in range(test_labels.shape[1])])


        print(metrics_df)
        return metrics_df




def plot_predictions(model, inputs, labels, means, stds, vis_len, vis_step):
    model.eval()
    with torch.no_grad():
        # Obtain the predictions
        predictions = model(inputs[:vis_len]).squeeze().detach().numpy()
        # Denormalize the predictions and actual values
        predictions = predictions * stds.reshape(-1) + means.reshape(-1)
        predictions = predictions[:, vis_step - 1]
        actuals = labels[:vis_len, vis_step - 1].squeeze().detach().numpy()


    # Plot the graph
    plt.figure(figsize=(10, 6))
    plt.plot(predictions, label=f'Prediction (Step {vis_step})', color='red', linewidth=2, linestyle='-')
    plt.plot(actuals, label='Actual', color='black', linewidth=2, linestyle='--')
    plt.title('Predictions vs Actual')
    plt.xlabel('Time')
    plt.ylabel('Number of vehicles')
    plt.legend()
    plt.savefig('visualisation/predictions_vs_actual.png', dpi=300)




if __name__ == "__main__":
    # a. Load data
    file_path = 'data/'
    month = 1
    target = "Observations"
    input_seq_len = 12
    output_seq_len = 6
    file_name = f'traffic_data_M{month}_{target}_IN{input_seq_len}_OUT{output_seq_len}.npz'
    data = np.load(file_path + file_name)
    train_inputs = torch.Tensor(data['train_inputs'])
    train_labels = torch.Tensor(data['train_labels'])
    test_inputs = torch.Tensor(data['test_inputs'])
    test_labels = torch.Tensor(data['test_labels'])
    means = data['means']
    stds = data['stds']


    # b. Construct model
    input_dim = 1  # Default number of features is 1
    hidden_dim = 32  # hidden layer dimension
    output_seq_len = 6  # Output dimension
    model = LSTMModel(input_dim, hidden_dim, output_seq_len)
    #model = RNNModel(input_dim, hidden_dim, output_seq_len)
    #model = GRUModel(input_dim, hidden_dim, output_seq_len)


    # c. Train the model
    learning_rate = 0.005
    epochs = 20
    train_model(model, train_inputs, train_labels, learning_rate, epochs)


    # d. Evaluate the model
    evaluate_model(model, test_inputs, test_labels, means, stds)


    # e. Plot model prediction results
    vis_len = 100 # Length of time for visualization
    vis_step = 6 # Prediction step number for visualization
    plot_predictions(model, test_inputs, test_labels, means, stds, vis_len, vis_step)
import torch
import torch.nn as nn
import torch.nn.functional as F
import math




class RNNModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_seq_len):
        super(RNNModel, self).__init__()
        self.rnn = nn.RNN(input_dim, hidden_dim, batch_first=True)
        self.fc = nn.Linear(hidden_dim, output_seq_len)


    def forward(self, x):
        # x shape: (batch_size, seq_length, input_dim)
        x, _ = self.rnn(x)
        # Select the last time step's output
        x = x[:, -1, :]
        x = self.fc(F.relu(x))
        return x




class GRUModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_seq_len):
        super(GRUModel, self).__init__()
        self.rnn = nn.GRU(input_dim, hidden_dim, batch_first=True)
        self.fc = nn.Linear(hidden_dim, output_seq_len)


    def forward(self, x):
        # x shape: (batch_size, seq_length, input_dim)
        x, _ = self.rnn(x)
        # Select the last time step's output
        x = x[:, -1, :]
        x = self.fc(F.relu(x))
        return x




class LSTMModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_seq_len):
        super(LSTMModel, self).__init__()
        self.lstm = nn.LSTM(input_dim, hidden_dim, batch_first=True)
        self.fc = nn.Linear(hidden_dim, output_seq_len)  # Output dim remains 1 since we're predicting one step at a time


    def forward(self, x):
        x, (hn, cn) = self.lstm(x)
        # Assuming x is of shape (batch_size, seq_length, hidden_dim)
        # We take the output of the last time step and repeat it output_seq_len times
        x = x[:, -1, :]
        # Now pass each time step output through the fully connected layer
        x = self.fc(F.relu(x))
        return x




class TransformerModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_seq_len, nhead=2, num_encoder_layers=1):
        super(TransformerModel, self).__init__()
        self.encoder_layer = nn.TransformerEncoderLayer(d_model=input_dim, nhead=nhead, dim_feedforward=hidden_dim)
        self.transformer_encoder = nn.TransformerEncoder(self.encoder_layer, num_layers=num_encoder_layers)
        self.fc = nn.Linear(input_dim, output_seq_len)


    def forward(self, x):
        # x shape: (seq_length, batch_size, input_dim)
        x = x.permute(1, 0, 2)  # Transformer expects (seq_length, batch_size, input_dim)
        x = self.transformer_encoder(x)
        # Select the last time step's output
        x = x[-1, :, :]
        x = self.fc(x)
        return x




class SimpleTransformerModel(nn.Module):
    def __init__(self, input_dim, d_model, nhead, num_encoder_layers, output_seq_len):
        super(SimpleTransformerModel, self).__init__()
        self.d_model = d_model
        self.input_embedding = nn.Linear(input_dim, d_model)  # 将输入映射到较高维度
        self.pos_encoder = PositionalEncoding(d_model)
        encoder_layers = nn.TransformerEncoderLayer(d_model=d_model, nhead=nhead, dim_feedforward=d_model * 4)
        self.transformer_encoder = nn.TransformerEncoder(encoder_layer=encoder_layers, num_layers=num_encoder_layers)
        self.fc_out = nn.Linear(d_model, output_seq_len)  # 假设输出序列长度固定


    def forward(self, src):
        src = self.input_embedding(src) * math.sqrt(self.d_model)
        src = self.pos_encoder(src)
        src = src.permute(1, 0, 2)  # 转换为Transformer期望的格式
        output = self.transformer_encoder(src)
        output = output.permute(1, 0, 2)  # 转换回(batch_size, seq_len, features)
        output = self.fc_out(output[:, -1, :])  # 只取序列的最后一步
        return output


class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)


        position = torch.arange(max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
        pe = torch.zeros(max_len, d_model)
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0).transpose(0, 1)
        self.register_buffer('pe', pe)


    def forward(self, x):
        x = x + self.pe[:x.size(0), :]
        return self.dropout(x)



完整代码：https://mbd.pub/o/bread/mbd-ZZ6VmJly