x |（x+1）去掉从右开始的第一个0

a^a=0，异或遵循交换律，即只要存在偶数个a，这部分结果为0.

a^0=a  与0异或为本身

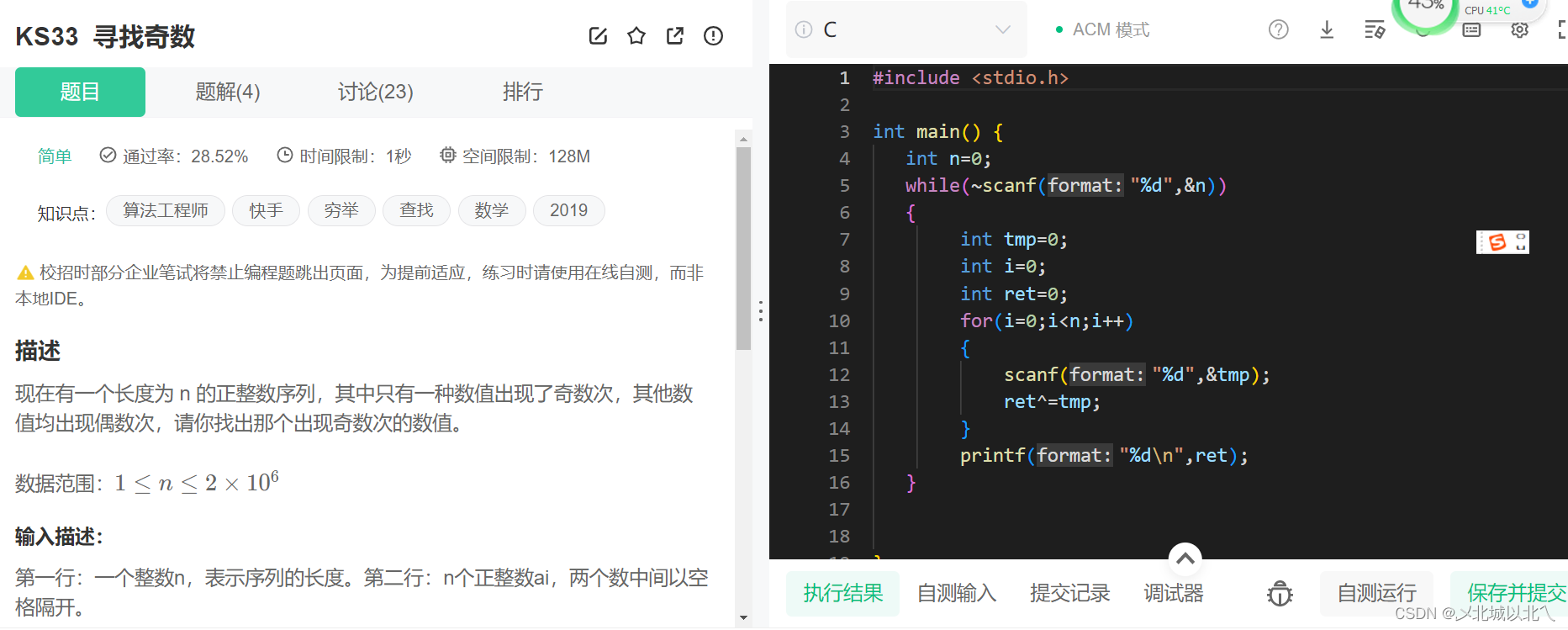
寻找奇数_牛客题霸_牛客网

不用加减乘除做加法_牛客题霸_牛客网

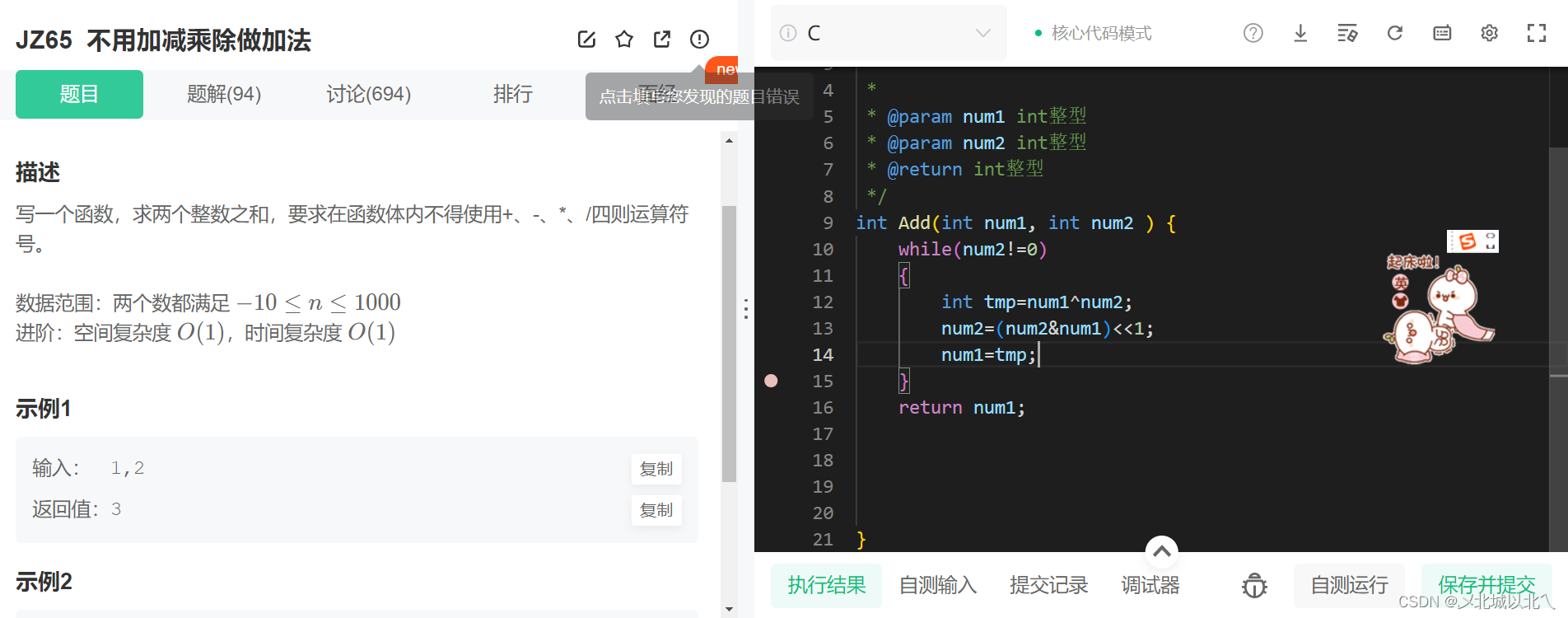
二进制进行加法运算时与十进制的思路是一致的，第一部分是不进位部分相加，第二部分是拿到进位的大小，然后将两部分相加。

例如：计算15+07时，第一部分为12，第二部分为10，两部分相加为22.

由于二进制只有0、1两种数字，可以不使用加法，而是通过位运算实现逻辑上的相加。

例如：我们实现5+7,  5:  0101        7：  0111

第一部分：不考虑进位时，相加得到 0010，拆开来看，两个0还是0，一个0一个1是1，两个1是0，即相异时为1，因此可以使用按位异或操作符^     得到0010也就是2

第二部分：考虑进位的部分，相加得到0101，然后<<1得到1010，只有两个都为1时才为1，然后左移进行进位，因此可使用按位与操作符&，   得到1010也就是10

经过上面两步，我们将5+7转换为了2+10，此时我们发现还需要继续进行加法操作，于是我们重复上述两个部分的操作。

2： 0010      10：  1010

第一部分： 1000即8

第二部分： 0100即4

转换为8+4，继续转换

8:  1000    4:  0100

第一部分：1100即12

第二部分：0000即0

当第二部分需要进位的部分为0时，我们的加法过程就结束了，第一部分就是相加后的最终结果。

int Add(int num1, int num2 ) {
    while(num2!=0)
    {
        int tmp=num1^num2;
        num2=(num2&num1)<<1;
        num1=tmp;
    }    
    return num1;
}

   num1^num2求的是第一部分，(num1&num2)<<1求的是第二部分，第二部分为0时结束。这里我用了tmp来接收第一部分的值，防止影响第二部分值的计算，也可以创建两个变量，使得逻辑更加清晰。

int main()
{
	int num1 = 0;
	int num2 = 0;
	while (num2 != 0)
	{
		int tmp1=num1^ num2;
		int tmp2 = (num1 & num2) << 1;
		num1 = tmp1;
		num2 = tmp2;
	}
}