目录
低通与带通信号的抽样定理:
模拟信号数字编码的基本概念:
模拟信号的抽样:
低通信号的理想抽样:
低通采样定理:
采样方式:
冲激采样示例:
低通信号的自然抽样:
带通抽样定理:
模拟信号的量化方法:
标量量化:
标量量化的量化方式与量化误差:
标量量化的量化噪声:
标量量化的过载噪声:
标量量化的信噪比:
矢量量化:
均匀量化:
非均匀量化:
对数量化:
A 率对数压缩变换:
µ率对数压缩变换:
A率与µ变换特性曲线的折线近似法:
低通与带通信号的抽样定理:
模拟信号数字编码的基本概念:
模拟信号的数字编码主要过程:抽样、量化和编码。
抽样:把连续时间模拟信号转换成时间离散、连续幅度的抽样信号;
量化: 把时间离散、连续幅度的抽样信号转换成时间离散、幅度离散的数字信号;
编码:将量化后的信号映射成一个特定的二进制码组。
模拟信号的抽样:
抽样脉冲序列:
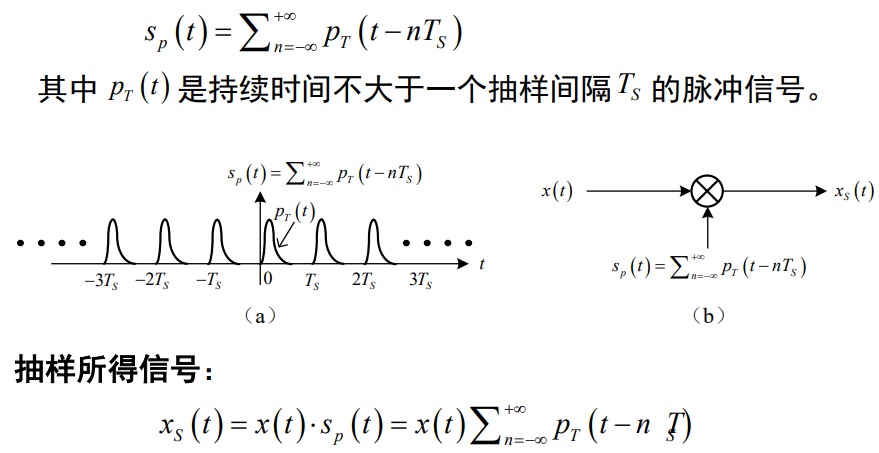
低通信号的理想抽样:

低通采样定理:
若采用间隔TS小于等于1/(2fM),则频谱不超过fM赫兹的带限信号可由其等间隔的采样值惟一确定。 采用频率fS =2fM称为奈奎斯特频率。
采样方式:
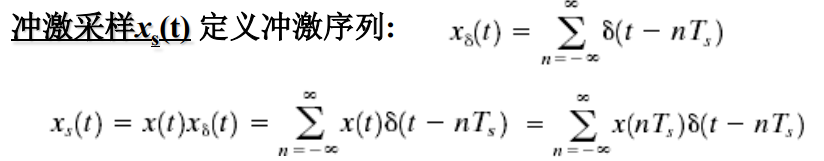
冲激采样示例:
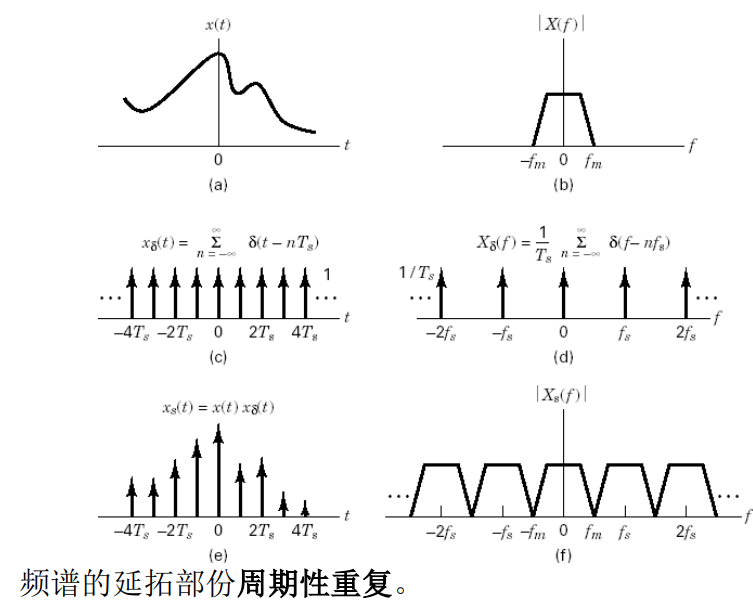
低通信号的自然抽样:

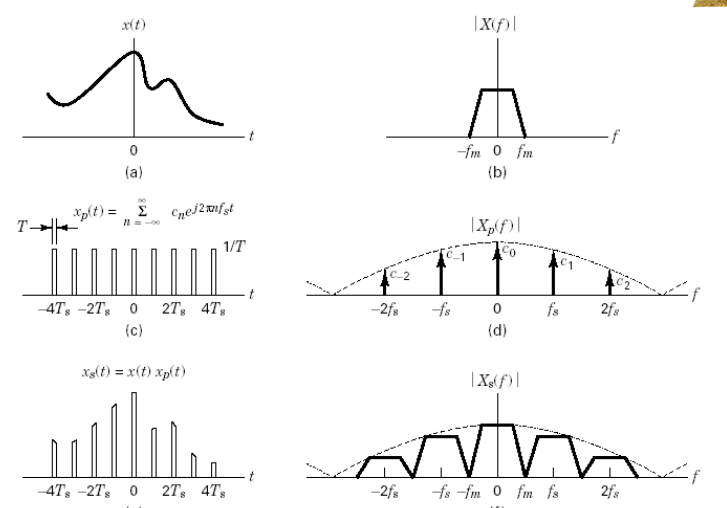
带通抽样定理:
对于带宽为W=20MHz的低通信号,所需的抽样频率
![]()
对于同样带宽的带通信号,若中心频率
![]()
若依据低通抽样定理,所需的抽样频率为
![]()
此高抽样频率的器件价格昂贵;
抽样所得的数据量巨大难以实时处理。
利用带通抽样定理,可大大降低对带通信号抽样所需的频率。

模拟信号的量化方法:
抽样信号的样值是离散的模拟信号;
未经量化的模拟信号无法通过数字通信系统传输;
模拟信号的量化:将具有无限种可能取值的模拟信号变换成只有 有限种取值的数字信号。
模拟信号的量化过程本身也是一种信号的“压缩过程”
模拟信号的量化(压缩)过程在严格意义上来说是有损的,不可逆的过程
量化的精度可以根据要求设定,使得量化对原来信号的损伤程度被控制在可以接收的范围内。
标量量化:
对抽样序列的每个样值独立地进行量化的操作称为标量量化。
标量量化方法:
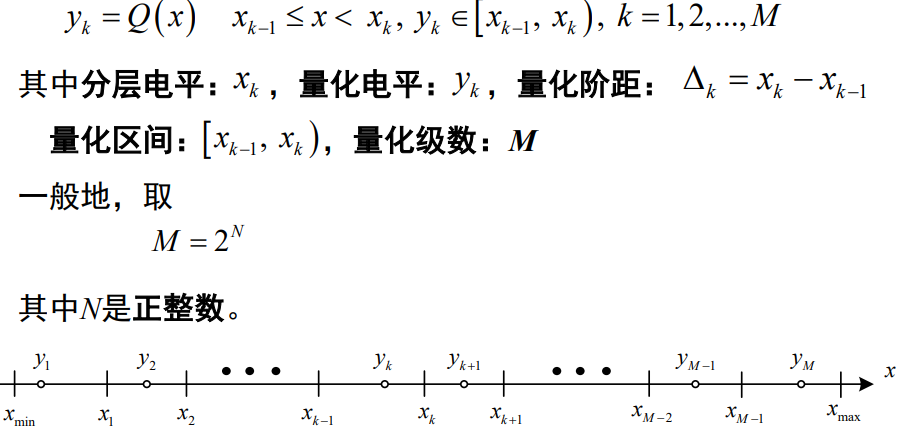
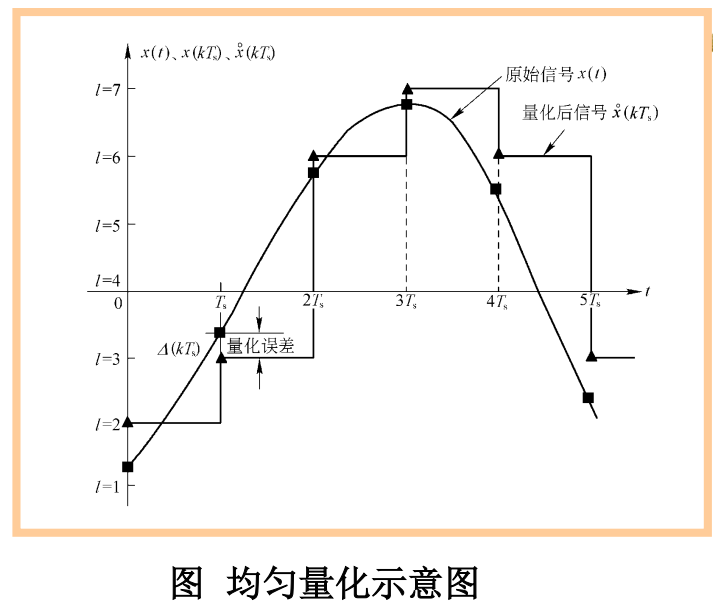
标量量化的量化方式与量化误差:
均匀量化:量化阶距为常数;均匀量化一般较为简单,易于实现
非均匀量化:量化阶距一般随输入信号的幅度而变化;非均匀量化的较为复杂,但通常有量化信噪比
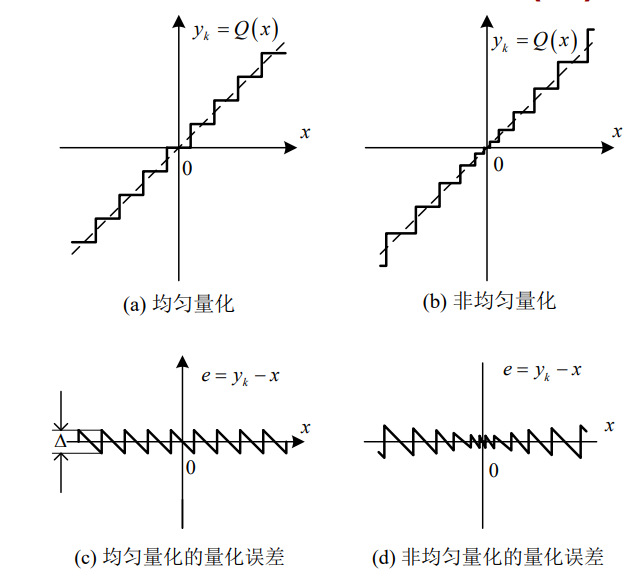
标量量化的量化噪声:
量化误差一般为随机变量,通常用量化噪声描述;
量化噪声是量化误差的归一化功率(误差电压作用在1Ω电阻上)的 统计平均值来描述
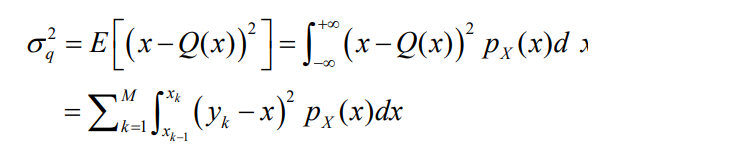
px(x)是输入信号幅度取值的概率密度函数。
常用的量化器传递函数及误差特性 e(t)= y(t) – x(t)
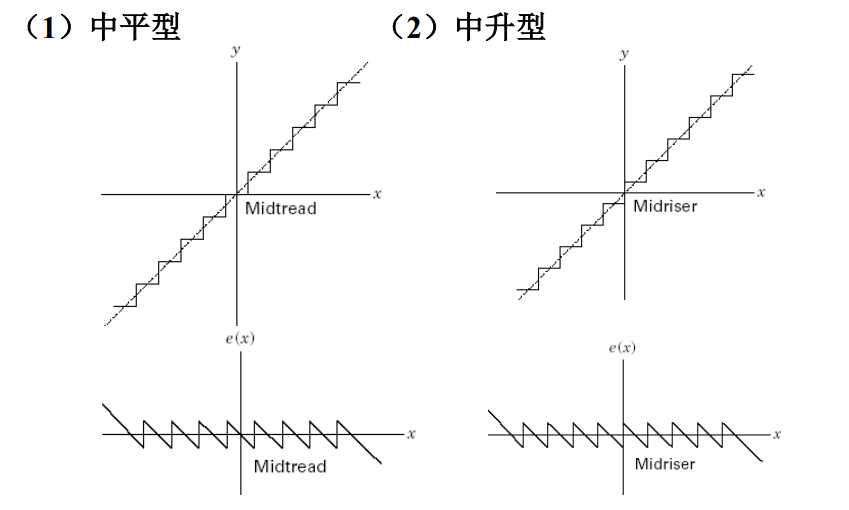
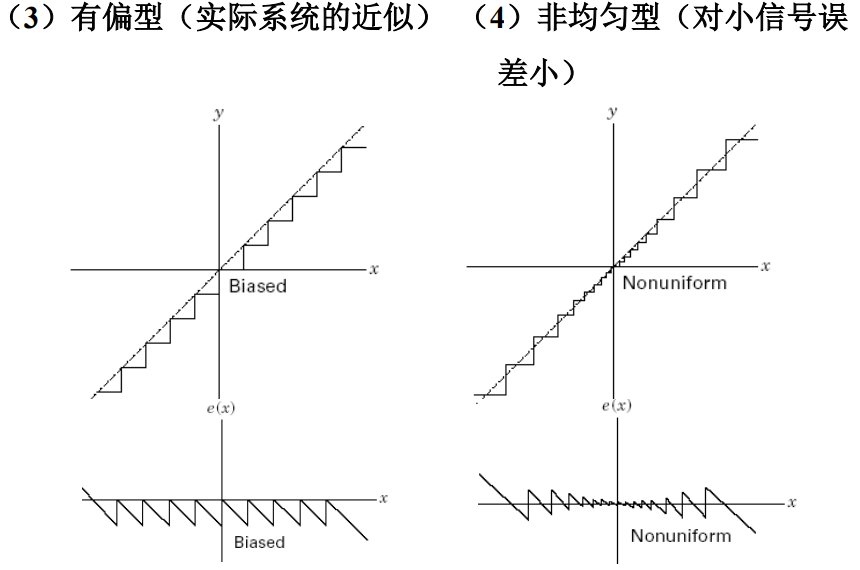
标量量化的过载噪声:

标量量化的信噪比:

矢量量化:
矢量量化:将N维空间区域分布的模拟信号矢量的抽样值映射为包含M个元素的维N矢量集中的某个元素的操作称之。
矢量量化可以表示为
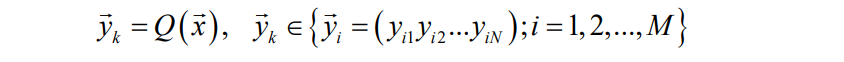
二维矢量量化的示意图
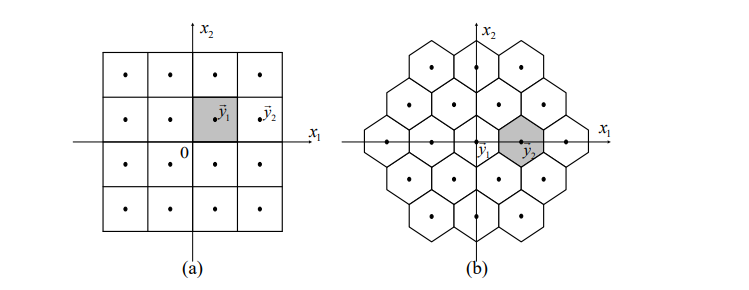

均匀量化:

量化噪声的大小仅与量化阶距有关。

重要结论:每增加一位量化精度,量化信噪比有约6dB的提升
量化噪声的简化分析计算:


非均匀量化:
对语声信号的量化,希望量化器对于小信号具有小的量化间隔,对于大信号具有大的量化间隔,使得当量化器的输入信号幅 度在相当大的动态范围变化时,量化器的输出保持近似相同的量化信噪比,从而扩大了量化器的动态范围。
研究非均匀量化的目的:寻求获得最佳量化信噪比的方法
主要研究如何改善对小信号量化时的信噪比

非均匀量化与信号恢复的工作过程:
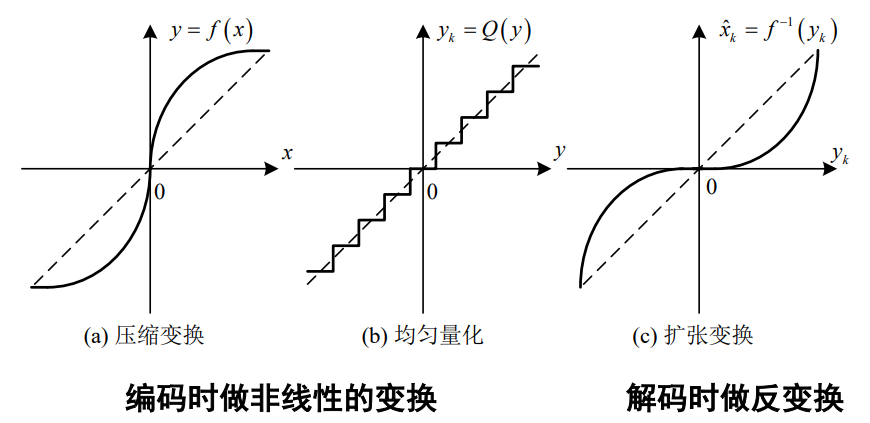
非均匀量化抑制量化噪声的原理:
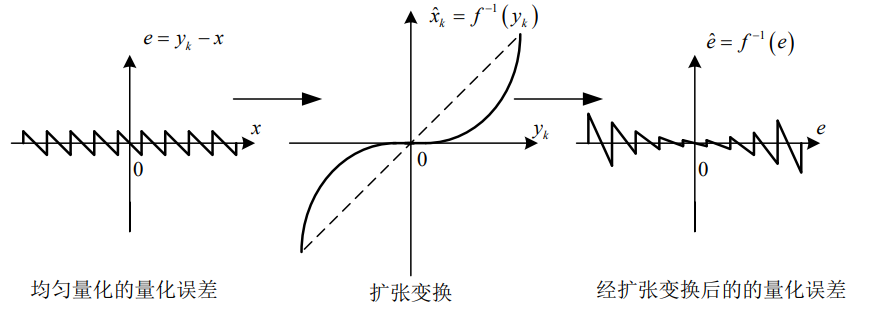
信号经历变换与反变换,信号幅度不会受到影响
量化噪声只经历反变换,在小信号区域的噪声受到抑制
对数量化:
最佳的非线性量化参数需根据输入信号调整,在实际系统中难以应用。
通信系统中最常用的语音信号的幅度取值具有拉普拉斯分布的特性,大量信号成分集中在小信号区域

为保证对语音信号有良好的量化信噪比,需要寻求一种适合语音信号的非线性量化特性
对数量化是一种量化信噪比与输入信号幅度大小无关,量化信噪比保持恒定的非线性量化方法。
相对均匀量化,对数量化方法牺牲了部分大信号时的信噪比,换取了小信号时信噪比的性能提高。
A 率对数压缩变换:
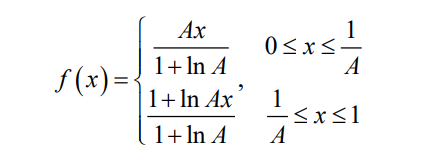
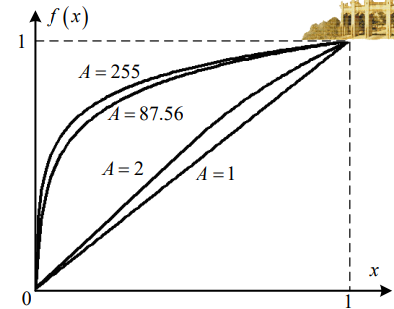
在实际标准中取 A=87.56
在小信号区域:![]()

µ率对数压缩变换:
![]()
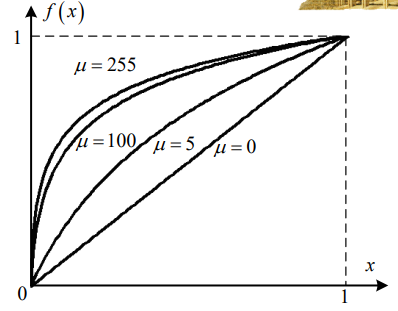
在实际标准中取 µ=255
在小信号区域:

A率与µ变换特性曲线的折线近似法:
在工程上,A率变换特性曲线通常用十三折线法近似
归一化特性近似曲线如图:

纵坐标均匀分为八段
横坐标以2倍递增扩大地 分为八段(除第2段外)
µ率变换特性曲线通常用十五折线法近似
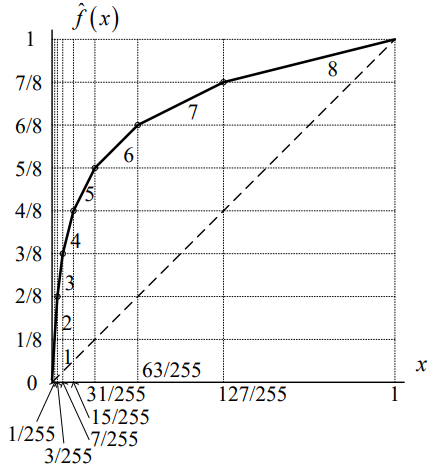
纵坐标均匀分为八段
横坐标做非均匀划分