基数排序定义

前述的各类排序方法都是建立在关键字啊比较的基础上，而分配类排序不需要比较关键字的大小，它是根据关键字中各位的值，通过对待排序记录进行若干趟分配与收集来实现排序的，是一种借助于多关键字排序的思想对单关键字排序的方法。基数排序是典型的分配类排序。

基数排序也叫桶排序或箱排序：
基本思想：分配 + 收集。
- 分配：设置若干个箱子，将关键字为 k 的记录放入第 k 个箱子；
- 收集：然后在按序号将这第 k 个箱子里的内容再拿出来链接在一起。
基数排序：数字是有范围的，均由 0 - 9 这是个数字组成，则只需要设置十个箱子，相继按照个、十、百…进行排序。

举个例子

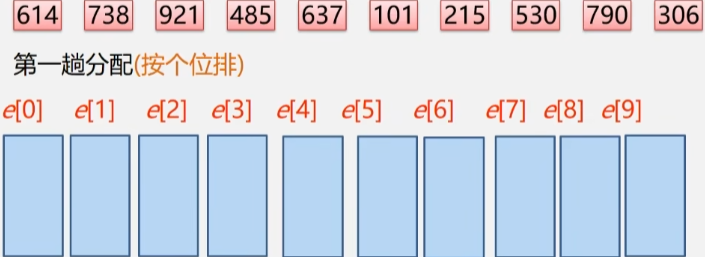
现在这样一组数据进行排序（614，738，921，485，637，101，215，530，790，306）

这一堆数据的每一位数都是由 0-9 这十个数字构成的。
准备 0-9 这十个箱子，把这些数扔到这些箱子里去。

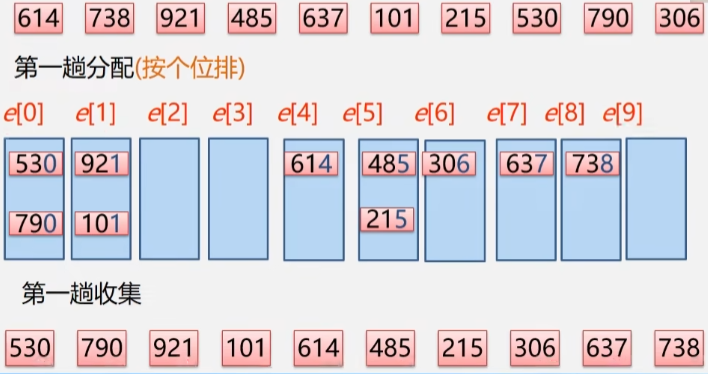
第一趟分配：按个位排，个位是多少就扔到哪个箱子里，如：614 就扔到 4 号箱子去。
- 分配完成之后，将个位数按照 0-9 的顺序将这些数据收集回来。
- 收集回来之后，这些数据的个位就有序了。

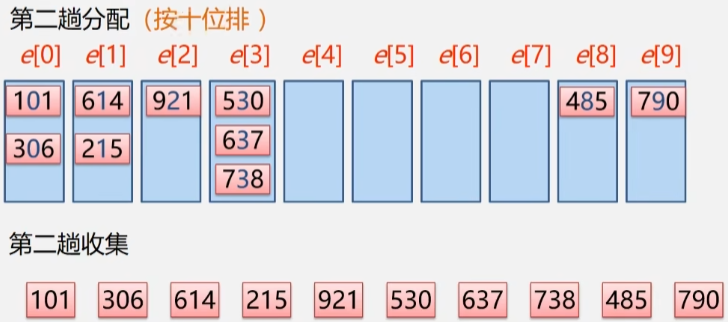
第二趟分配：按十位排
- 分配完成之后，再将十位按照从 0-9 的顺序把它们收集回来。

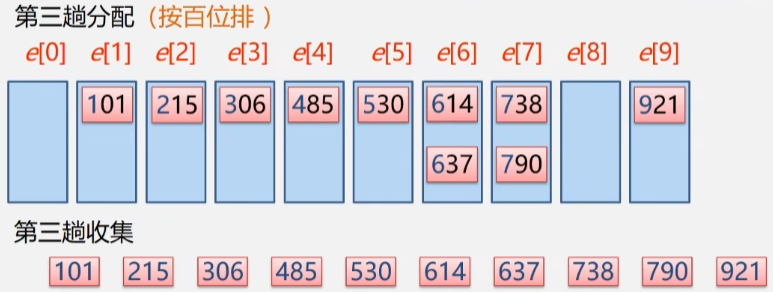
第三趟收集：按百位排
- 分配完之后再来一次收集，此时所有的数据已经有序递增了。

基数排序口诀

三分三收，个十百

基数排序算法

算法实现时采用静态链表，以便于更有效的存储和重排记录。

相关数据类型的定义：

#define MAXNUM_KEY 8 //关键字项的最大值
#define RADIX 10	//关键字基数，此时是十进制整数的基数
#define MAX_SPACE 10000

typedef struct
{
		KeyType keys[MAXNUM_KEY];//关键字
		InfoType otheritems;	//其他数据项
		int next;
}SLCell;	//静态链表的结点类型

typedef struct
{
		SLCell r[MAX_SPACE];//静态链表的可利用空间，以r[0]为头结点
		int keynum;	//记录当前的关键字个数
		int rcnum;	//静态链表的当前长度
}SLList;	//静态链表类型

typedef int ArrType[RADIX];	//数组类型

基数排序算法描述

分配算法

//静态链表L的r域中记录已按照(keys[0],...,key[i-1])有序
//本算法按照第i个关键字keys[i]建立RADIX个子表，使同一个子表中记录的keys[i]相同
//f[0...RADIX-1]和e[0...RADIX-1]分别指向各子表中第一个和最后一个元素
void Distribute(SLCell &r,int i,ArrType &f,ArrType &e)
{
		for(j = 0;j < RADIX;++j)
		{
				f[j] = 0;//将各子表初始化为空表
		}
		for(p = r[0].next;p;p = r[p].next)
		{
				j = ord(r[p].keys[i]);	//ord将记录第i个关键字映射到[0...RADIX-1]
				if(!f[j])
				{
						f[j] = p;
				}
				else
				{
						r[e[j]].next = p;
				}
				e[j] = p;	//将p所指向的结点插入第i个子表中
		}
}

收集算法

//本算法按照keys[i]自小直大将f[0...RADIX-1]所指向的各子表依次连接成一个链表
//e[0...RADIX-1]为各个子表的尾指针
void Collect(SLCell &r,int i,ArrType f,ArrType e)
{
		for(j = 0;!f[j];j = succ(j));	//找第一个非空子表，succ为求后继函数
		r[0],next = f[j];t = e[j];		//r[0].next指向第一个非空子表中的第一个结点

		while(j < RADIX)
		{
				for(j = succ(j);j < RADIX-1 && !f[j];j = succ(j));//找下一个非空子表
				if(f[j])
				{
						//链接两个非空子表
						r[t].next = f[j];
						t = e[j];
				}
		}
		r[t].next = 0;	//让t指向最后一个非空子表中的最后一个结点
}

基数排序

//对L采用静态链表表示的顺序表
//对L左基数排序，使得L成为按关键字自小到大的有序静态林彪，以L.r[0]为头结点
void RadixSort(SLList &L)
{
		for(i = 0;i < L.recnum;++i)
		{
				L.r[i].next = i+1;
		}
		L.r[L.recnum].next = 0;	//将L改造为静态链表
		for(i = 0;i < L.keynum;++i)	//按照最低位优先依次对各关键字进行分配和收集
		{
				Distribute(L.r,o.f.e);//第i趟分配
				Collect(L.r,i,f,e);//第i趟收集
		}
}

基数排序算法分析

时间复杂度

时间效率：O(k * (n + m))
- k：关键字个数（决定分配多少趟）
- n：元素个数（每一趟需要分配多少个元素）。
- m：关键字取值范围为 m 个值（桶的个数/进行收集的次数）。
分配：基数排序需要进行元素分配。
- 分配过程总共要做的次数：看关键字的个数，有个、十、百三个关键字就需要分配三次。
收集：要将每个桶内的数据收集回来。
- 收集的次数同样也是看关键字的个数。