1. 极端退化

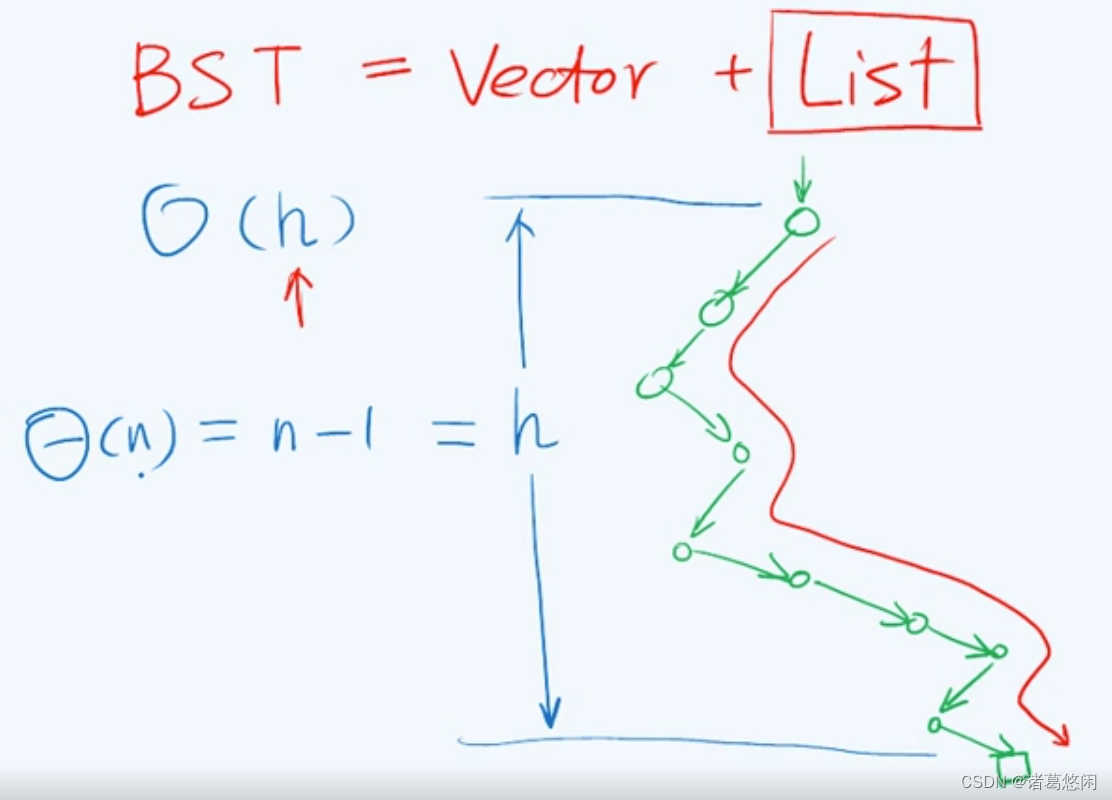
二叉搜索树为我们同时实现对数据集高效的静态操作以及动态操作打开了一扇新的大门。

正如我们所看到的，从策略上，BST可以视作是试图将此前的向量结构以及列表结构优势结合起来，然而多少令我们失望的是，我们目前所实现的BST还略微显得有些粗糙，这表现为它的时间复杂度，在最坏情况下仍未得到有效地控制。

在上一节我们讨论了BST各种接口算法的具体实现，概括而言，无论是静态的search操作，还是动态的insert或remove操作，在最坏情况下，它们所需要的时间都线性正比于树的高度O（h），然而对于BST的高度，我们至今为止还没有任何有效的控制方法。

比如作为一种极端情况，我们假设在一棵BST中，所有的节点度数都不超过1，也就是说，从整体拓扑结构而言，这棵树实际上已经退化成了一条单链，从逻辑结构看，已经完全退化地等效为一个列表。

不难看出此时整棵树的高度与整棵树中节点的个数成线性正比关系，在这种情况下，无论就平均还是最坏意义而言，静态操作以及动态操作都需要高达O（n）时间。这一结论也不足为怪，因为毕竟在此时整棵树已经退化成了一条一维列表。当然，这只是一种极端的退化情况，而若要对BST的总体性能做出一个更加客观的评价，我们或许就BST的平均性能做一个系统的分析。

2. 平均高度

以下就从两种最常见的统计口径出发，针对BST的平均高度，分别给出估算的结果，首先是所谓的随机生成统计口径。

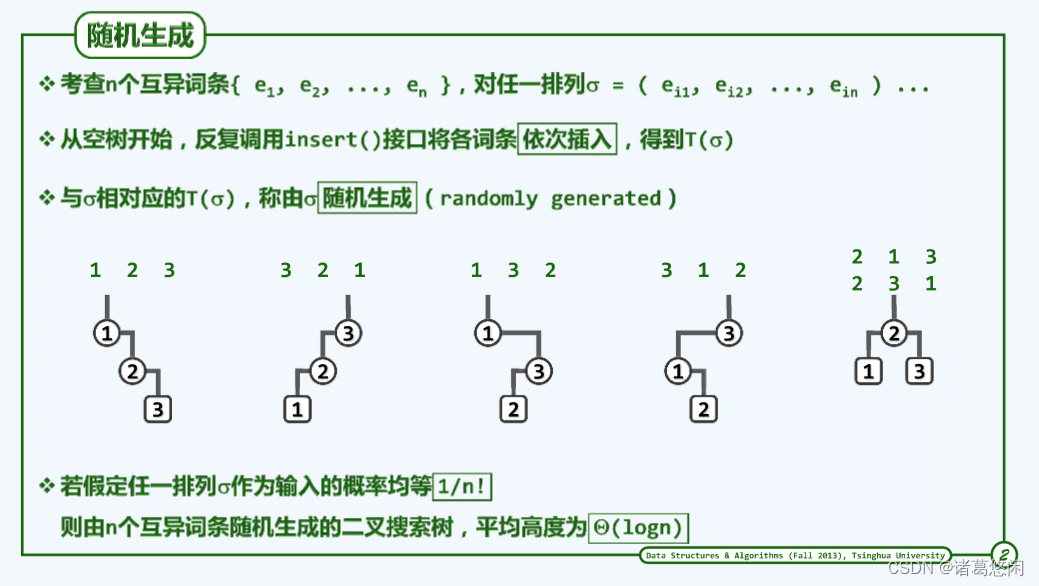
也就是说对于任何一组关键码词条，我们考察它所有可能的排列，对于其中任何一个排列，都假设按照这样的排列次序，将关键码依次插入一棵初始为空的树，比如当关键码总数为3时，依次插入 1 2 3 将会得到这样一棵BST。相应地，如果插入的次序是 3 2 1那么得到的将是这样一棵树，接下来，对于其它的排列，比如说 1 3 2 将得到这样一棵BST，以及其它的排列都会各自得到一棵BST，这样一种创建BST的方式称作随机生成。

不难发现，当关键码总数为n时，可能的生成序列也就是这n个关键码的全排列，总共有n！种。那么可以证明，如此所得到的n！棵BST平均高度为logn。

考察的第二种统计口径是所谓的随机组成。

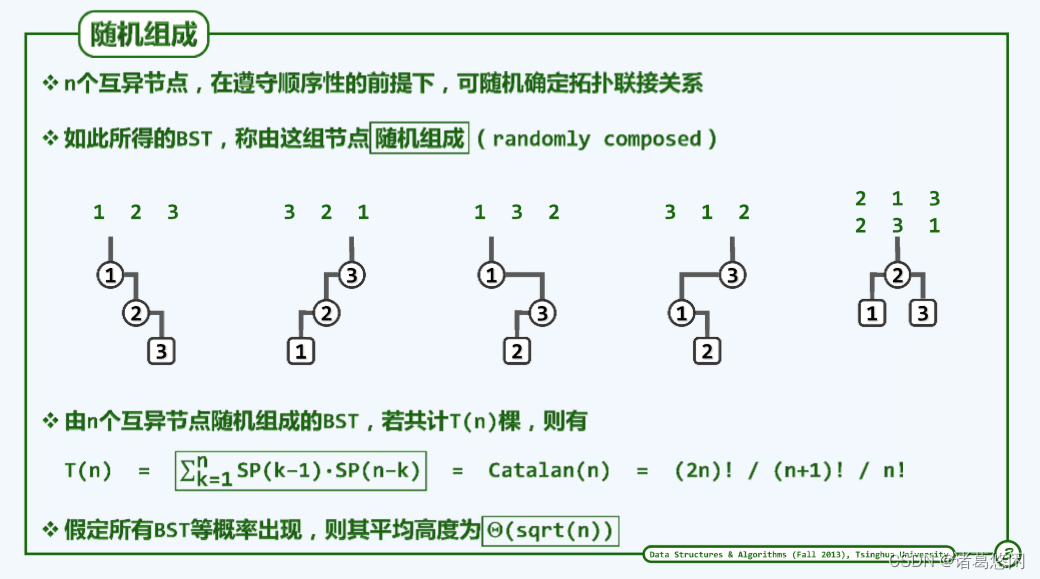
也就是说，将所有的n个关键码视作n个互异的积木，然后在符合BST顺序性要求的前提下，考察它们总共能够拼接出多少棵拓扑结构互异的BST。可以证明，如此所得BST的总数恰好为我们熟知的Catalan（n）数，而按照这一统计口径，所有BST的平均高度为O($\sqrt{n}$) 。是的，你没有听错和看错的确是$\sqrt{n}$。

你现在可能会质疑，按照我们刚才所说的随机生成统计口径，累计生成的BST应该是n的阶乘种，而且对应估算出的平均树高应该是logn。那么根据这两种口径，各自所得到的结论哪一个更为可信呢？

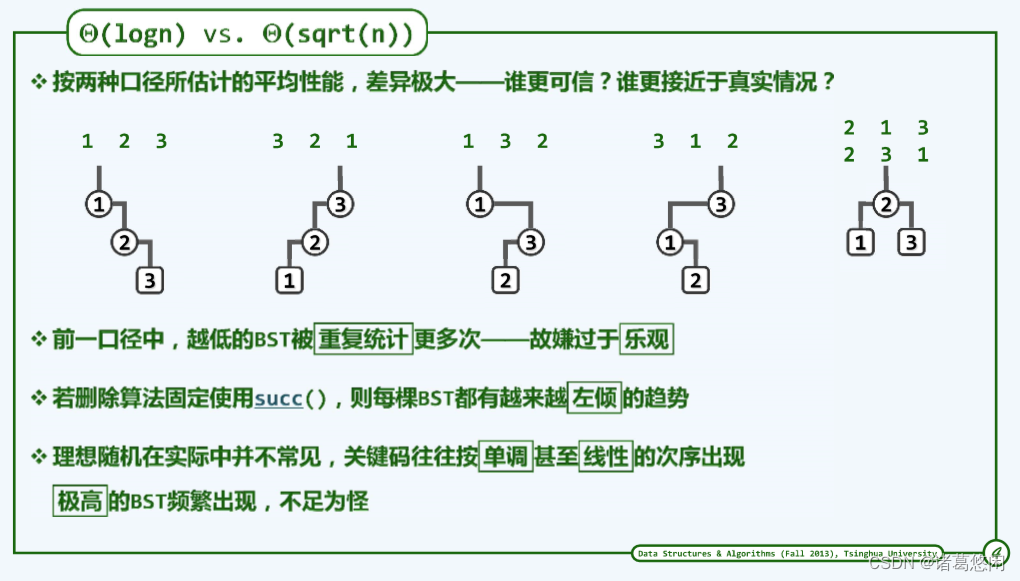
我们说后者更为可信。

其原因在于前者实际上是有所重复的，这种重复性就体现在不同的关键码序列有可能会生成同一棵BST。比如对n为3的情况而言，这样两个输入序列所生成的都是这样同一棵BST。也就是说，只要第一个插入的是居中的2，那么分列于它左右的1和3究竟是按什么次序输入是没有关系的。实际上不难理解，这个结论可以进一步推广，也就是说中位数或者接近中位数的关键码越是被更早地插入，整体而言，这棵BST的高度也相应地会更低，这就意味着在前一种统计口径中，这类高度更低的BST将会以更高的重复度参与统计以及最终的平均估算，这也是为什么按照前一统计口径所得到的估算值会相对更小。

从这一观点来看，前一统计口径可以说是过于乐观了，而后一统计口径所得到的结论将更为可信。但对于在此非常在意树高的我们来说这并不是个好消息，这意味着在天然的随机意义下，这样一个高度是不能令我们满意的。

为了进一步地降低和控制这个高度值，我们应该做点什么？而且我们很快就会看到，为此我们将不得不发现并且利用一系列的技巧。

3. 理想 + 适度

为了有效地控制树的高度，我们或许首先应该弄明白，什么样的树相对而言高度是更低的。

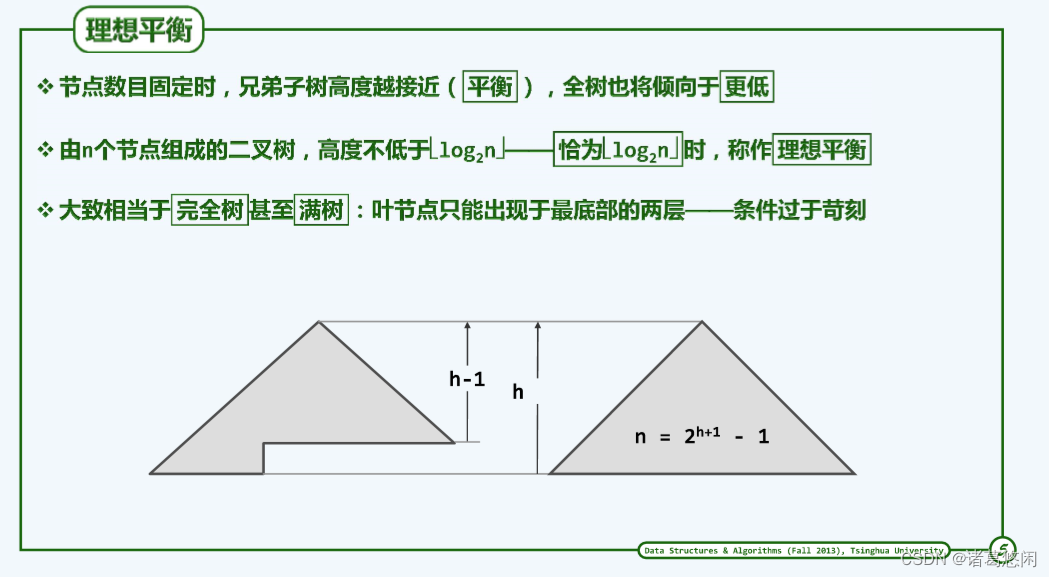
我们会发现，在节点数目相对固定时，左右兄弟子树的高度越是接近全树通常也会更加倾向于高度更低。

也就是说，全树越是接近于平衡，那么它的高度也会倾向于更低，因此我们可以通过控制全树的平衡度，以控制全树的高度。

关于树的高度，有这样一个结论：由n个节点所组成的二叉树，其高度最低不会少于|$lo{g}_{2}n$|。因此如果某棵树的高度能够达到这样一个理想的下限，我们也称之为理想平衡的。

那么哪些树能够达到这样的理想平衡状态呢？你应该会联想起我们此前所讲过的完全二叉树——条件过于苛刻。

是的，在这样的树中，叶节点只能出现在最底层以及次底层，当然，其中最好最好不过的自然是所谓的满二叉树。然而很遗憾，这样的树在实际应用中只能是可遇而不可求的，而且即便BST在某一个时刻能够达到这样高度紧凑的形式，在接下来的动态操作过程中，这样一种完美的形式也是难以持续的。因此，所谓的理想平衡在实际应用中是不具任何意义的，是的，理想平衡出现的可能性非常非常的低，而且为了维护这样的理想平衡，我们的计算成本也相应地会十分的高昂，相对而言，我们会得不偿失。

而真正可行的方法是，我们或许应该适度地放松平衡的标准，没错，适度的放松，你或许会联想起我们此前的渐进分析，没错，那正是我们的一个法宝。

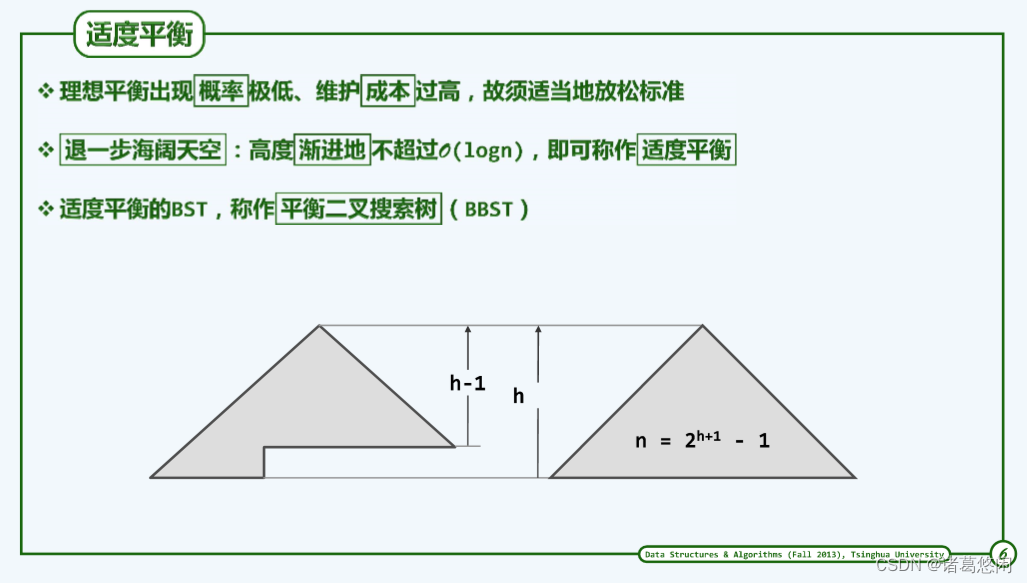
实际上只要能够保证全树的高度能够从渐进的意义而言不超过|logn|，那么也就可以称之为是平衡的了，因为这种平衡并非严格意义上的理想平衡，所以我们也不妨称之为适度平衡。这样一种适当的放松，但又不失原则的方法，也就是我们所谓的退一步海阔天空。

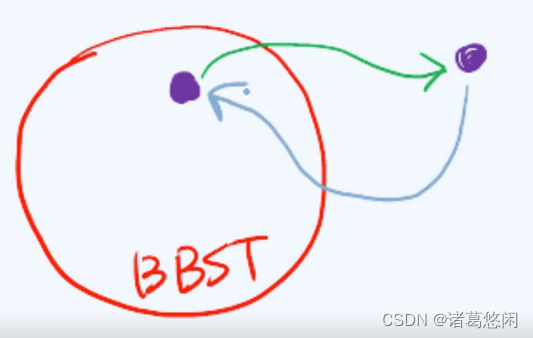
那么相应地，能够保持适度平衡的BST，也称作平衡的二叉搜索树。

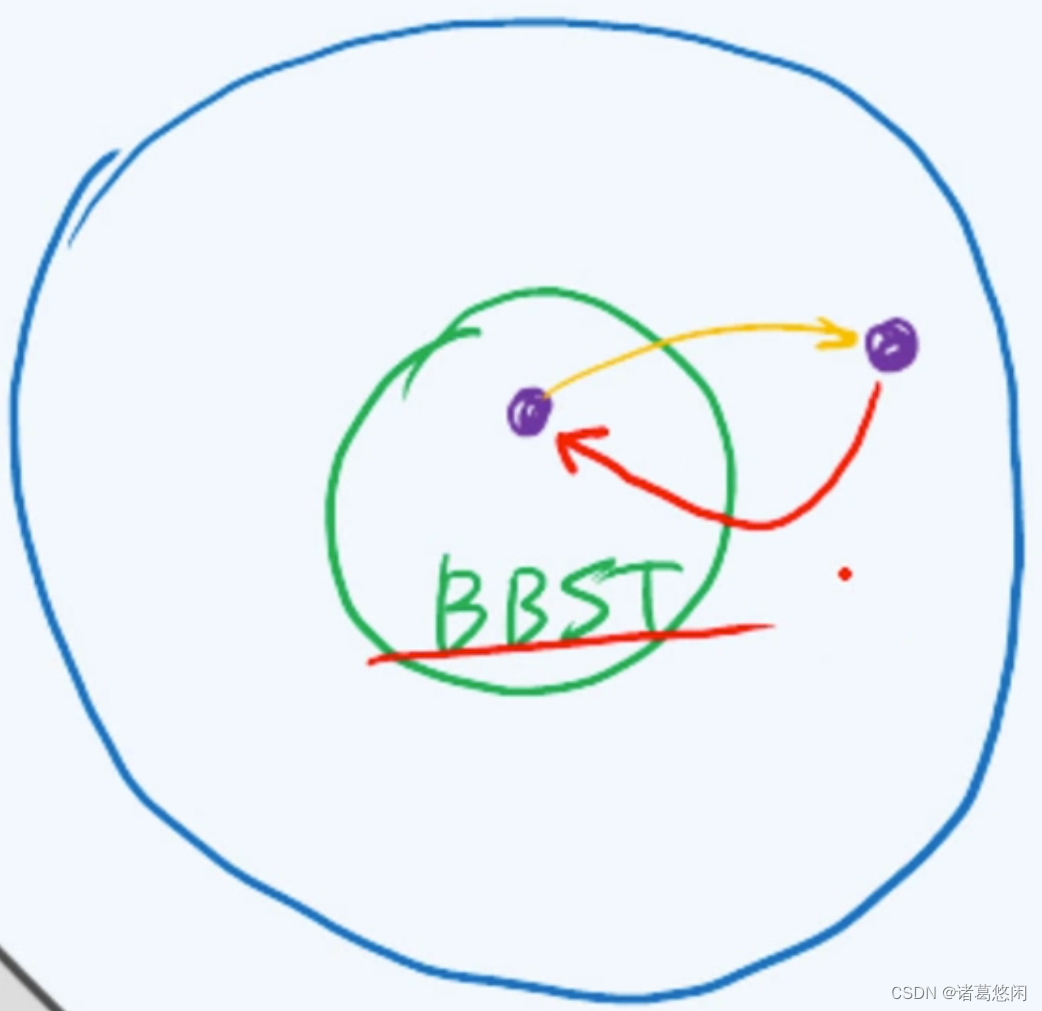
也就是说，如果将所有的BST视作一个全集，那么BBST只是其中的一个子集，对于目前而言其中任何一棵BBST，如果经过某次操作之后，它不再保持适度平衡，也就是说会游离到这个子集之外，果真如此，就需要有一整套方法，将这棵BST重新拉回到这个子集中，使它重新成为一棵BBST。

那么我们应该采用什么样的一些方法来做到这一点呢？或者先退一步，我们来考虑一下，我们可能采用哪些方法呢？
概括而言，所有的这些方法都必须是所谓的等价变换。

4. 歧义 = 等价

所谓BST，它的本质特征就是处处局部的顺序性，以及全局的单调性。

具体来说，只需考察，它的中序遍历序列是否是单调的，然而只需考察树的遍历算法，我们就不难发现，结构不尽相同的两棵BST，它们的中序遍历序列有可能是完全雷同的，这也就是我们所说的中序遍历序列的歧义性。

在某些场合中，比如中缀表达式的求值计算，这种中序遍历序列的歧义性非常令人生厌，因为我们不得不通过一些办法来明确地辨析不同操作符之间的优先级关系。

而针对BBST这样的一个问题，歧义性却变成了一个非常重要，同时也是不可或缺的一种性质。

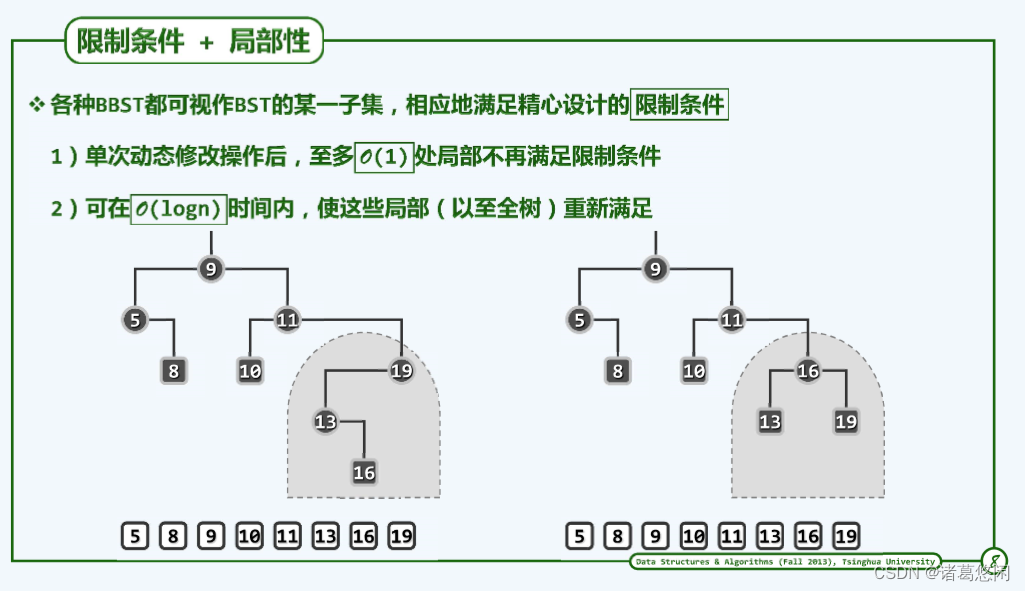
以这里所给出的两棵BST为例

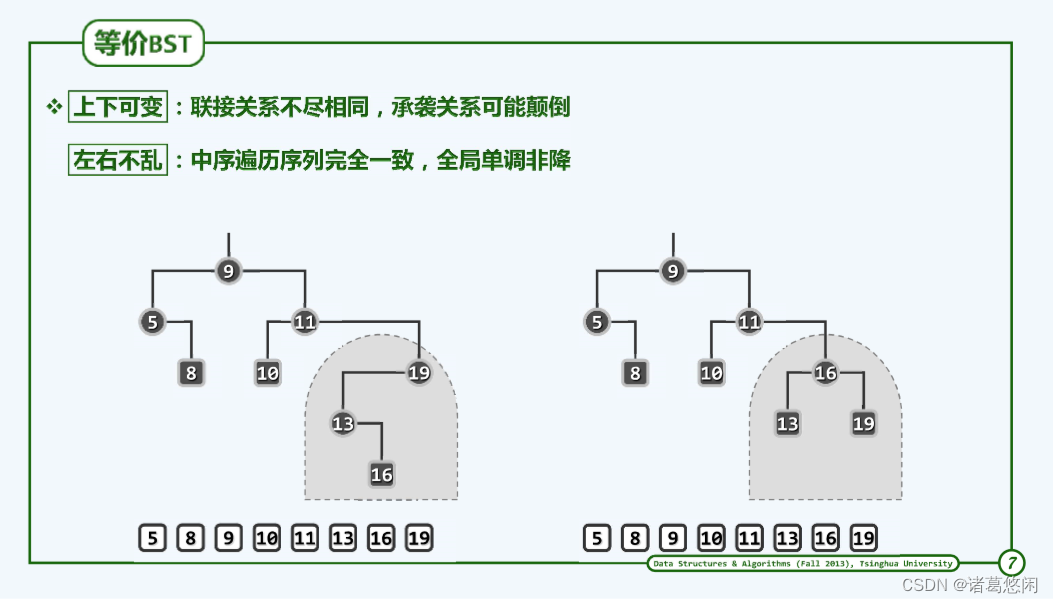
不难看出，它们都是由同一组关键码所构成的，而且它们的中序遍历序列是完全一种的。然而反过来，我们也注意到，它们的拓扑结构也不尽相同。

比如在上图局部，左侧局部子树的树根是19，而在右侧却是16，当然，还可以很容易地举出更多这样的实例。

拓扑结构不尽相同，但中序遍历序列却相同的任何一对这样的BST，也就称作相互等价的BST。

等价的BST之间，在拓扑结构上，虽然不尽相同，但也有其独特的规律，这种规律概括起来有两句话。
第一，上下可变

比如在这个例子中，19和16的祖先和后代关系就有可能在两棵树中彼此颠倒，这也可以认为等价的BST在垂直方向上有一定的自由度。

然而我们的第二条规律则是左右不能乱

这里的左右自然是指中序遍历序列，确实，相对任何一个节点，居于它右侧的节点，以及居于它左侧的节点之间不能相互混淆。

那么在这样一种上下存在一定的调整余地，但左右次序却不得颠倒的规则下，又当如何实现BST之间的等价转换呢？

5. 等价变换

实际上，任何一对等价BST之间的相互转换，都可以视作是由一系列的基本操作串接而成的，而这种基本的变换无非两类，彼此对称。其中一类如下左图

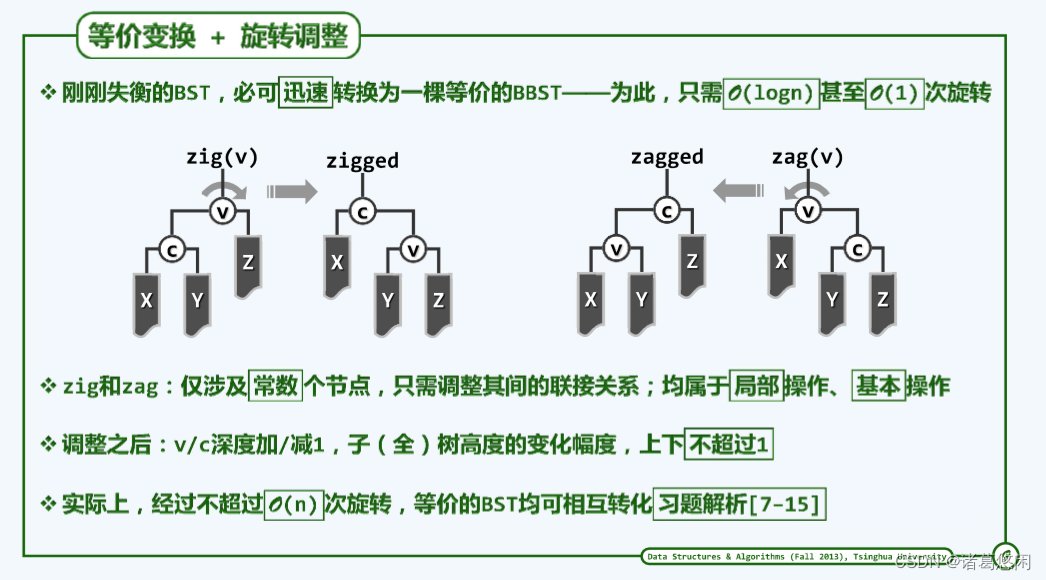
也就是说，如果节点V拥有一个左孩子C，分别有三棵子树，在此命名为 X Y Z的子树。我们只需将这局部的两个节点以及三棵子树重新调整为这样一种拓扑连接的形式（上左图）。那么无论是在此局部，还是在它们所属的那棵全树，顺序性和单调性将依然保持，也就是说，全树依然将是一棵BST。为了对此做验证，不妨来考察在此局部的中序遍历次序。无论是在变换之前，还是变换之后，在此局部，中序遍历序列的次序必然是X C Y V 以及最后的 Z 。

从效果来看，这样一个变换，可以大致理解为是在此局部围绕着节点V 做了一个顺时针的旋转，我们称这种变换为zig，那么这种旋转的中心 V 则是zig的参数。

右图是完全对称的另一种基本操作，因为它可以理解为是围绕着节点 V 做了一次逆时针的旋转操作，形象称作为zag。

在后续的章节中，我们将会看到，包括AVL树和红黑树在内的各种BBST都分别精心地定义了某种适度平衡的准则。

从而使得原本在其中的任何一棵BBST，即便在经过某次操作之后，会暂时地游离到这个边界之外，我们也总是能够通过一系列精巧地等价变换，令它重新回到这个边界以内并重新成为一棵BBST。

而在设计所有这些等价变换的组合时，我们始终不要忘了，应遵循两个重要的准则。

一个就是所谓的局部性，也就是说，我们执行的每一次等价变换，都应该局限在某一常数规模 O(1) 的局部。比如刚刚介绍的zig和zag操作而言，它们都局限在局部的V和C两个节点处，如此它们所牵涉到的节点总数既然是常数，这类操作所需要的计算时间也可以严格控制在常数的规模O(1)。第二个需要严格遵守的是，在我们将一棵刚刚失衡的BBST重新恢复为一棵BST的过程中，累计需要执行的这样的操作的次数不要过多，比如至多不要超过O（logn）次。这样就可以有效地控制整个操作序列的长度以及总体所需要的时间。

后面会看到，任何一种BBST都必须至少满足这样一个O（logn）的基本条件，但是在进一步要求上，它们各自又有所差异。

比如对于AVL树而言，它的删除操作只能刚刚达到这个及格线，而它的插入操作却可以优化到常数O(1)。而在后面将要介绍的红黑树，也就是 Red Black Tree，则可以进一步地将这两种操作的性能同时提升到最优的常数。

那么接下来的一节，就首先来看看AVL树是如何来达到这样的及格线。