核方法总结（三）———核主成分（kernel PCA）学习笔记

news2024/11/25 6:07:11

一、核主成分

1.1 和PCA的区别

PCA （主成分分析）对应一个线性高斯模型（参考书的第二章），其基本假设是数据由一个符合正态分布的隐变量通过一个线性映射得到，因此可很好描述符合高斯分布的数据。然而在很多实际应用中数据的正态性不能保证，这时用PCA建模通常会产生较大偏差。这时可以设计一个合理的非线性映射，将原始数据映射到特征空间，使数据在该空间的映射具有高斯性，在这个基础可进行有效的PCA建模。即通过核函数间接映射到特征空间再间接进行建模，所以称为核主成分分析；

1.2 推导过程

定义原始数据空间样本为 $\left \{ x_{n} \right \}$ ,非线性映射为 $\phi \left ( x \right )$ ,且在原始空间和特征空间满足如下归一化条件。

$\sum _{n}{x_{n}} = 0 \sum _{n}{\phi (x_{n})} = 0$ 1------（1）

在映射空间的协方差矩阵可写作：

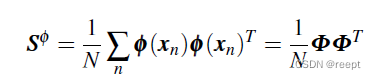1----（2）

上式中，假设 $\phi \left ( x_{n} \right )$ 有m维，则 $\phi \left ( x_{n} \right )$ $\phi \left ( x_{n} \right )^{T}$ 有m*m维。其中，在特征空间中求主成分v等价于求 $S^{\phi }$ 的特征向量：

$S^{\phi }v = \lambda v$ 1----（3）

整理以上两式可得：

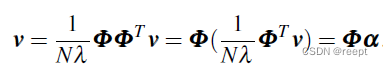1-----（4）

其中： $\alpha = \frac{1}{N\mu }\Phi ^{T}\nu$ ，是一个N维向量，其中每一维对应一个数据点与特征向量v的内积，同时，上式说明在特征空间的特征向量v由所有数据样本的向量加权平均得到，权重为 $\alpha$ ，转化为对偶问题。将 $v = \Phi \alpha$ 代回式 1 ----(4) :

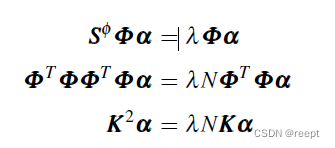1----(5)、1-----(6)、1----（7）

其中 K为gram阵，上式1—（7）右项左移，可以看出K选择合适的核函数，会使K不等于空矩阵，因而可以推出：

$K\alpha = \lambda N\alpha$ 1——（8）为1——（7）式的必要条件

考虑特征向量v应满足 $v^{T}v$ =1 ,而 v= $\Phi \alpha$ ,有：

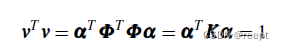1-----（9）

将1---（8）式左乘 $\alpha ^{T}$ 并代入上式，有：

$\lambda N\alpha ^{T}\alpha =1$ 1----（10）

$\alpha$ 可以通过下式求解：

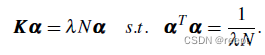1------（11）

上式求解特征向量的方法是，求解左式的特征向量，再取 $\alpha$ = $\alpha \sqrt{\frac{1}{\lambda N}}$ 就可以求得满足约束的特征向量。解出 $\alpha$ 后，即可基于1—（4）式得到在特征空间的主成分向量。和标准PCA类似，我们可以求得多个主成分，组成主成分向量集{ $v_{i}$ }。