目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
4.1灰狼优化算法原理
4.2 多目标优化问题(MOP)的帕累托最优解
4.3 基于GWO的多目标优化算法
5.完整程序
1.程序功能描述
基于GWO灰狼优化的多目标优化算法matlab仿真,目标函数为2个目标函数。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行
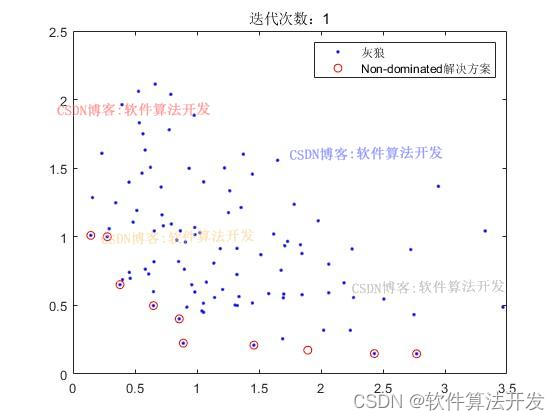
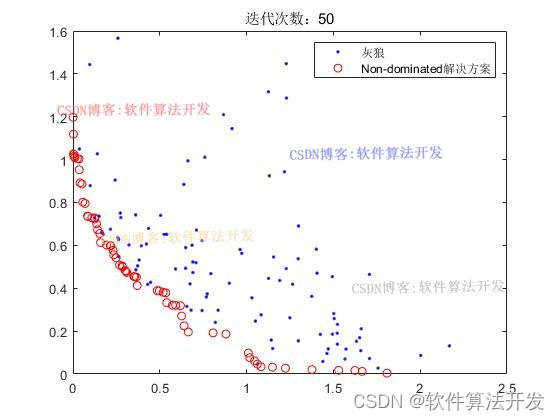
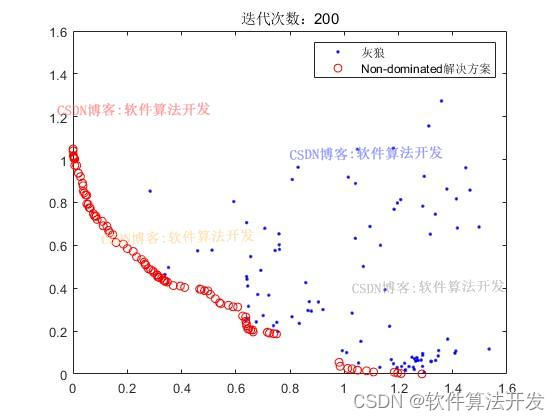
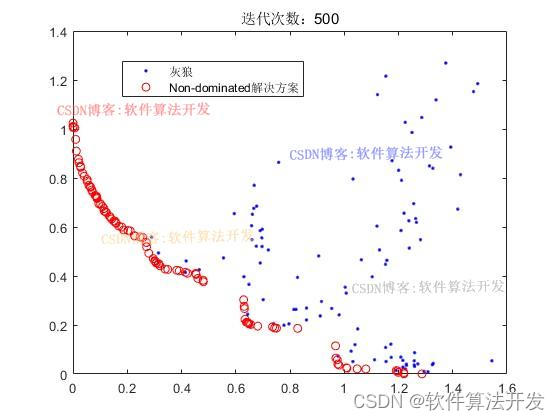
迭代1000次:

(完整程序运行后无水印)
3.核心程序
.......................................................................
% MOGWO(多目标灰狼优化)主循环
for it=1:Miters
it
% 更新支配关系并获取非支配解集
GWO0=func_domination(GWO0);
GWO0n=func_Nondomination(GWO0);
% 更新存档并执行非支配排序
GWO1=[GWO1
GWO0n];
GWO1=func_domination(GWO1);
GWO1=func_Nondomination(GWO1);
% 重新分配超立方体索引
for i=1:numel(GWO1)
[GWO1(i).GridIndex,GWO1(i).GridSubIndex]=func_index(GWO1(i),G);
end
% 控制存档大小
if numel(GWO1)>Smen
EXTRA=numel(GWO1)-Smen;
GWO1=func_Rep(GWO1,EXTRA,gamma);
ycost=func_Costs(GWO1);
G=func_Hypercubes(ycost,Ngd,alpha);
end
% 结果处理与绘图
costs=func_Costs(GWO0);
ycost=func_Costs(GWO1);
figure(1)
plot(costs(1,:),costs(2,:),'b.');
hold on
plot(ycost(1,:),ycost(2,:),'ro');
legend('灰狼','Non-dominated解决方案');
hold off
drawnow
if it==1
figure(2)
plot(costs(1,:),costs(2,:),'b.');
hold on
plot(ycost(1,:),ycost(2,:),'ro');
legend('灰狼','Non-dominated解决方案');
title(['迭代次数:',num2str(it)]);
end
if it==50
figure(3)
plot(costs(1,:),costs(2,:),'b.');
hold on
plot(ycost(1,:),ycost(2,:),'ro');
legend('灰狼','Non-dominated解决方案');
title(['迭代次数:',num2str(it)]);
end
if it==200
figure(4)
plot(costs(1,:),costs(2,:),'b.');
hold on
plot(ycost(1,:),ycost(2,:),'ro');
legend('灰狼','Non-dominated解决方案');
title(['迭代次数:',num2str(it)]);
end
if it==500
figure(5)
plot(costs(1,:),costs(2,:),'b.');
hold on
plot(ycost(1,:),ycost(2,:),'ro');
legend('灰狼','Non-dominated解决方案');
title(['迭代次数:',num2str(it)]);
end
end
644.本算法原理
灰狼优化(Grey Wolf Optimizer, GWO)是一种基于群体智能的全球优化算法,由Mirjalili等人在2014年提出,灵感来源于灰狼在自然界中的狩猎行为。该算法通过模拟灰狼的社会层级结构和狩猎策略,有效地搜索解空间,以找到问题的最优解。将GWO应用于多目标优化问题(Multi-Objective Optimization Problems, MOOPs),则形成了基于GWO的多目标优化算法,它能够处理具有多个冲突目标函数的优化问题,寻求所谓的帕累托最优解集。
4.1灰狼优化算法原理
在GWO中,算法中的每个搜索代理(解)被称作一只“狼”,它们在解空间中搜索以找到最优解。算法定义了三种角色的狼:α(领导者)、β(跟随者)和δ(猎手)。搜索过程通过模仿灰狼的领导模式、追捕猎物和群体协作行为进行。
算法步骤:
- 初始化:随机生成初始狼群,并计算每个狼的位置(解)的适应值。
- 更新α、β、δ:根据适应值确定当前群体中的领导者、跟随者和猎手。
- 更新位置:根据领导者的位置和其他狼的位置更新每只狼的位置。
- 评估并更新:计算新位置的适应值,并更新α、β、δ。
- 重复步骤2-4,直至满足停止准则(如迭代次数、适应值收敛)。
4.2 多目标优化问题(MOP)的帕累托最优解
在多目标优化中,帕累托最优解是指不存在另一个解在所有目标函数上都优于它,至少在一个目标上更好,其余目标至少一样好。寻找帕累托前沿(即所有非支配解的集合)是多目标优化的核心。
4.3 基于GWO的多目标优化算法
将GWO应用于多目标优化,关键在于如何在多目标环境下定义适应值和更新策略,以保证算法能够有效地探索和维护帕累托前沿。一种常用的方法是引入多目标适应度评价和多目标优化策略,如非支配排序和拥挤距离计算。

基于GWO的多目标优化算法通过模仿灰狼的社交行为和策略,结合多目标优化中的非支配排序和拥挤距离等策略,能够有效地搜索多目标优化问题的解空间,发现帕累托前沿解集。这种方法不仅保持了GWO的高效搜索能力,而且增加了处理多目标问题的能力,适用于解决工程、经济、环境等领域的复杂决策问题。
5.完整程序
VVV