279. 完全平方数

难度：中等
力扣地址：https://leetcode.cn/problems/perfect-squares/

没有刷过的小伙伴们请一定要先去刷一次，然后如果感兴趣的话再阅读以下内容，便于交流 ~ 多谢支持 ~

问题描述

给你一个整数 n ，返回 和 为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

• 1 <= n <= $10^4$

问题分析

首先应当明确两点：

• 这是一个 动态规划 问题；
• 这是动态规划中的 背包问题 。

如果对背包问题或者动态规划都不太了解也不碍事，那么可以先添加几个测例，并且我们做一波分析，考虑到直接阅读文字有点无聊，我做了几页PPT，请阅读以下截图。

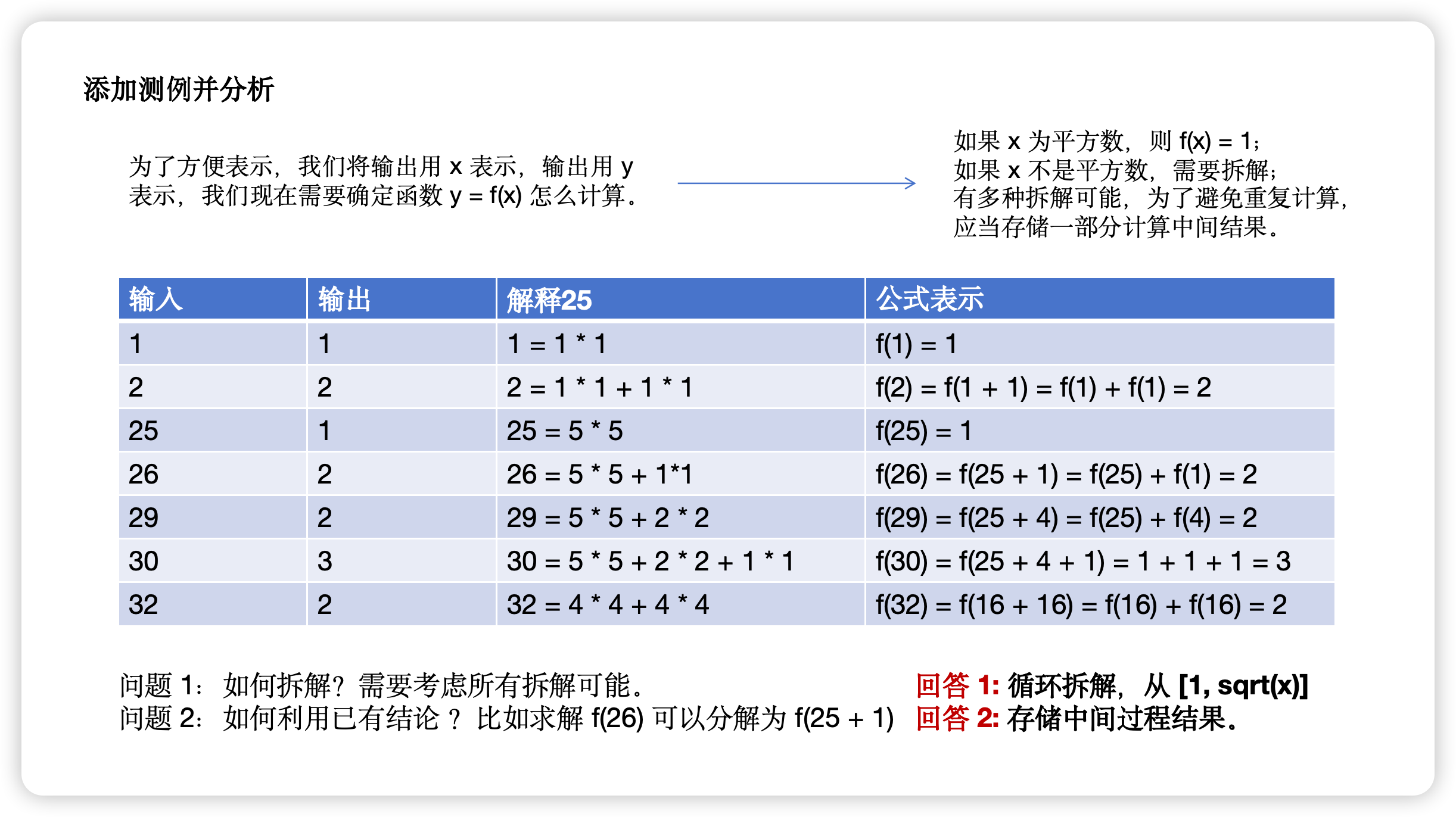
这一页 PPT 内容有点多，不过总体来说也是比较容易理解，接下来我们需要想想如何拆解。

代码编写

注释比较详细，建议考虑结合PPT的内容与注释理解每一行代码的作用。

class Solution {
public:
    int numSquares(int n) {
        // 存储所有对应的可能的结果，此处的 answers[n] 就等同于PPT中我们描述的 f(n)
        // 比如 f(25) = 1，表示 n 为 25 时，结果为 1
        // 比如 f(10) = 2，表示 n 为 10 时，结果为 2 即 10 = 3 * 3 + 1 
        int answers[n + 1];
        // answer[0] 表示，如果某个数是平方数，那么后面计算的 left 就为 0，
        // 所以对于完全平方数，answer 就应该为 answer[0] + 1 表示最少一种拆解结果
        answers[0] = 0;
        // 求解历史的结果，便于我们作差后回来找历史结果
        // 比如求解 f(26) 时，left = 26 - 1 * 1 = 25，如果我们已经计算 f(25) = 1
        // 因此 f(26) = 2
        for (int i = 1; i <= n; i++) {
            // 初始化一个超级大值，便于以后做 min 计算
            int ans = INT_MAX;
            // 拆分的结束条件，因为 left = i - pow
            // 如果 j > end，那么 i - pow 将会小于 0，这不合理
            // 因为我们希望拆解为 i = j * j + left 并且 left 一定大于等于 0
            int end = sqrt(i);
            // 尝试所有可能的拆解方式
            // 比如 f(32) = f(16) + f(16), f(32) = f(25) + f(4) + f(3)
            // 我们需要循环算所有拆解可能，并求最小的结果，记录到 ans 中 
            for (int j = 1; j <= end; j++) {
                int pow = j * j;
                int left = i - pow;
                ans = min(ans, answers[left] + 1);
            }
            // answers[i] 记录了 n 为 i 时的最小结果，也就是在所有拆解方式中，
            // 这种方式分解后的整数个数最小
            answers[i] = ans;
        }
        // 返回 f(n) 的结果
        return answers[n];
    }
};

• 时间复杂度：$O(n\sqrt{n})$
• 空间复杂度：$O(n)$

总结

这个题最重要的点应该包括：

1. 状态转移方程：
   • 如果 $x$ 不是平方数，$f(x)=\min (f(x_1)+f(x-x_1))$，即拆解为两个数的计算值，并且在所有的 $f(x_1)+f(x-x_1)$ 的结果中，找到最小的作为我们的最终结果；比如 $f(26)=f(1)+f(25)=2$
   • 如果$x$是平方数，则返回 1；比如 $f(4)=1$
2. 存储中间计算过程，比如求解 $f(26)$ 时，我们存储了 $f(25)$ 的结果。

多谢小伙伴们的支持 ~