一、问题

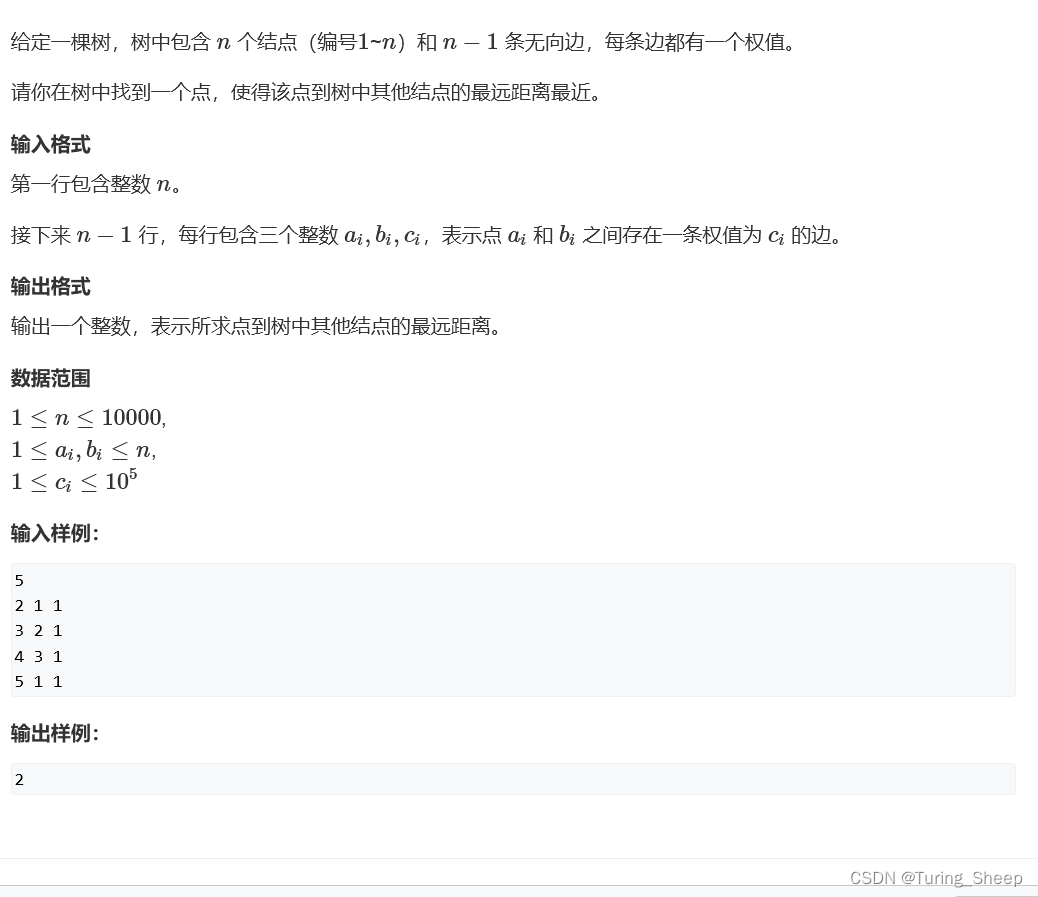
二、思路

1、暴力做法

这道题其实暴力的做法很简单，我们可以利用DFS去求出每个点到达树中其他点的最远距离。然后在这些最远距离中选出一个最大值。

暴力做法的代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+10,M = 2*N,INF=0x3f3f3f3f;
int h[N],e[M],ne[M],w[M],idx;
int ans = INF;
void add(int x,int y,int z)
{
    e[idx]=y,w[idx]=z,ne[idx]=h[x],h[x]=idx++;
}
int dfs(int u,int father)
{
    int maxv=0;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==father)continue;
        maxv=max(maxv,dfs(j,u)+w[i]);
    }
    return maxv;
}
int main()
{
    memset(h,-1,sizeof h);
    int n;
    cin>>n;
    for(int i=0;i<n-1;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c),add(b,a,c);
    }
    for(int i=1;i<=n;i++)
    {
        ans=min(ans,dfs(i,-1));
    }
    cout<<ans<<endl;

    return 0;
}

那么我们分析一下这个做法是否可行。

我们想要知道一个树中的一个点到达树中其他点的最远距离的话，就需要去遍历树中的所有点，这个过程的时间复杂度就是$O(n)$，而我们需要对n个点都进行同样的操作，这样才能在这些最大的距离中挑出一个最小的。那么总的时间复杂度就是$O(n^2)$。那么我们的运行次数最多就是$10^4\ast 10^4=10^8$这样做的效率就非常低了，很容易超时。

现实的确如此：

2、树形DP+换根DP

（1）思路分析

这道题在进行DP的分析之前需要大家会另外一道题，AcWing 1072. 树的最长路径（DFS与树形DP）

这道题就是在那道题的基础上做出的变形。

这道题的关键问题是如何高效地解决当前点到其他点的最远距离，我们可以将这些距离分个类，总共分为两类，一类是该节点沿着子树出发，到子树中某个节点的距离，另一类是从该节点的父节点出发，通过父节点到那些非该点的子树的点的距离。

即一个是向下出发的最大值，一个是向上出发最大值。这两个最大值之间的最大值就是我们想要求的。

可以用下面的图表示：

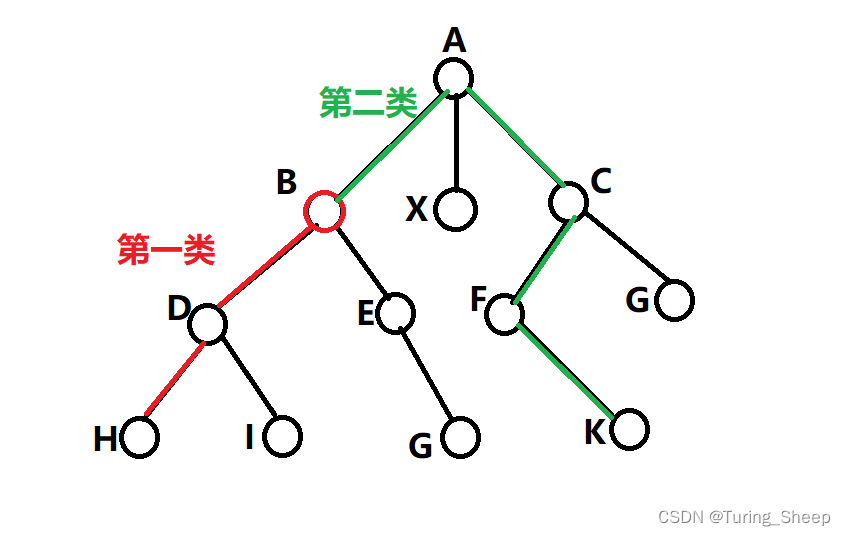
通过子树的最大值的求法，即向下出发的最大值就是我们刚才说的那道题中的求法，只需要将那道题中的dfs函数原封不动的移动过来即可。AcWing 1072. 树的最长路径（DFS与树形DP）

在这里主要讲解的是如何求向上出发的最大值。

在向下出发的最大值中，可能有很多情况，因为一个点可能会连接很多的子节点，但是向上出发的就不一样了。因为这是个树，而树中的子节点的父节点只有一个。因此，我们只需要考虑一种从父节点出发的情况。

我们以图中的B点为例子：

B点的父节点是A，那么B点的第二类距离可以描述为，B点到父节点A的距离加上A点到非B点的最大值。

那么对于A点而言，我们知道A点的距离有：A点向下出发的最大值和次大值，以及A点向上出发的最大值。

因此，我们需要在这三个值之间求出一个最大值再加上我们B到A的距离，就是B点向上出发的最大值。

这么想对吗？

我们考虑下面一种情况：

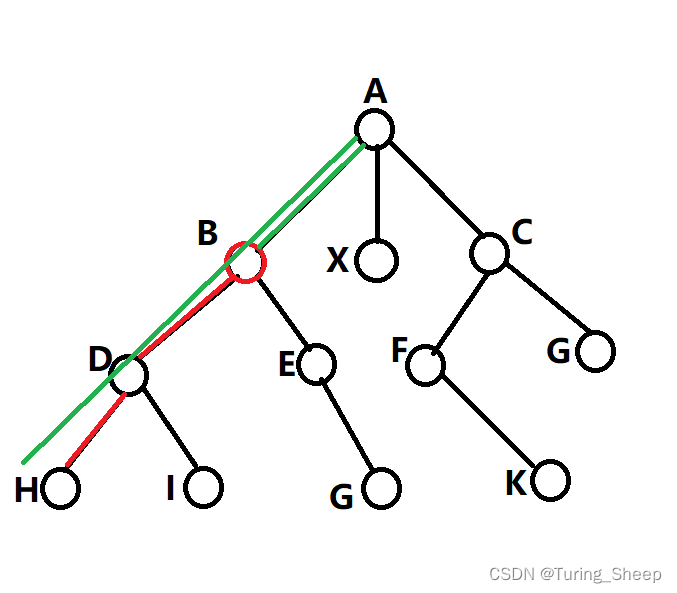
因为B点是A点的子节点，所以A点向下出发的距离中的最大值有可能是经过B点的，比如图中的绿线表示的情况，此时如果按照我们刚才的理解，最后的比较结果就有可能出现，A到B的距离加上A的向下出发的距离中的最大值，此时这个方式所描述的路线经过了2次B点。

这种情况是不合法的，也就是说此时我们只能在求解B点向上的最大值的时候，只能比较A点向下的次大值和A点向上的最大值。

相反如果A点向下的最大值不经过B点，那么我们只需要在A点向上的最大值中和A点向下的最大值中求出一个最大值。

说到这里，上面所说的两种情况就是我们接下来求解的思路了。为了方便两种情况之间的判断，我们还需要再开辟两个数组去记录向下出发距离中次大值和最大值是从哪个子节点转移过来的。

那么我们用$f[1][u]$和$f[2][u]$分别表示向下出发的次大值和最大值。

然后利用$g[u]$表示向上出发的最大值。

$s[1][u]$和$s[2][u]$分别表示u点向下出发的最大值经过子节点和向下出发的次大值经过的子节点。

状态转移方程就是我们上面描述的过程。

那么我们求向下的最大值是利用子节点更新父节点，而求向上的最大值是利用父节点更新子节点，前者就是普通的树形DP而后者则是树形DP的变形，叫做换根DP。

换根DP的代码的区别又在哪里呢？

我们看下面的讲解。

（2）普通树形DP与换根DP的区别

我们发现求第一类的时候，我们是用子节点去更新父节点，但是求第二类的距离的时候我们是用父节点更新子节点的。

那么这种利用父节点更新子节点的方式叫做：换根DP

那么普通的树形DP和换根DP是怎么体现的呢？

其实这就是一个先后更新的问题：

我们直接看下面的结果：

普通的树形DP

void dfs(int u,int father)
{
		for(遍历子节点)
		{
			dfs(子节点，u);
			dp[u]=xxxx;//更新dp数组
		}	
}

换根DP

void dfs(int u,int father)
{
		for(遍历子节点)
		{
			dp[u]=xxxx;//更新dp数组
			dfs(子节点，u);
		}	
}

这两个DP的唯一区别就是DFS和DP数组更新的顺序不同。

很好理解，换根DP是先更新父节点，再利用父节点去更新子节点，因此需要先执行dp数组更新的代码。普通的树形DP相反。

三、代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+10, M = 2 * N;
const int INF = 0x3f3f3f3f;
int h[N], e[M], ne[M], w[M], idx;
int f[4][N];
int s[2][N];
int g[N];

void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c;
    h[a] = idx++;
}

void dfs_d(int u, int father)
{
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(j == father)continue;
        dfs_d(j, u);
        if(f[1][j] + w[i] >= f[1][u])
        {
            f[2][u] = f[1][u];
            s[2][u] = s[1][u];
            f[1][u] = f[1][j] + w[i];
            s[1][u] = j;
        }
        else if(f[1][j] + w[i] >= f[2][u])
        {
            f[2][u] = f[1][j] + w[i];
            s[2][u] = j;
        }
    }
    return;
}

void dfs_u(int u ,int father)
{
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(j == father)continue;
        if(j == s[1][u])
            g[j] = max(f[2][u], g[u]) + w[i];
        else
            g[j] = max(f[1][u], g[u]) + w[i];
        dfs_u(j,u);
    }
}

int main()
{
    memset(h, -1, sizeof h);
    int n;
    cin>>n;
    for(int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    dfs_d(1, -1);
    dfs_u(1, -1);
    int minv = INF;
    for(int i = 1; i <= n; i ++ )
    {
        minv = min(minv, max(g[i], f[1][i]));
    }
    cout<< minv << endl;
    return 0;
}