C/C++ 高精度（加减乘除）算法压位优化

news2025/11/4 19:28:50

文章目录

  • 前言
  • 一、基本原理
    • 1、存储方式
    • 2、计算方式
  • 二、完整代码
  • 三、性能对比
  • 总结
  • 附录
    • 1、性能测试代码

前言

由于上一章《C/C++ 高精度（加减乘除）算法简单实现》实现了基本的高精度计算，数组的每个元素存储一位10进制的数字。这样的存储方式并不是最优的，32位的整型其实至少可以存储9位高精度数字，数组元素存储更多的位数就是压位优化。本文将展示压位优化的原理以及压9位的实现和性能对比。

一、基本原理

1、存储方式

压位优化就是将原本存储一位的数组元素变成存储多位，这样就可以提升运算效率，通常最高能存储9位，如下图示例为存储4位。
在这里插入图片描述

2、计算方式

采用模拟立竖式计算，比如加法的计算流程，如下图所示，20481024+80001000=100482024：

在这里插入图片描述

二、完整代码

因为接口以及使用方法与上一章《C/C++ 高精度（加减乘除）算法简单实现》是完全一致的，所以这里直接展示完整代码，省略使用示例。下面代码为压9位实现。

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<stdint.h>
/// <summary>
/// 通过字符串初始化
/// </summary>
/// <param name="a">[in]高精度数组</param>
/// <param name="value">[in]字符串首地址</param>
static void loadStr(int* a, const char* value) {
	int len = strlen(value);
	int left = len % 9;
	char s[8], * p = (char*)value + left;
	a[0] = ceil(len / 9.0);
	len = len / 9.0;
	for (int i = 1; i <= len; i++)
		sscanf(p + (len - i ) * 9, "%09d", &a[i]);
	if (left){
		sprintf(s, "%%0%dd", left);
		sscanf(value, s, &a[a[0]]);
	}
}
/// <summary>
/// 输出到字符串，
/// </summary>
/// <param name="a">[in]高精度数组</param>
/// <param name="str">[out]字符串，由外部停供缓冲区，需要保证长度足够</param>
static void toStr(int* a, char* str) {
	if (!a[0]) {
		sprintf(str, "0");
		return;
	}
	sprintf(str, "%d", a[a[0]]);
	str += strlen(str);
	for (int i = a[0]-1; i > 0; i--)
		sprintf(str +( a[0] -i-1)*9, "%09d", a[i]);
	str[(a[0]-1)*9] = '\0';
}
/// <summary>
/// 通过无符号整型初始化
/// </summary>
/// <param name="a">[in]高精度数组</param>
/// <param name="value">[in]整型值</param>
static void loadInt(int* a, uint64_t value) {
	a[0] = 0;
	while (value)a[++a[0]] = value % 1000000000, value /= 1000000000;
}

/// <summary>
/// 比较两个高精度数的大小
/// </summary>
/// <param name="a">[in]第一个数</param>
/// <param name="b">[in]第二个数</param>
/// <returns>1是a>b,0是a==b,-1是a<b</returns>
static int compare(int* a, int* b) {
	if (a[0] > b[0])return 1;
	if (a[0] < b[0])return -1;
	for (int i = a[0]; i > 0; i--)
		if (a[i] > b[i])return 1;
		else if (a[i] < b[i])return -1;
	return 0;
}
/// <summary>
/// 复制
/// </summary>
/// <param name="a">[in]源</param>
/// <param name="b">[in]目标</param>
static void copy(int* a, int* b) {
	memcpy(b, a, (a[0] + 1) * sizeof(int));
}
/// <summary>
/// 打印输出结果
/// </summary>
static void print(int* a) {
	int i = a[0];
	printf("%d", a[i--]);
	for (; i > 0; i--)printf("%09d", a[i]);
}

/// <summary>
/// 加
/// </summary>
/// <param name="a">[in]被加数</param>
/// <param name="b">[in]加数</param>
/// <param name="c">[out]结果</param>
static	void plus(int* a, int* b, int* c) {
	int* p;
	if (a[0] < b[0])p = a, a = b, b = p;//确保a长度最大	
	int i = 1, alen = a[0], blen = b[0];
	c[0] = c[alen + 1] = 0;
	if (a != c)memcpy(c + blen + 1, a + blen + 1, (alen - blen) * sizeof(int));//a多出的部分直接拷贝到结果
	for (; i <= blen; i++) {
		c[i] = a[i] + b[i];
		if (c[i - 1] >= 1000000000)c[i - 1] -= 1000000000, c[i]++;//判断上一位是否进位	
	}
	i--;
	while (c[i++] >= 1000000000)c[i - 1] -= 1000000000, c[i]++;//继续判断进位
	c[0] = c[alen + 1] ? alen + 1 : alen;//记录长度
}
/// <summary>
/// 加等于
///结果会保存在a中
/// </summary>
/// <param name="a">[in]被加数</param>
/// <param name="b">[in]加数</param>
static	void plusq(int* a, int* b) {
	plus(a, b, a);
}

/// <summary>
/// 减
/// </summary>
/// <param name="a">[in]被减数,被减数必须大于等于减数</param>
/// <param name="b">[in]减数</param>
/// <param name="c">[out]结果</param>
static	void sub(int* a, int* b, int* c) {
	int i = 1, alen = a[0];
	if (a != c)memcpy(c + b[0] + 1, a + b[0] + 1, (a[0] - b[0]) * sizeof(int));//a多出的部分直接拷贝到结果
	c[0] = 1;
	for (; i <= b[0]; i++) {
		c[i] = a[i] - b[i];
		if (c[i - 1] < 0)c[i - 1] += 1000000000, c[i] --;//判断上一位是否补位		
	}
	i--;
	while (c[i++] < 0)c[i - 1] += 1000000000, c[i]--;//继续判断补位	
	while (!c[alen--]); c[0] = alen + 1;//记录长度
}
/// <summary>
/// 减法等于
///结果会保存在a中
/// </summary>
/// <param name="a">[in]被减数，被减数必须大于等于减数</param>
/// <param name="b">[in]减数</param>
static	void subq(int* a, int* b) {
	sub(a, b, a);
}

/// <summary>
/// 乘
/// </summary>
/// <param name="a">[in]被乘数</param>
/// <param name="b">[in]乘数</param>
/// <param name="c">[out]结果，数组长度必须大于等于aLen+bLen+1</param>
static	void mul(int* a, int* b, int c[]) {
	int len = a[0] + b[0], d = 0;
	memset(c, 0, sizeof(int) * (len + 1));
	b[b[0] + 1] = 0; c[0] = 1;//防止越界
	for (int i = 1; i <= a[0]; i++)
		for (int j = 1; j <= b[0] + 1; j++){
			int64_t t = (int64_t)a[i] * b[j] + c[j + i - 1] + d;
			c[j + i - 1] = t % 1000000000;
			d = t / 1000000000;
		}
	while (!c[len])len--; c[0] = len;
}
/// <summary>
/// 乘等于
/// 累乘,结果存放于a
/// </summary>
/// <param name="a">[in]被乘数，数组长度必须大于等于2aLen+bLen+1</param>
/// <param name="b">[in]乘数</param>
static	void mulq(int* a, int* b) {
	int* c = a + a[0] + b[0] + 1;
	memcpy(c, a, (a[0] + 1) * sizeof(int));
	mul(c, b, a);
}

/// <summary>
/// 除法
/// 依赖减法subq
/// </summary>
/// <param name="a">[in]被除数,被除数必须大于除数</param>
/// <param name="b">[in]除数</param>
/// <param name="c">[out]商，数组长度大于等于3aLen-bLen+1</param>
/// <param name="mod">[out]余数，可以为NULL，数组长度大于等于aLen</param>>
static void div(int* a, int* b, int* c, int* mod) {
	int len = a[0] - b[0] + 1, times, hTimes[32], * temp = c + a[0] + 1;
	if (!mod)mod = temp + 2*(a[0] + 1)+1;//缓冲区
	memcpy(mod, a, (a[0] + 1) * sizeof(int));
	memset(c, 0, sizeof(int) * (len + 1));
	memset(temp, 0, sizeof(int) * len);
	c[0] = 1;//防止while越界
	for (int i = len; i > 0; i--) {
		memcpy(temp + i, b + 1, sizeof(int) * b[0]);//升阶	
		temp[0] = b[0] + i - 1;
		while (compare(mod, temp) != -1) {
			if (times = (mod[mod[0]] * ((mod[0] - temp[0]) ? 1000000000ll : 1)) / (temp[temp[0]] + (temp[0] == 1 ? 0 : 1)))//升倍数
			{
				loadInt(hTimes,times);
				mulq(temp, hTimes);
			}
			else times = 1;
			while (compare(mod, temp) != -1)subq(mod, temp), c[i] += times;	//减法
			memcpy(temp + i, b + 1, sizeof(int) * b[0]);//还原	
			temp[0] = b[0] + i - 1;
		}
	}
	while (!c[len])len--; c[0] = len;
}
/// <summary>
/// 除等于
/// 商保存在a
/// 依赖div
/// </summary>
/// <param name="a">[in]被除数,被除数必须大于除数</param>
/// <param name="b">[in]除数</param>
/// <param name="mod">[out]余数，可以为NULL，数组长度大于等于aLen</param>>
static void divq(int* a, int* b, int* mod) {
	div(a, b, a, mod);
}

三、性能对比

测试平台：Windows 11
测试设备：i7 8750h
测试方式：测试5次取均值
表1、测试用例

测试用例描述
1整型范围数字计算500000次
2长数字与整型范围数字计算500000次
3长数字与长数字计算500000次

基于上述用例编写程序进行测试，测试结果如下表
表2、测试结果

计算测试用例1位实现（上一章）耗时9位优化（本章）耗时
加法测试用例10.003926s0.002620s
加法测试用例20.026735s0.005711s
加法测试用例30.029378s0.005384s
累加测试用例10.003255s0.002536s
累加测试用例20.017843s0.002592s
累加测试用例30.034025s0.006474s
减法测试用例10.004237s0.002078s
减法测试用例20.024775s0.004939s
减法测试用例30.027634s0.004929s
累减测试用例10.004272s0.002034s
累减测试用例20.0054070.001942s
累减测试用例30.019363s0.004282s
乘法测试用例10.043608s0.004751s
乘法测试用例20.479071s0.028358s
乘法测试用例33.375447s0.064259s
累乘测试用例1 只计算1000次0.001237s0.000137s
累乘测试用例2 只计算1000次0.001577s0.000187s
累乘测试用例3 只计算1000次5.792887s0.081988s
除法测试用例10.025391s0.024763s
除法测试用例25.292809s0.516090s
除法测试用例30.395773s0.073812s
累除测试用例1 只计算1000次0.059054s0.035722s
累除测试用例2 只计算1000次0.103727s0.060936s
累除测试用例3 只计算500次89.748837s25.126072s

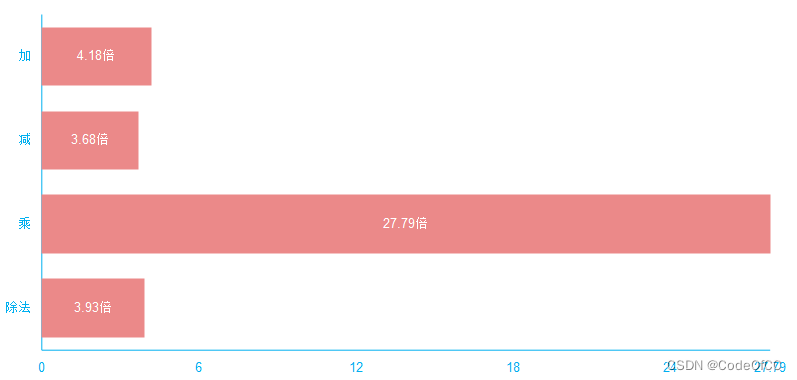
将上表数据进行分类相同类型取均值计算出提升速度如下图所示，仅作参考。

图1、速度提升
在这里插入图片描述

总结

以上就是今天要讲的内容，压位优化性能提升是比较显著的，而且实现也很容易，大部分逻辑是一致的只是底数变大了而已。从性能测试结果来看所有计算至少由4倍的提升，乘法性能提升较大有可能是测试方法不严重，这个待以后验证。总的来说，对高精度运算进行压位优化还是很有必要的，尤其是对时间和空间有要求的场景还是比较适用的。

附录

1、性能测试代码

#include<Windows.h>
#include <iostream>
static int a[819200];
static int b[819200];
static int c[819200];
static int mod[819200];
static char str[81920];
/// <summary>
/// 返回当前时间
/// </summary>
/// <returns>当前时间，单位秒，精度微秒</returns>
static double  getCurrentTime()
{
	LARGE_INTEGER ticks, Frequency;
	QueryPerformanceFrequency(&Frequency);
	QueryPerformanceCounter(&ticks);
	return  (double)ticks.QuadPart / (double)Frequency.QuadPart;
}
/// <summary>
/// 性能测试
/// </summary>
static void test() {
	double d = getCurrentTime();
	loadStr(a, "50000");
	loadInt(b, 50000);
	for (int64_t i = 1; i <= 500000; i++) {
		plus(a, b, c);
	}
	printf("plus  performence   1: %llfs\n", getCurrentTime() - d);
	d = getCurrentTime();
	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	loadInt(b, 5);
	for (int64_t i = 1; i <= 500000; i++) {
		plus(a, b, c);
	}
	printf("plus  performence   2: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	loadStr(b, "11111111111111111111111111111111111111");
	for (int64_t i = 1; i <= 500000; i++) {
		plus(b, a, c);
	}
	printf("plus  performence   3: %llfs\n", getCurrentTime() - d);


	d = getCurrentTime();
	loadStr(a, "50000");
	loadInt(b, 50000);
	for (int64_t i = 1; i <= 500000; i++) {
		plusq(a, b);
	}
	printf("plusq performence   1: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	for (int64_t i = 500000000; i <= 500000000 + 500000; i++) {
		loadInt(b, i);
		plusq(a, b);
	}
	printf("plusq performence   2: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(b, "999999999999999999999999999999999999999999999999999999999999999999");
	for (int64_t i = 500000000; i <= 500000000 + 500000; i++) {
		loadInt(a, i);
		plusq(a, b);

	}
	printf("plusq performence   3: %llfs\n", getCurrentTime() - d);


	d = getCurrentTime();
	loadStr(a, "50000");
	loadInt(b, 10000);
	for (int64_t i = 1; i <= 500000; i++) {
		sub(a, b, c);
	}
	printf("sub   performence   1: %llfs\n", getCurrentTime() - d);



	d = getCurrentTime();
	loadStr(a, "100000000000000000000000000000000000000000000000000000000000000000");
	loadInt(b, 11111);
	for (int64_t i = 1; i <= 500000; i++) {
		sub(a, b, c);
	}
	printf("sub   performence   2: %llfs\n", getCurrentTime() - d);


	d = getCurrentTime();
	loadStr(a, "100000000000000000000000000000000000000000000000000000000000000000");
	loadStr(b, "11111111111111111111111111111111111111");
	for (int64_t i = 1; i <= 500000; i++) {
		sub(a, b, c);
	}
	printf("sub   performence   3: %llfs\n", getCurrentTime() - d);



	d = getCurrentTime();
	loadStr(a, "50000000000");
	loadInt(b, 500000);
	for (int64_t i = 1; i <= 500000; i++) {
		subq(a, b);
	}
	printf("subq  performence   1: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(a, "100000000000000000000000000000000000000000000000000000000000000000");
	loadInt(b, 11111);
	for (int64_t i = 1; i <= 500000; i++) {
		subq(a, b);
	}
	printf("subq  performence   2: %llfs\n", getCurrentTime() - d);


	
	d = getCurrentTime();
	loadStr(a, "100000000000000000000000000000000000000000000000000000000000000000");
	loadStr(b, "11111111111111111111111111111111111111");
	for (int64_t i = 1; i <= 500000; i++) {
		subq(a, b);
	}
	printf("subq  performence   3: %llfs\n", getCurrentTime() - d);


	d = getCurrentTime();
	loadStr(a, "50000");
	loadInt(b, 12345);
	for (int64_t i = 1; i <= 500000; i++) {
		mul(a, b, c);
	}
	printf("mul   performence   1: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	loadInt(b, 12345);
	for (int64_t i = 1; i <= 500000; i++) {
		mul(a, b, c);
	}
	printf("mul   performence   2: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	loadStr(b, "11111111111111111111111111111111111111");
	for (int64_t i = 1; i <= 500000; i++) {
		mul(b, a, c);
	}
	printf("mul   performence   3: %llfs\n", getCurrentTime() - d);


	d = getCurrentTime();
	loadStr(a, "2");
	loadInt(b, 2);
	for (int64_t i = 1; i <= 1000; i++) {
		mulq(a, b);
	}
	printf("mulq  performence   1: %llfs\n", getCurrentTime() - d);
	d = getCurrentTime();
	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	loadInt(b, 2);
	for (int64_t i = 1; i <= 1000; i++) {
		mulq(a, b);
	}
	printf("mulq  performence   2: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	loadStr(b, "11111111111111111111111111111111111111");
	for (int64_t i = 1; i <= 1000; i++) {
		mulq(b, a);
	}
	printf("mulq  performence   3: %llfs\n", getCurrentTime() - d);



	d = getCurrentTime();
	loadStr(a, "50000");
	loadInt(b, 12345);
	for (int64_t i = 1; i <= 500000; i++) {
		div(a, b, c, mod);
	}
	printf("div   performence   1: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(a, "100000000000000000000000000000000000000000000000000000000000000000");
	loadInt(b, 12345);
	for (int64_t i = 1; i <= 500000; i++) {
		div(a, b, c, NULL);
	}
	printf("div   performence   2: %llfs\n", getCurrentTime() - d);

	d = getCurrentTime();
	loadStr(a, "100000000000000000000000000000000000000000000000000000000000000000");
	loadStr(b, "11111111111111111111111111111111111111");
	for (int64_t i = 1; i <= 500000; i++) {
		div(a, b, c, mod);
	}
	printf("div   performence   3: %llfs\n", getCurrentTime() - d);



	loadStr(a, "1");
	loadStr(b, "2");
	for (int64_t i = 1; i <= 1000; i++) {
		mulq(a, b);
	}
	d = getCurrentTime();
	for (int64_t i = 1; i <= 1000; i++) {
		divq(a, b, mod);
	}
	printf("divq  performence   1: %llfs\n", getCurrentTime() - d);

	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	loadStr(b, "2");
	for (int64_t i = 1; i <= 1000; i++) {
		mulq(a, b);
	}
	d = getCurrentTime();
	for (int64_t i = 1; i <= 1000; i++) {
		divq(a, b, mod);
	}
	printf("divq  performence   2: %llfs\n", getCurrentTime() - d);



	loadStr(a, "999999999999999999999999999999999999999999999999999999999999999999");
	loadStr(b, "11111111111111111111111111111111111111");
	for (int64_t i = 1; i <= 500; i++) {
		mulq(a, b);
	}
	d = getCurrentTime();
	for (int64_t i = 1; i <= 500; i++) {
		divq(a, b, mod);
	}
	printf("divq  performence   3: %llfs\n", getCurrentTime() - d);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/187414.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

数学建模学习笔记（15）时间序列分析

数学建模学习笔记（15）时间序列分析

时间序列分析时间序列分析概述和数据预处理时间序列分解模型指数平滑模型ARIMA模型时间序列分析概述和数据预处理 时间序列的概念&#xff1a;也称为动态序列&#xff0c;是指将某种现象的指标值按照时间顺序排列而成的数值序列。 时间序列的组成要素&#xff1a;时间要素、数…
阅读更多...
表格控件Aspose.Cells for Java 授权须知

表格控件Aspose.Cells for Java 授权须知

Aspose API支持流行文件格式处理&#xff0c;并允许将各类文档导出或转换为固定布局文件格式和最常用的图像/多媒体格式。 Aspose.Cells for Java 是一个屡获殊荣的Excel电子表格处理API&#xff0c;它允许Java开发人员在自己的Java应用程序中嵌入可读取、写入和操作Excel电子…
阅读更多...
天云数据Hubble数据库被评为“IDC创新者：中国分布式数据库，2022”

天云数据Hubble数据库被评为“IDC创新者：中国分布式数据库，2022”

近日&#xff0c;国际知名研究机构 IDC 发布《IDC Innovator&#xff1a;中国分布式关系型数据库》报告正式发布&#xff0c;天云融创数据科技&#xff08;北京&#xff09;有限公司&#xff08;以下简称“天云数据”&#xff09;被评为“IDC创新者&#xff1a;中国分布式数据库…
阅读更多...
经过ASEMI整流桥MB10F后输出电压是多少

经过ASEMI整流桥MB10F后输出电压是多少

编辑-Z 型号&#xff1a;MB10F 封装&#xff1a;MBF-4 最大重复峰值反向电压&#xff08;VRRM&#xff09;&#xff1a;1000V 最大平均正向整流输出电流&#xff08;IF&#xff09;&#xff1a;1.0A 峰值正向浪涌电流&#xff08;IFSM&#xff09;&#xff1a;35A 每个元…
阅读更多...
清楚姐姐玩翻翻乐[期望dp]

清楚姐姐玩翻翻乐[期望dp]

首先这肯定是个期望dp。 首先明确二点 1.一旦这张牌已经知道数字了&#xff0c;下次翻他肯定是给他配对 2.如果已经知道了两张相同数字的卡片&#xff0c;那么在之后什么时候翻面都不会影响操作次数 故dp状态只需要记录只知道一张的卡片数量和未知的卡片数量。 接下来一个问题就…
阅读更多...
多微网优化调度（风机、光伏、蓄电池、燃料电池、柴油机、电网交互）（Matlab代码实现）

多微网优化调度（风机、光伏、蓄电池、燃料电池、柴油机、电网交互）（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
【c语言进阶】文件操作（上）

【c语言进阶】文件操作（上）

&#x1f680;write in front&#x1f680; &#x1f4dc;所属专栏&#xff1a;> c语言学习 &#x1f6f0;️博客主页&#xff1a;睿睿的博客主页 &#x1f6f0;️代码仓库&#xff1a;&#x1f389;VS2022_C语言仓库 &#x1f3a1;您的点赞、关注、收藏、评论&#xff0c;是…
阅读更多...
【C++11新特性】| 并发编程

【C++11新特性】| 并发编程

文章目录一、std::thread1.1 成员函数1.2 案例二、std::mutex三、std::lock3.1 lock_guard3.2 unique_lock3.3 lock_guard与unique_lock的对比四、std::atomic五、volatile六、condition_variable成员函数七、future、promise、packaged_task7.1 std::promise7.2 std::future7.…
阅读更多...
【Cloudcone】VPS 登录、防火墙设置

【Cloudcone】VPS 登录、防火墙设置

服务器登录、防火墙设置本来是一件很简单的事情&#xff0c;但是我买了国外服务器&#xff0c;有些地方出现了一些问题。 文章目录一、简介二、使用ipv6登录服务器三、防火墙设置四、小插曲一、简介 我一直用的腾讯云的服务器&#xff0c;但是带宽太低了&#xff0c;只有4M。最…
阅读更多...
2023年二月份图形化三级打卡试题

2023年二月份图形化三级打卡试题

活动时间 从2023年 2月1日至1月21日&#xff0c;每天一道编程题。 本次打卡的规则如下&#xff1a; &#xff08;1&#xff09;小朋友每天利用10~15分钟做一道编程题&#xff0c;遇到问题就来群内讨论&#xff0c;我来给大家答疑。 &#xff08;2&#xff09;小朋友做完题目后&…
阅读更多...
CSS第四章——文本属性

CSS第四章——文本属性

文章目录4.1 文本颜色4.2 对齐文本4.3 装饰文本4.4 文本缩进4.5 行间距一些学习笔记。 CSS Text&#xff08;文本&#xff09;属性可定义文本的外观&#xff0c;比如文本的颜色、对齐文本、装饰文本、文本缩进、行间距等。 属性表示注意点color文本颜色通常使用十六进制 而且…
阅读更多...
【算法题解】13. 删除链表的倒数第 N 个结点

【算法题解】13. 删除链表的倒数第 N 个结点

文章目录题目解法一&#xff1a;计算链表长度Java 代码实现Go 代码实现复杂度分析解法二&#xff1a;双指针Java 代码实现Go 代码实现复杂度分析这是一道 中等难度 的题。 题目来自&#xff1a;https://leetcode.cn/problems/remove-nth-node-from-end-of-list/description/ 题…
阅读更多...
numpy快速交换行列

numpy快速交换行列

import numpy as np “”" 快速加换两行两列 “”" #交换两列第一列跟第三列 v1np.arange(100) v2v1.reshape((20,5)) v3v2[:,[0,3,2,1,4]] print(v3) “”" 快速交换两列 第一列跟第三列 “”" print() mask list(range(5))#生成一个0到4的列表 #快速…
阅读更多...
[iHooya]2023年1月30日作业解析

[iHooya]2023年1月30日作业解析

温度统计 现有一段时间的温度数据&#xff0c;请统计指定温度出现的次数。 输入 第一行一个整数n,表示温度数据的个数。&#xff08;0 < n ≤ 200&#xff09; 第二行n个整数&#xff0c;以空格分隔&#xff0c;每个整数表示一个温度&#xff0c;温度的范围大于等于0&#…
阅读更多...
OpenCV实战（9）——基于反向投影直方图检测图像内容

OpenCV实战（9）——基于反向投影直方图检测图像内容

OpenCV实战&#xff08;9&#xff09;——基于反向投影直方图检测图像内容0. 前言1 反向投影直方图2. 反向投影颜色直方图3. 完整代码小结系列链接0. 前言 直方图是图像内容的一个重要特征。如果查看显示特定纹理或特定对象的图像区域&#xff0c;则该区域的直方图可以看作是一…
阅读更多...
计算机网络之TCP全连接队列与半连接队列

计算机网络之TCP全连接队列与半连接队列

什么是全、半连接队列 服务端接收syn请求后&#xff0c;内核会把该连接放入到半连接队列&#xff0c;服务端对synack返回ack后&#xff0c;会把连接从半连接队列移除&#xff0c;创建新的全连接&#xff0c;并把新的连接放入全连接队列 查看全连接队列的命令 全连接队列满了…
阅读更多...
Deep Learning Tuning Playbook（深度学习调参手册中译版）

Deep Learning Tuning Playbook（深度学习调参手册中译版）

前言 由五名研究人员和工程师组成的团队发布了《Deep Learning Tuning Playbook》&#xff0c;来自他们自己训练神经网络的实验结果以及工程师的一些实践建议&#xff0c;目前在Github上已有1.5k星。原项目地址本文为《Deep Learning Tuning Playbook》中文翻译版本&#xff0…
阅读更多...
聊一聊微信小程序生命周期你最想知道的一些事

聊一聊微信小程序生命周期你最想知道的一些事

目录 前言 解析 运行机制 总结 前言 &#xff08;1&#xff09;为什么是微信小程序 最近有人问我一些关于微信小程序的问题&#xff0c;今天有时间也就整理了一些微信小程序的相关资料&#xff0c;给大家简单系统总结一些微信小程序的相关知识及生命周期。 &#xff08;2…
阅读更多...
使用光泵磁力仪（OPMs）非接触测量视网膜活动

使用光泵磁力仪（OPMs）非接触测量视网膜活动

使用光泵磁力仪&#xff08;OPMs&#xff09;非接触测量视网膜活动摘要绪论方法2.1参与者和测量设置2.2刺激2.3数据分析结果讨论原文见&#xff1a; https://www.sciencedirect.com/science/article/pii/S1053811921008016 摘要 光泵磁力仪&#xff08;OPM&#xff09;已被用…
阅读更多...
关于提升销量和排名，亚马逊、wish、ebay卖家该怎么做？

关于提升销量和排名，亚马逊、wish、ebay卖家该怎么做？

新年好&#xff0c;我是龙哥测评&#xff0c;在这里祝愿所有跨境朋友在新的一年里财源滚滚&#xff0c;一切顺利。 接下来龙哥就来说说&#xff0c;为什么店铺销量提升不上去&#xff0c;产品曝光低转化率低&#xff0c;产品有排名但是没销量&#xff0c;等等这些问题&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023