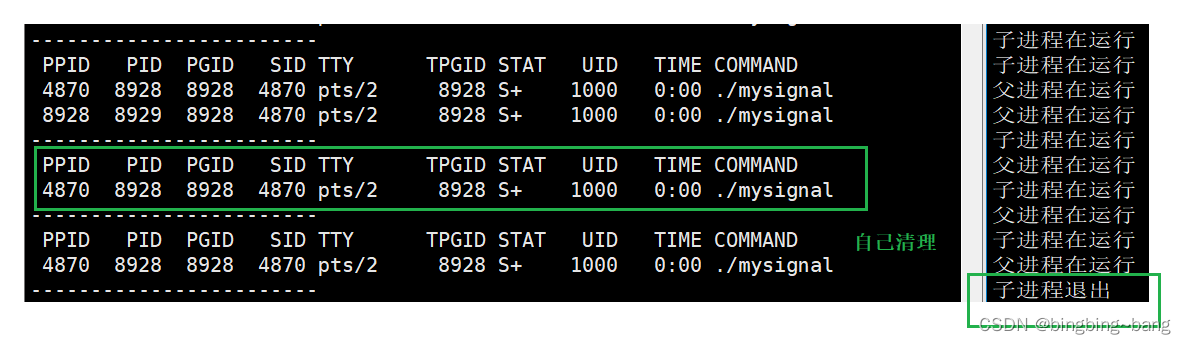
首先这肯定是个期望dp。
首先明确二点
1.一旦这张牌已经知道数字了，下次翻他肯定是给他配对
2.如果已经知道了两张相同数字的卡片，那么在之后什么时候翻面都不会影响操作次数
故dp状态只需要记录只知道一张的卡片数量和未知的卡片数量。
接下来一个问题就是对于一个状态，他的最优操作是什么？
首先凭感觉我们可以知道，当未知的牌数量很多的时候，翻两张比较优秀。因为通过基本的概率论计算我们可以知道翻一张知道点数和一张未知点数的卡片，两者相同的概率只有
$$\frac{1}{(知道一张的卡片数量)\times (未知卡片数量)}$$
是一个非常小的值，如果失败则不如翻两张未知的。
接下来我们手动模拟一下小样例的情况：
首先模拟1张已知1张未知，毫无疑问只需要一次操作。
首先模拟1张已知3张未知，通过简单的计算我们可以得到翻两张未知更加优秀，同时通过计算过程我们可以发现未知牌数增多会增加翻"一张已知一张未知“的操作次数期望。
然后模拟2张已知2张未知，通过计算我们发现第一次操作翻一张已知一张未知更加优秀（在这里你可能会很失望，感觉找不出规律了）。
然后模拟2张已知4张未知，通过简单的计算我们可以得到翻两张未知更加优秀。
最后模拟3张已知3张未知同样的我们第一步得到翻两张未知更加优秀。
好，振奋人心！其余的情况我们可以通过单调性来得到
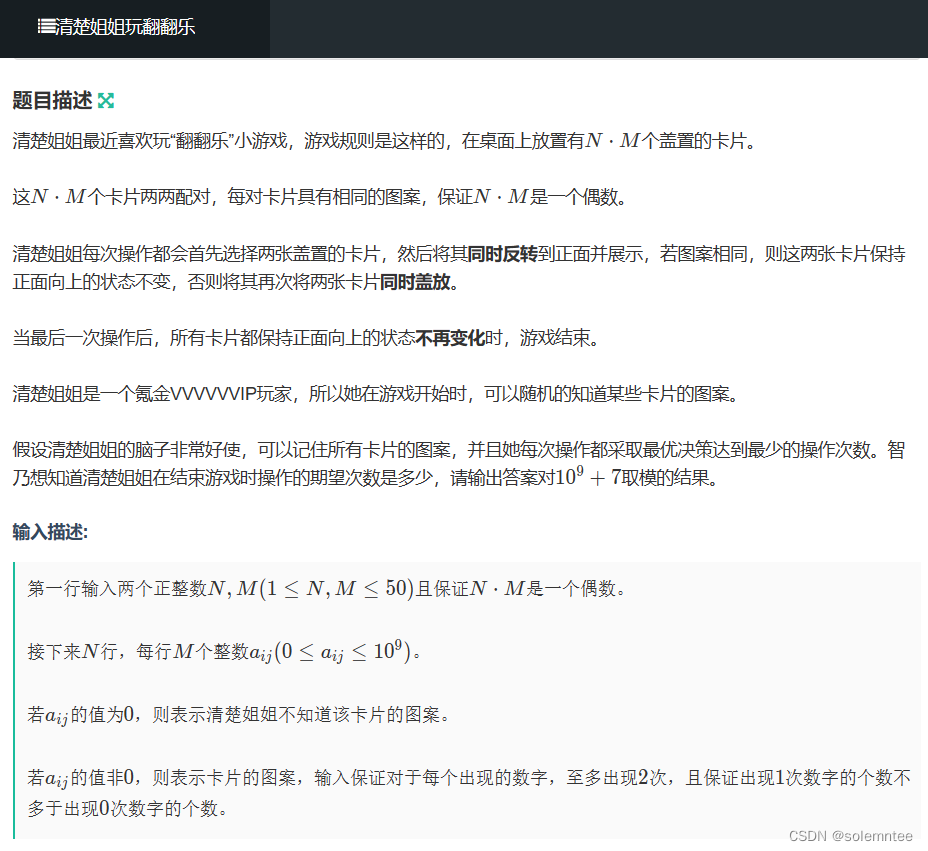
经过探索我们发现，除了(1,1),(2,2)这两种特殊情况的最优操作比较奇怪以外，另外的状态就直接无脑翻两张未知就可以了。good！那让我们来仔细的分类讨论一下（这是我的草稿纸展示捏）

一共有四种情况，这里我们记已经知道数字（但是反面）的牌的数量是$k$(know)，不知道数字的牌的数量是$dk$(don’t know)（谁能不夸我英语好）
我们翻了两张未知的各个情况的概率
一、两张未知的牌都是没有出现过的数字但是恰好他们的点数一样

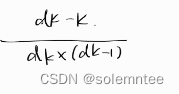
二、两张未知的牌都是没有出现过的数字但是他们的点数不一样

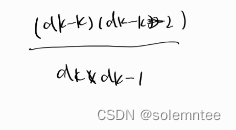
三、一张是已经出现过的数字，一张是没有出现过的数字

四、两张未知的牌都是出现过的数字

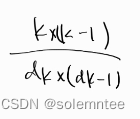
那么转移就很简单啦，我们记录这四个概率为$p_1,p_2,p_3,p_4$
$$\begin{gathered} d{p}_{k,dk}=p_1\times (1+d{p}_{k,dk-2}) \\ +p_2\times (1+d{p}_{k+2,dk-2}) \\ +p_3\times (2+d{p}_{k,dk-2}) \\ +p_4\times (3+d{p}_{k-2,dk-2}) \end{gathered}$$
注意上文讨论过的(1,1)=1和(2,2)=5/2的特殊转移哦

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int mod=1e9+7;
ll poww(ll a,ll b){
    ll t=1;
    while(b){
        if(b&1)t=t*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return t;
}
void add(int &a,int b){
    a+=b;
    if(a>=mod)a-=mod;
}
void del(int &a,int b){
    a-=b;
    if(a<0)a+=mod;
}
int dp[2505][2505];
int dfs(int k,int dk){
    if(dp[k][dk]!=-1)return dp[k][dk];
    if(k==1&&dk==1)return dp[k][dk]=1;
    if(k==2&&dk==2){
        dp[k][dk]=1ll*5*poww(2,mod-2)%mod;
        return dp[k][dk];
    }
    dp[k][dk]=0;
    int tk,tdk;
    ///两个未知一样
    tk=k,tdk=dk-2;
    if(tk>=0&&tdk>=0&&tdk>=tk&&(tdk-tk)%2==0){
        add(dp[k][dk],1ll*(1+dfs(tk,tdk))%mod*(dk-k)%mod*poww(dk*(dk-1),mod-2)%mod);
    }
    ///两个未知不一样
    tk=k+2,tdk=dk-2;
    if(tk>=0&&tdk>=0&&tdk>=tk&&(tdk-tk)%2==0){
        add(dp[k][dk],1ll*(1+dfs(tk,tdk))%mod*(dk-k)%mod*(dk-k-2)%mod*poww(dk*(dk-1),mod-2)%mod);
    }
    ///一个未知
    tk=k,tdk=dk-2;
    if(tk>=0&&tdk>=0&&tdk>=tk&&(tdk-tk)%2==0){
        add(dp[k][dk],1ll*(2+dfs(tk,tdk))%mod*(dk-k)%mod*2%mod*k%mod*poww(dk*(dk-1),mod-2)%mod);
    }
    ///两个已知
    tk=k-2,tdk=dk-2;
    if(tk>=0&&tdk>=0&&tdk>=tk&&(tdk-tk)%2==0){
        add(dp[k][dk],1ll*(3+dfs(tk,tdk))%mod*k%mod*(k-1)%mod*poww(dk*(dk-1),mod-2)%mod);

    }
    //printf("%d %d %d\n",k,dk,dp[k][dk]);
    return dp[k][dk];
}
int main()
{
    //init(200000);
    memset(dp,-1,sizeof(dp));
    int n,m;
    scanf("%d%d",&n,&m);
    unordered_map<int,int>mp;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            int t;
            scanf("%d",&t);
            if(t!=0)mp[t]++;
        }
    }
    int cnt1=0,cnt2=0;
    for(auto [fi,se]:mp){
        if(se==1)cnt1++;
        else cnt2++;
    }
    printf("%d",(cnt2+dfs(cnt1,n*m-cnt2*2-cnt1))%mod);
    return 0;
}
/*
5 2
0 0 1 0 0
*/