时间序列分析概述和数据预处理

时间序列的概念：也称为动态序列，是指将某种现象的指标值按照时间顺序排列而成的数值序列。

时间序列的组成要素：时间要素、数值要素。

时间序列的分类：

• 时期时间序列：数值要素反应现象在一定时期内的发展的结果；
• 时点时间序列：数值要素反映现象在一定时间点上的瞬间水平。

备注：时期序列可以累积相加，时点序列不能相加。因此后面的灰色预测模型只能用于时期时间序列。

时间序列分析的内容：时间序列分析可以分为描述过去、分析规律和预测未来三个部分。

数据预处理（去除缺失值）：缺失值处理是时间序列分析模型的基本预处理。

• 缺失值处理方法：缺失值发生在时间序列的头部或尾部，则采用直接删除的方法；缺失值发生在序列的中间位置，则不能删除，可以采用缺失值替换的方法。
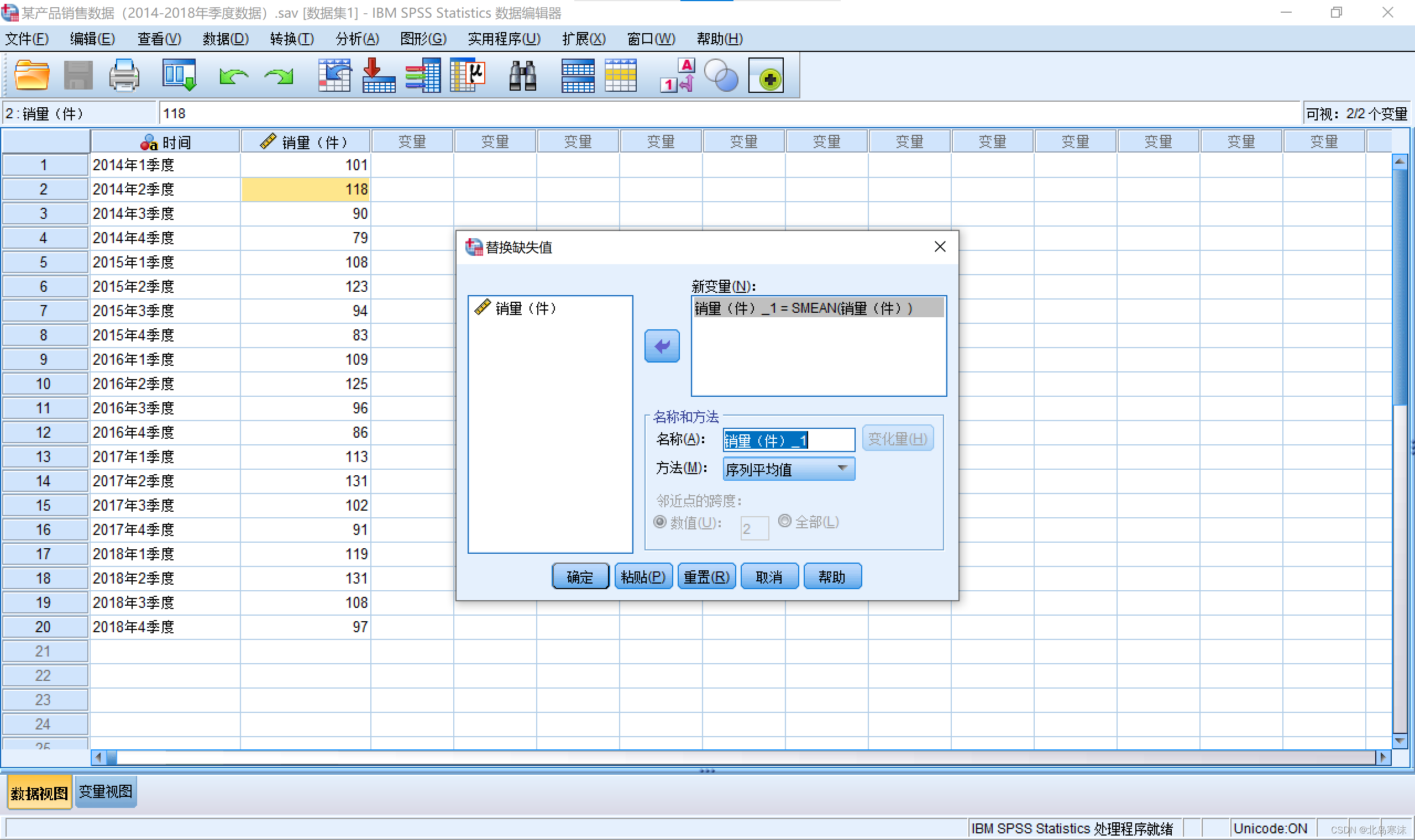
• SPSS提供五种替换缺失值的方法：序列平均值；临近点的平均值；临近点的中位数；线性插值；临近点的线性趋势。
• SPSS进行数据缺失值预处理：

1.打开SPSS软件并导入数据，依次点击：转换→替换缺失值

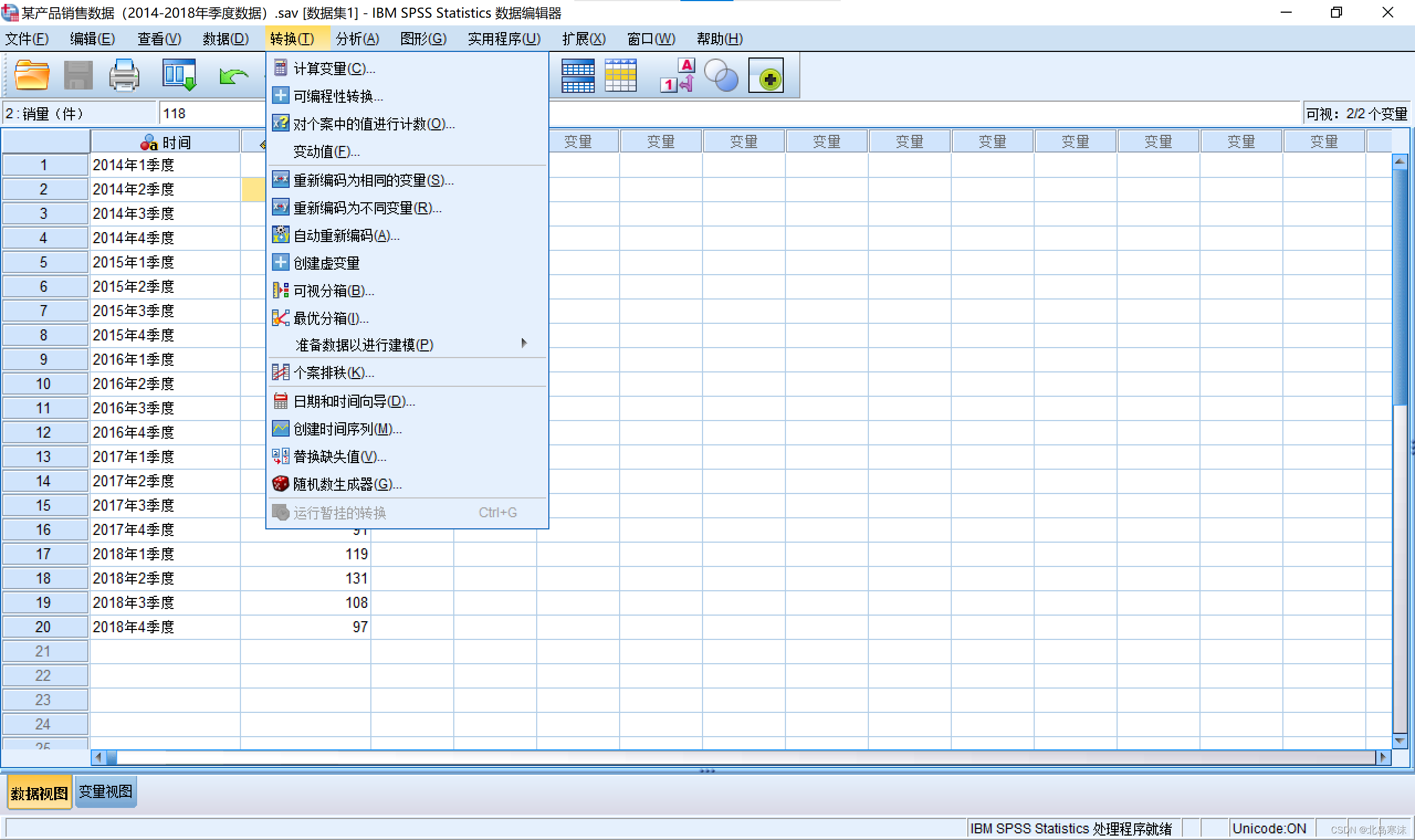
2.选择需要替换缺失值的变量，指定新的变量的名称和替换缺失值的方法。

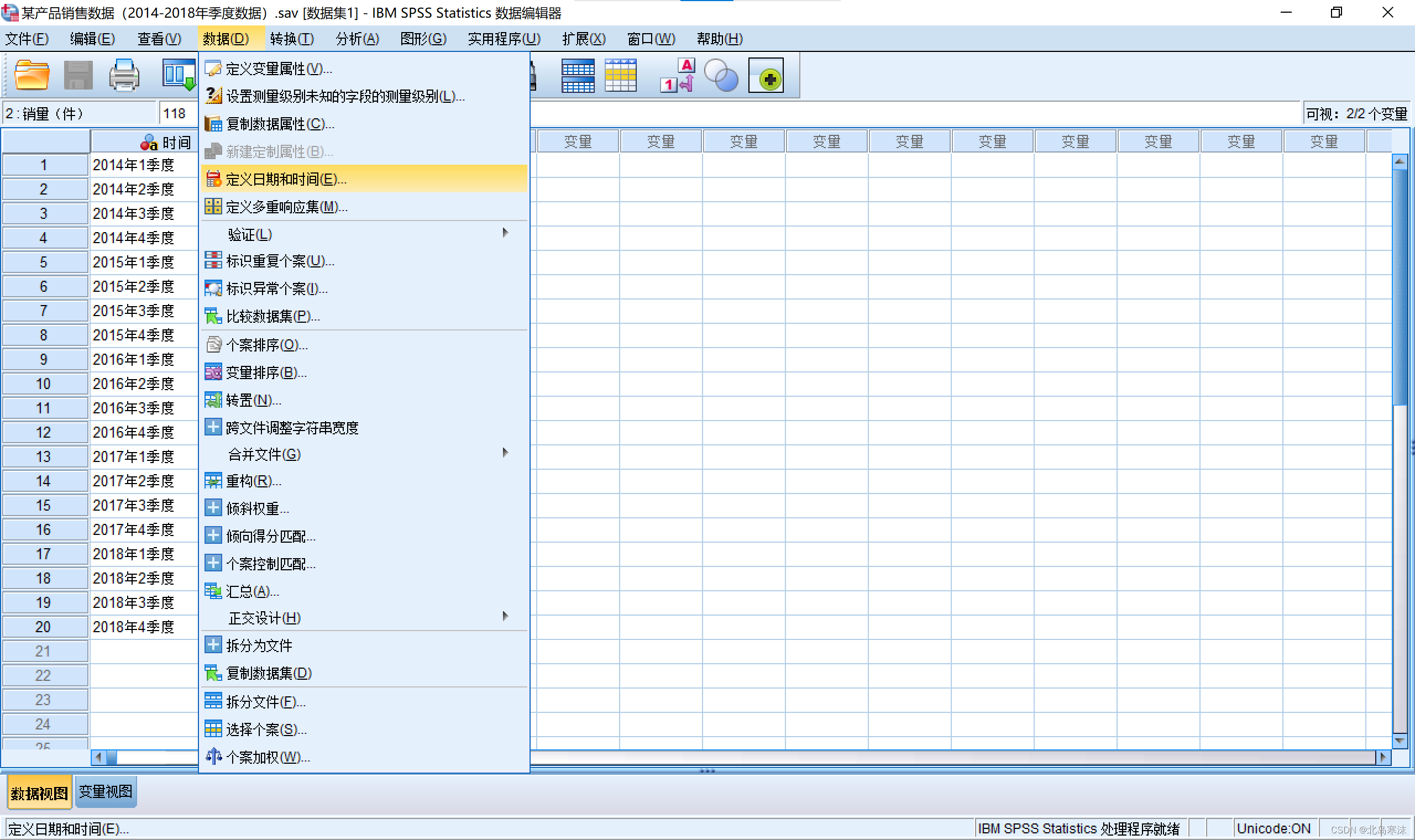
数据预处理（定义时间变量）：需要指定哪一个属性是时间变量避免出错。

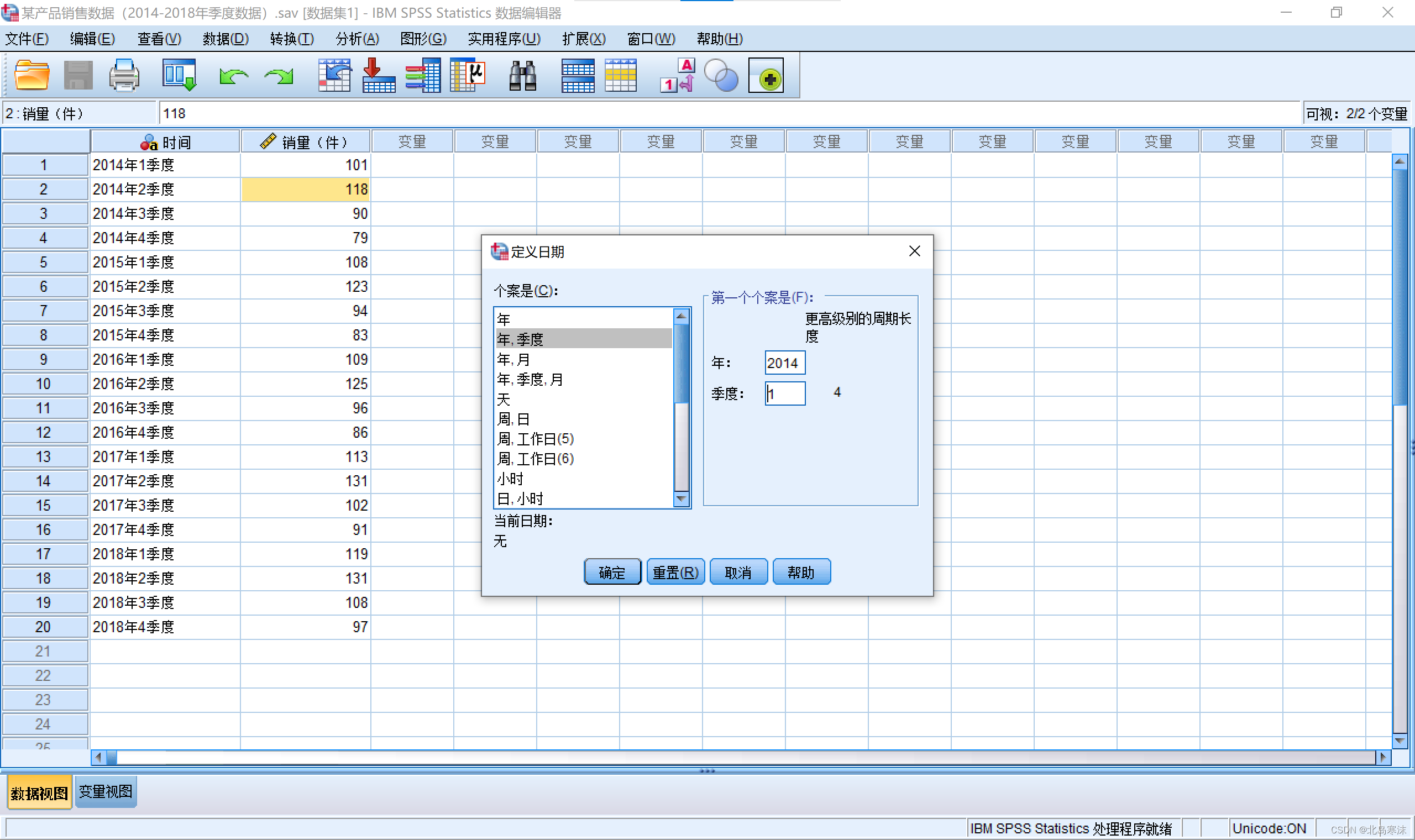
1. 打开导入了数据的SPSS软件，依次点击：数据→定义日期和时间
   
2. 选择个案类型并指定起始时间。
   

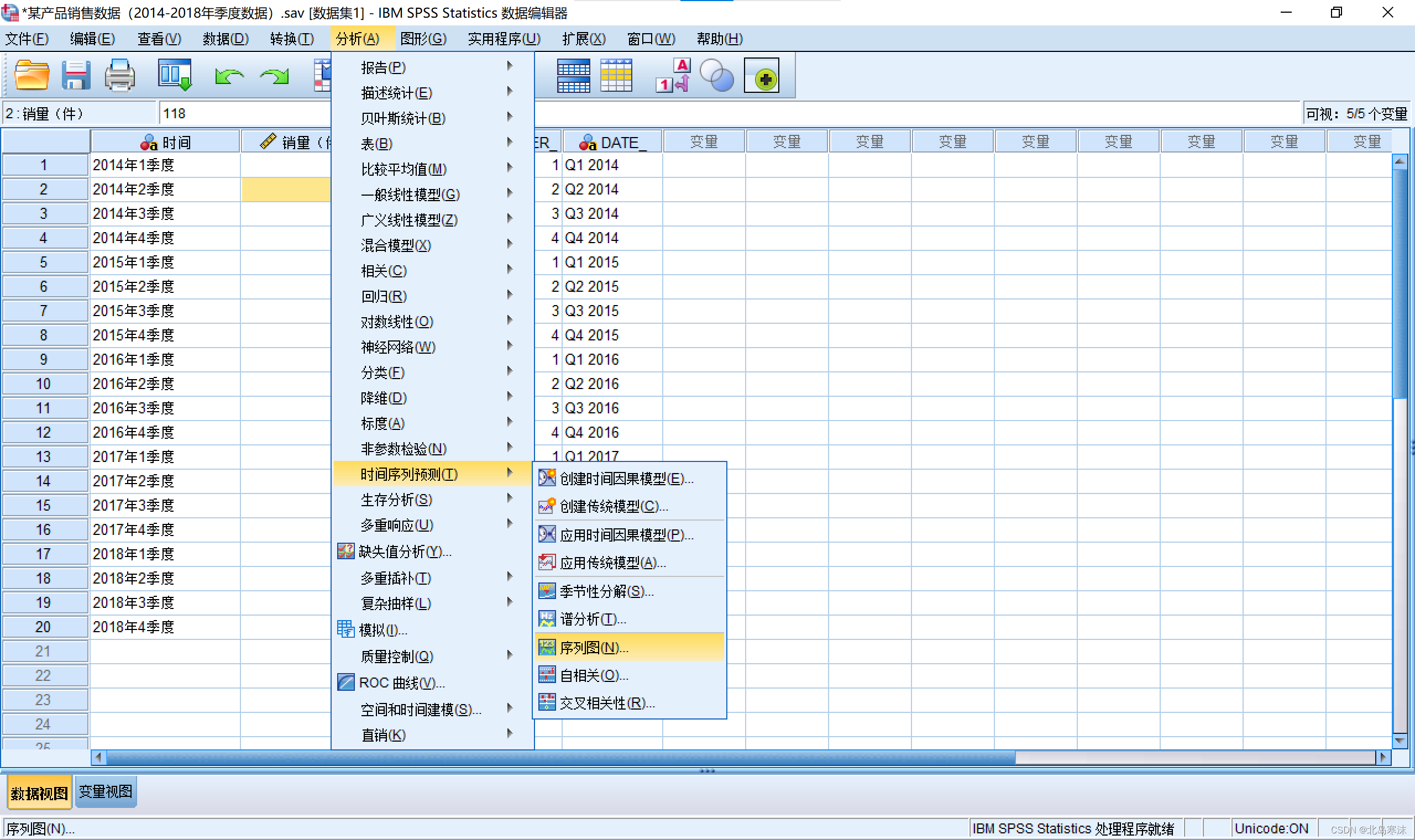
SPSS绘制时间序列图：

1. 依次点击：分析→时间序列预测→序列图
   
   2.选择时间变量和因变量。
   
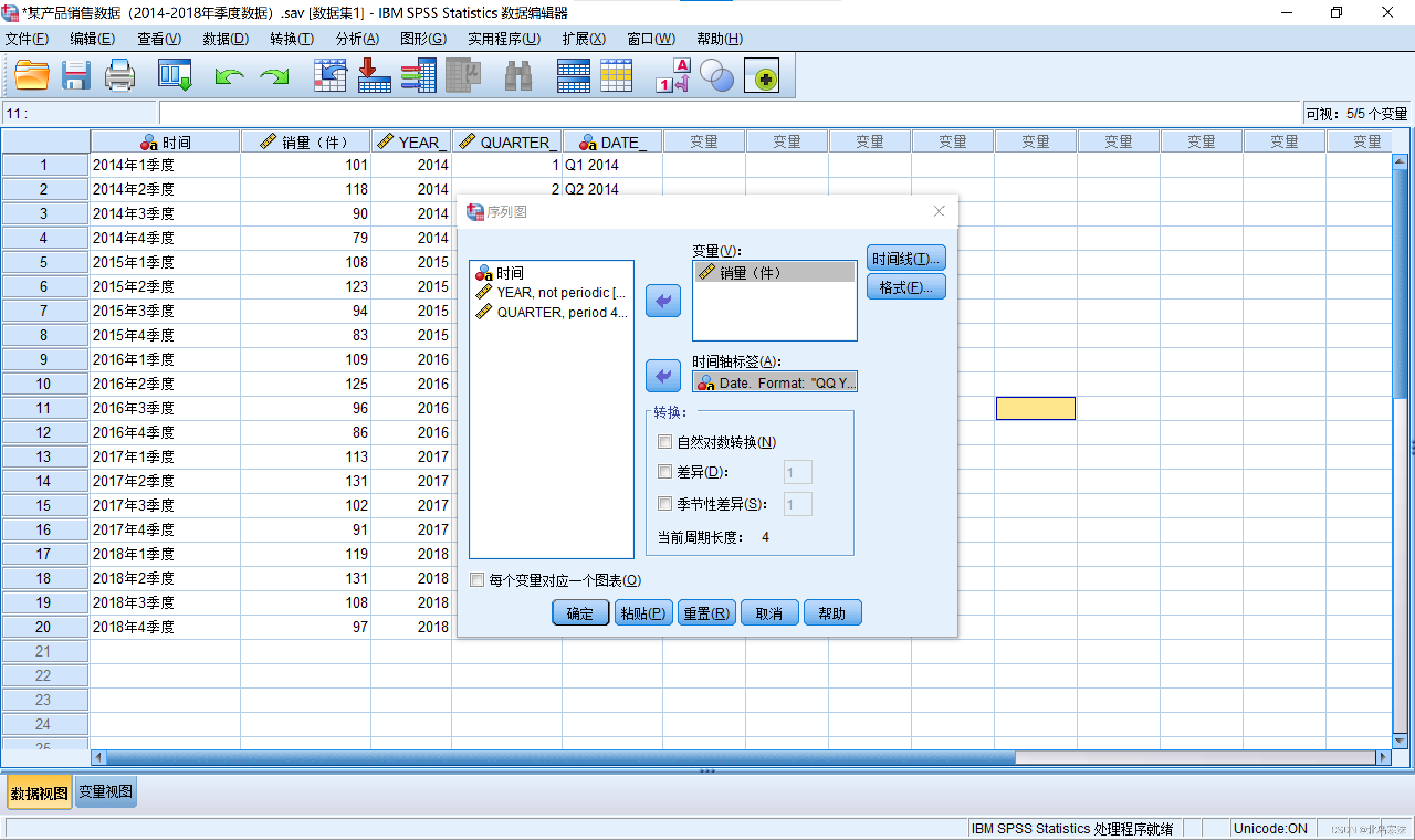
   绘制完成的图片可以双击进去进行相关的优化。

时间序列分解模型

时间序列分解的前提：数据具有周期性才能使用时间序列分解，也就是说年份数据不能使用时间序列分解模型。

时间序列的分解元素：

• 长期变动趋势（T）：统计指标在相当长的一段时间内，受到长期趋势影响因素的影响，表现出持续上升或持续下降的趋势。
• 季节趋势（S）：由于季节的转变使得指标数值发生周期性变动。这里的季节是广义的，一般以月、季、周为时间单位，不能以年作为单位。
• 循环变动（C）：与季节变动的周期不同，往往以若干年为一个周期，在曲线图上表现为波浪式的周期变动。
• 不规则变动（I）：由于某些随机因素导致的数值变化，这些因素的作用是不可预知且没有规律性的，可以视为由于众多偶然因素对时间序列造成的影响，也就是回归中的扰动项。

以上四种变动就是时间序列数值变化的分解结果。有时这些变动会同时出现在一个时间序列中，但是有时候也可能只出现一种或几种。

叠加模型和乘积模型：

• 使用情况：如果四种变动是相互独立的关系，就应该使用叠加模型；如果存在相互影响，则应该使用乘积模型。
• 推荐使用：如果在时间序列图上，随着事件的推移，序列的季节波动越来越大，则建议使用乘积模型；如果季节波动保持稳定，则建议使用叠加模型。当不存在季节波动时则两种分解都可以。

SPSS进行时间序列分解：

• 依次点击：分析→时间序列预测→季节性分解
  
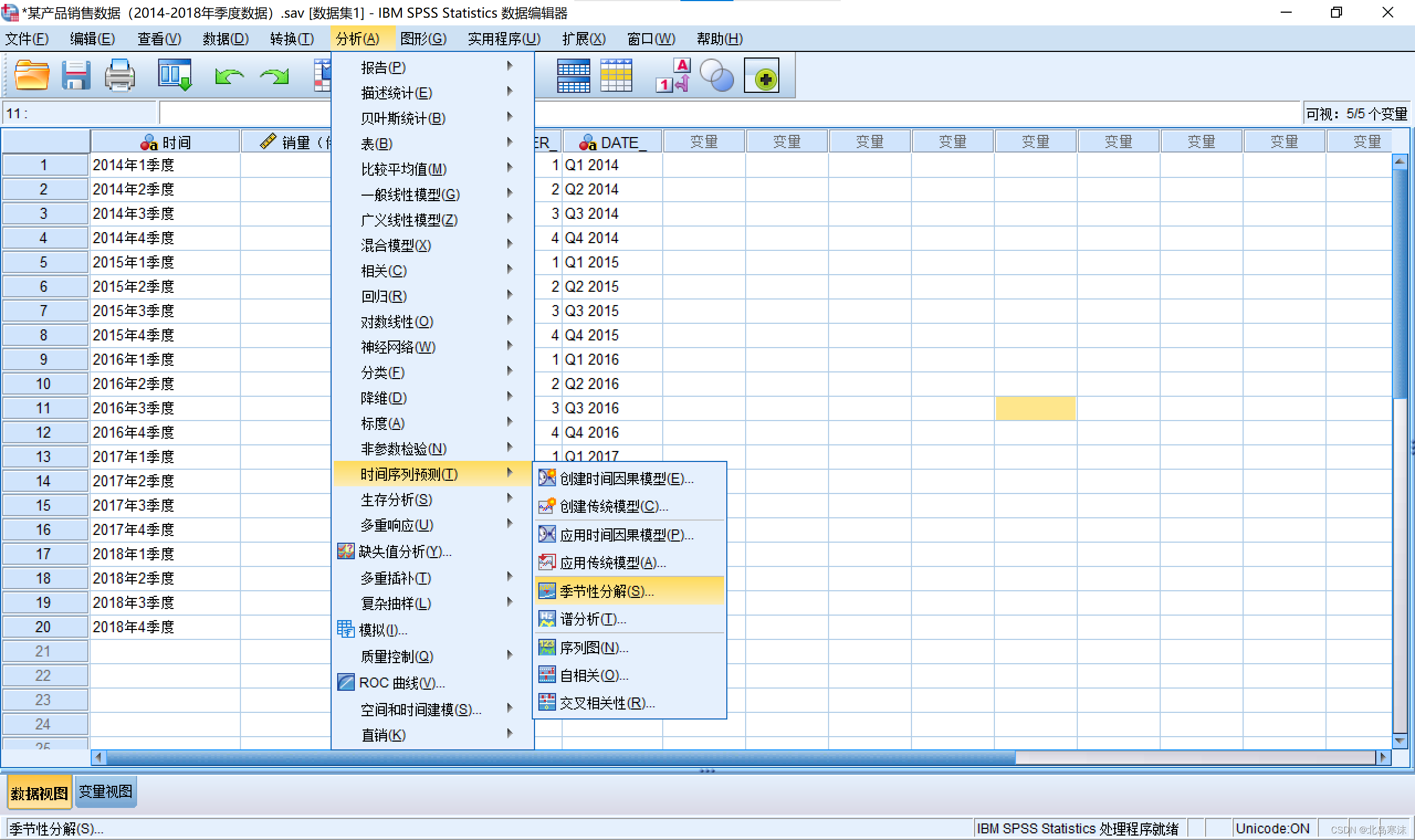
  2.选择需要进行时间序列分解的变量，指定模型是叠加还是乘积。如果周期长度为奇数则选择所有点相等，为偶数则选择端点按0.5加权。
  

SPSS时间序列分析结果：

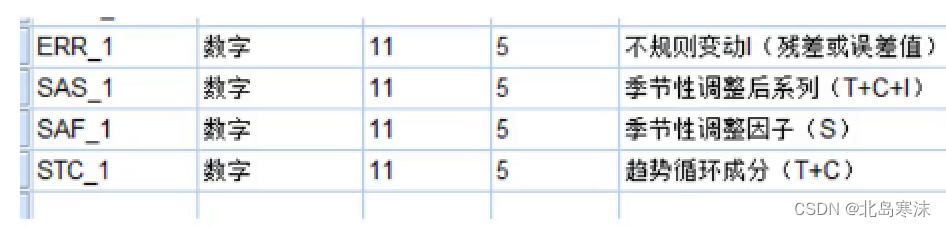
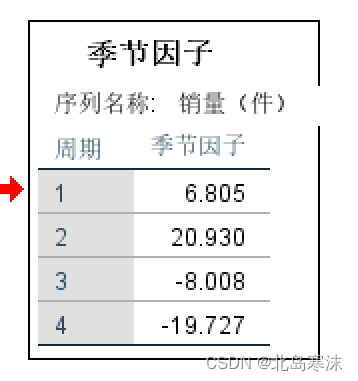
结果解释：

• 叠加模型：每一个季节的季节因子表示该季节的指标超过全年平均指标的水准。如果大于零则表示高于全年平均指标，小于零则表示低于全年平均指标。
• 乘法模型：每一个季节的季节因子表示该季节的指标为全年平均指标的多少倍。如果大于一则表示高于全年平均指标，小于一则表示低于全年平均指标。

如何使用结果进行预测：将预测结果变量中的季节性调整后序列加上季节因子，得到一个新的变量序列，对该序列进行拟合即可使用拟合函数进行预测。

SPSS专家建模器：从指数平滑模型和ARIMA模型中找出最合适的拟合模型。

指数平滑模型

简单指数平滑模型：

• 适用情况：适用于不含趋势和季节成分的时间序列。
• 预测原理：每一个平滑后的数据都是由过去的数据加权求和后所得，越接近当期的数据权重越大。
• 模型不足：简单指数平滑模型只能进行一期的预测。

霍特线性趋势模型：

• 适用条件：线性趋势，不含有季节成分。
• 预测原理：有两个平滑方程（水平平滑方程和趋势平滑方程）和一个预测方程。

布朗线性趋势模型：霍特线性趋势模型的一个特例，认为模型中的水平平滑参数和趋势平滑参数相等。

阻尼趋势模型：

• 适用情况：线性趋势逐渐减弱且不含有季节成分。
• 模型原理：在霍特线性趋势模型的基础上进行延伸。霍特线性趋势模型对长期预测往往过高，阻尼线性趋势模型缓解了较高的线性趋势。

简单季节性模型：适用于含有稳定的季节成分，不含有趋势。

温特加法模型：适用于含有线性趋势和稳定的季节成分。

温特乘法模型：适用于含有线性趋势和不稳定的季节成分。

ARIMA模型

平稳时间序列：

• 平稳时间序列的优点：平稳的时间序列是最容易处理的时间序列。
• 平稳的时间序列需要满足的三个条件：均值为固定常数；方差存在且为常数；协方差只与间隔有关，与时间点无关；
• 平稳性检验：一般，可以通过观察时序图来判断时间序列是否平稳，也可以通过假设检验的方法来进行判断。

备注：上述的要求称为协方差平稳，也称为弱平稳另外还有一种严格平稳，要求太高，因此时间序列中没有特殊说明则默认为弱平稳。

• 白噪声序列：均值为0的弱平稳时间序列就称为白噪声序列，因此白噪声序列是一种特殊的平稳时间序列。一般时间序列中的扰动项就被视为白噪声序列。

差分方程：

• 定义：将某个时间序列变量表示为该变量的滞后项、时间和其他变量的函数，这样的一个函数方程就被称为差分方程。
• 差分方程的齐次部分：只包含该变量自身和它的滞后项的计算式。
• 滞后算子：一种方便的表示方法。

将差分方程的齐次部分转化为特征方程，特征方程有p个解，这p个解的模长的大小决定了形为ARMA(p,q)模型的因变量序列是否平稳。

P阶自回归模型（AR模型）：

• 模型结构：将自身的滞后项作为自变量进行回归分析。
• 适用情况：自回归只能用于预测与自身前期相关的经济现象，也就是受到历史因素影响较大的经济现象。对于受到社会因素影响较大的经济现象不适合采用自回归。
• 注意事项：这里讨论的AR模型一定是平稳的时间序列模型，如果原始序列不平稳也要先转换为平稳的序列后才能进行建模。

备注：AR模型有专门用于判断平稳性的算法。对于一些不平稳的模型可以通过差分的方法转化为平稳的时间序列。

移动平均模型（MA模型）：

• 模型平稳性：可以证明MA(q)模型只要q是常数，则该模型一定是平稳的。
• 与AR模型的关系：为了简化AR模型参数估计的工作量可以引入MA模型，使得模型中的参数可以尽可能少。

自回归移动平均模型（ARMA模型）：

• 模型原理：设法将自回归过程和移动平均过程结合起来。
• 模型平稳性：平稳性只与自回归AR部分有关。
• 模型难点：很难正确地识别ARMA模型的阶数。
• 模型参数求解：ARMA模型目前最常用的参数估计方法是极大似然估计法。

模型完全性检验：
时间序列模型估计完成后需要对残差进行白噪声检验。如果残差是白噪声，则说明我们选择的模型能完全识别出时间序列数据的规律，所以模型可以接受；如果残差不是白噪声，则说明还有部分信息没有被识别利用，需要修正模型来识别这一部分信息。
SPSS中会自动算出P值，如果P值小于0.05则拒绝原假设，此时模型没有识别完全，需要进行修正。

ARIMA模型：差分自回归移动平均模型。首先对原始时间序列分解进行差分使得其变得平稳，然后再适用ARMA模型求解。

SARIMA模型：在ARIMA模型中包含额外的季节性项生成的模型。